Controlling Epidemic Spread using Probabilistic Diffusion Models on Networks

The spread of an epidemic is often modeled by an SIR random process on a social network graph. The MinINF problem for optimal social distancing involves minimizing the expected number of infections, when we are allowed to break at most $B$ edges; similarly the MinINFNode problem involves removing at most $B$ vertices. These are fundamental problems in epidemiology and network science. While a number of heuristics have been considered, the complexity of these problems remains generally open. In this paper, we present two bicriteria approximation algorithms for MinINF, which give the first non-trivial approximations for this problem. The first is based on the cut sparsification result of Karger \cite{karger:mathor99}, and works when the transmission probabilities are not too small. The second is a Sample Average Approximation (SAA) based algorithm, which we analyze for the Chung-Lu random graph model. We also extend some of our results to tackle the MinINFNode problem.

Deploying Vaccine Distribution Sites for Improved Accessibility and Equity to Support Pandemic Response

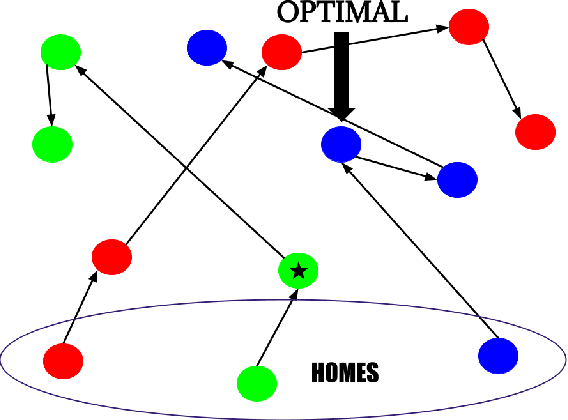
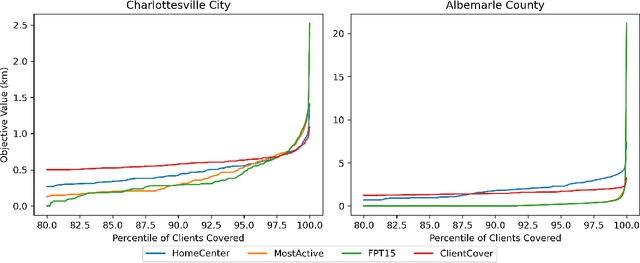
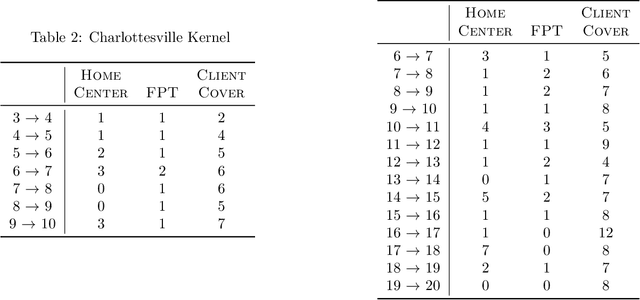
In response to COVID-19, many countries have mandated social distancing and banned large group gatherings in order to slow down the spread of SARS-CoV-2. These social interventions along with vaccines remain the best way forward to reduce the spread of SARS CoV-2. In order to increase vaccine accessibility, states such as Virginia have deployed mobile vaccination centers to distribute vaccines across the state. When choosing where to place these sites, there are two important factors to take into account: accessibility and equity. We formulate a combinatorial problem that captures these factors and then develop efficient algorithms with theoretical guarantees on both of these aspects. Furthermore, we study the inherent hardness of the problem, and demonstrate strong impossibility results. Finally, we run computational experiments on real-world data to show the efficacy of our methods.

Rawlsian Fairness in Online Bipartite Matching: Two-sided, Group, and Individual

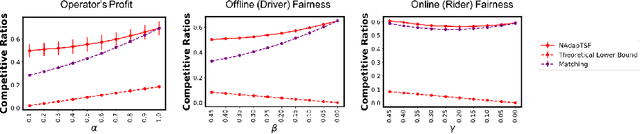
Online bipartite-matching platforms are ubiquitous and find applications in important areas such as crowdsourcing and ridesharing. In the most general form, the platform consists of three entities: two sides to be matched and a platform operator that decides the matching. The design of algorithms for such platforms has traditionally focused on the operator's (expected) profit. Recent reports have shown that certain demographic groups may receive less favorable treatment under pure profit maximization. As a result, a collection of online matching algorithms have been developed that give a fair treatment guarantee for one side of the market at the expense of a drop in the operator's profit. In this paper, we generalize the existing work to offer fair treatment guarantees to both sides of the market simultaneously, at a calculated worst case drop to operator profit. We consider group and individual Rawlsian fairness criteria. Moreover, our algorithms have theoretical guarantees and have adjustable parameters that can be tuned as desired to balance the trade-off between the utilities of the three sides. We also derive hardness results that give clear upper bounds over the performance of any algorithm.

Planning to Fairly Allocate: Probabilistic Fairness in the Restless Bandit Setting

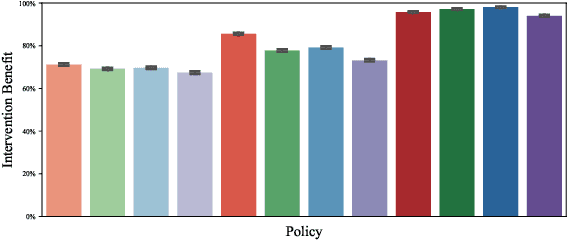
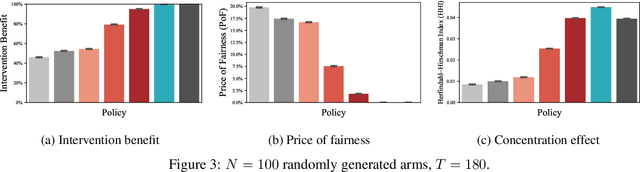
Restless and collapsing bandits are commonly used to model constrained resource allocation in settings featuring arms with action-dependent transition probabilities, such as allocating health interventions among patients [Whittle, 1988; Mate et al., 2020]. However, state-of-the-art Whittle-index-based approaches to this planning problem either do not consider fairness among arms, or incentivize fairness without guaranteeing it [Mate et al., 2021]. Additionally, their optimality guarantees only apply when arms are indexable and threshold-optimal. We demonstrate that the incorporation of hard fairness constraints necessitates the coupling of arms, which undermines the tractability, and by extension, indexability of the problem. We then introduce ProbFair, a probabilistically fair stationary policy that maximizes total expected reward and satisfies the budget constraint, while ensuring a strictly positive lower bound on the probability of being pulled at each timestep. We evaluate our algorithm on a real-world application, where interventions support continuous positive airway pressure (CPAP) therapy adherence among obstructive sleep apnea (OSA) patients, as well as simulations on a broader class of synthetic transition matrices.

Fair Clustering Under a Bounded Cost

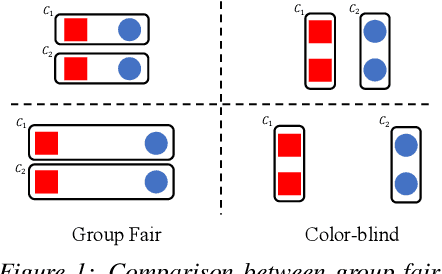
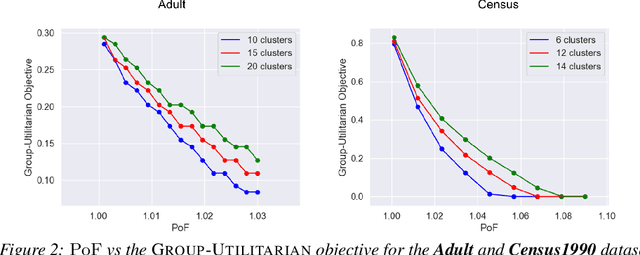
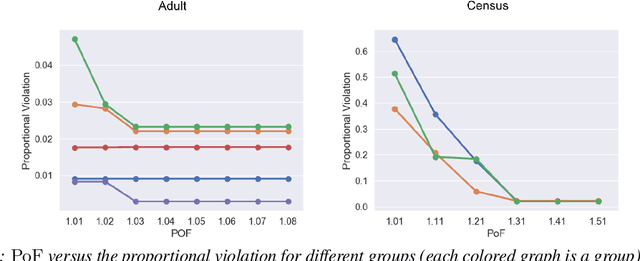
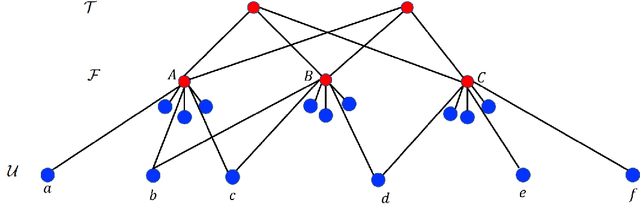
Clustering is a fundamental unsupervised learning problem where a dataset is partitioned into clusters that consist of nearby points in a metric space. A recent variant, fair clustering, associates a color with each point representing its group membership and requires that each color has (approximately) equal representation in each cluster to satisfy group fairness. In this model, the cost of the clustering objective increases due to enforcing fairness in the algorithm. The relative increase in the cost, the ''price of fairness,'' can indeed be unbounded. Therefore, in this paper we propose to treat an upper bound on the clustering objective as a constraint on the clustering problem, and to maximize equality of representation subject to it. We consider two fairness objectives: the group utilitarian objective and the group egalitarian objective, as well as the group leximin objective which generalizes the group egalitarian objective. We derive fundamental lower bounds on the approximation of the utilitarian and egalitarian objectives and introduce algorithms with provable guarantees for them. For the leximin objective we introduce an effective heuristic algorithm. We further derive impossibility results for other natural fairness objectives. We conclude with experimental results on real-world datasets that demonstrate the validity of our algorithms.

Fair Disaster Containment via Graph-Cut Problems

Graph cut problems form a fundamental problem type in combinatorial optimization, and are a central object of study in both theory and practice. In addition, the study of fairness in Algorithmic Design and Machine Learning has recently received significant attention, with many different notions proposed and analyzed in a variety of contexts. In this paper we initiate the study of fairness for graph cut problems by giving the first fair definitions for them, and subsequently we demonstrate appropriate algorithmic techniques that yield a rigorous theoretical analysis. Specifically, we incorporate two different definitions of fairness, namely demographic and probabilistic individual fairness, in a particular cut problem modeling disaster containment scenarios. Our results include a variety of approximation algorithms with provable theoretical guarantees.

A New Notion of Individually Fair Clustering: $α$-Equitable $k$-Center

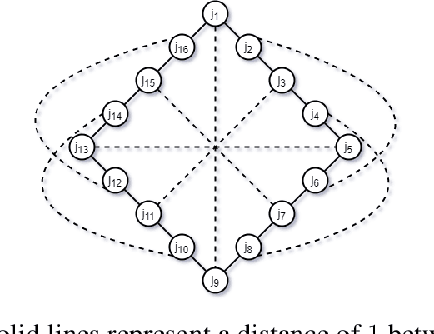
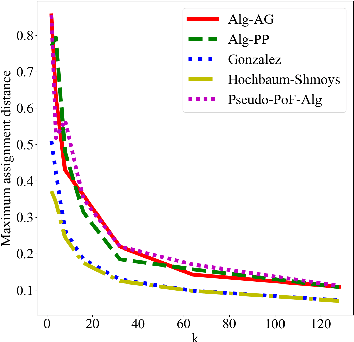
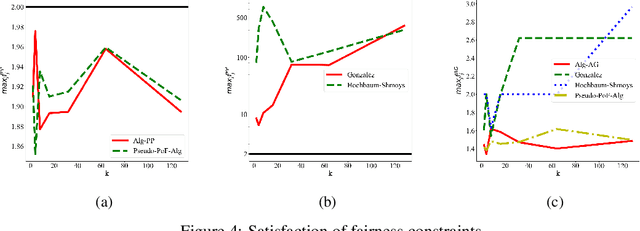
Clustering is a fundamental problem in unsupervised machine learning, and fair variants of it have recently received significant attention. In this work we introduce a novel definition of fairness for clustering problems. Specifically, in our model each point $j$ has a set of other points $\mathcal{S}_j$ that it perceives as similar to itself, and it feels that it is fairly treated, if the quality of service it receives in the solution is $\alpha$-close to that of the points in $\mathcal{S}_j$. We begin our study by answering questions regarding the structure of the problem, namely for what values of $\alpha$ the problem is well-defined, and what the behavior of the Price of Fairness (PoF) for it is. For the well-defined region of $\alpha$, we provide efficient and easily implementable approximation algorithms for the $k$-center objective, which in certain cases also enjoy bounded PoF guarantees. We finally complement our analysis by an extensive suite of experiments that validates the effectiveness of our theoretical results.

Fairness, Semi-Supervised Learning, and More: A General Framework for Clustering with Stochastic Pairwise Constraints

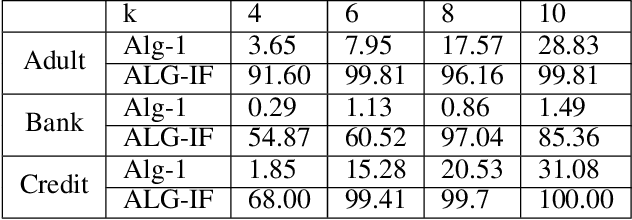
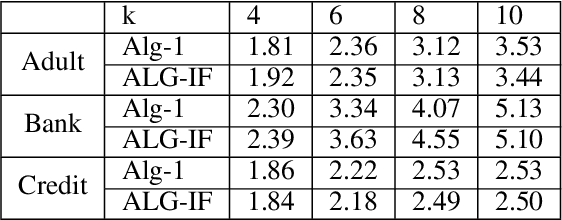
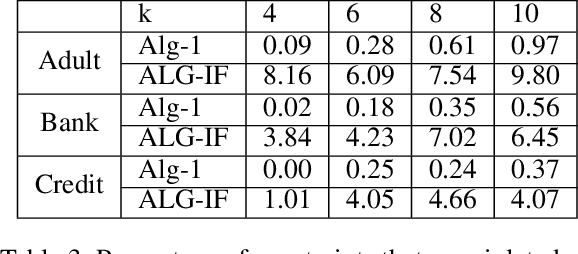
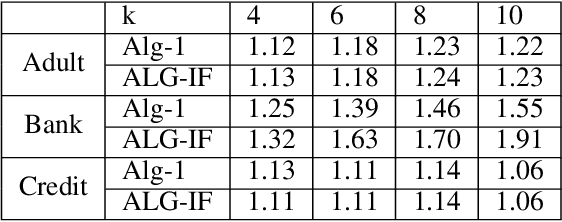
Metric clustering is fundamental in areas ranging from Combinatorial Optimization and Data Mining, to Machine Learning and Operations Research. However, in a variety of situations we may have additional requirements or knowledge, distinct from the underlying metric, regarding which pairs of points should be clustered together. To capture and analyze such scenarios, we introduce a novel family of \emph{stochastic pairwise constraints}, which we incorporate into several essential clustering objectives (radius/median/means). Moreover, we demonstrate that these constraints can succinctly model an intriguing collection of applications, including among others \emph{Individual Fairness} in clustering and \emph{Must-link} constraints in semi-supervised learning. Our main result consists of a general framework that yields approximation algorithms with provable guarantees for important clustering objectives, while at the same time producing solutions that respect the stochastic pairwise constraints. Furthermore, for certain objectives we devise improved results in the case of Must-link constraints, which are also the best possible from a theoretical perspective. Finally, we present experimental evidence that validates the effectiveness of our algorithms.

A Pairwise Fair and Community-preserving Approach to k-Center Clustering

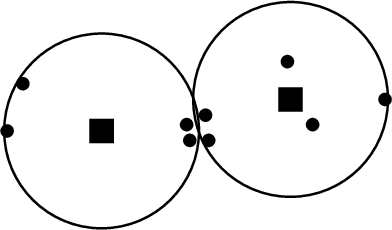
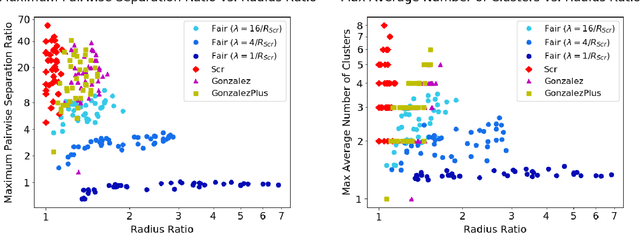
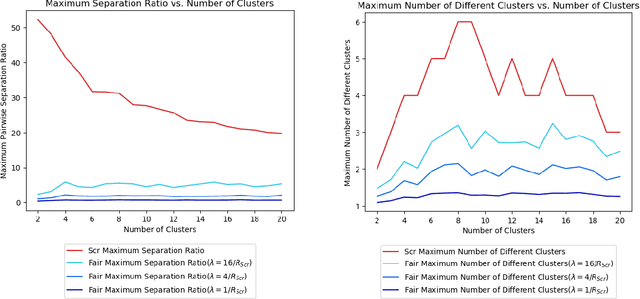
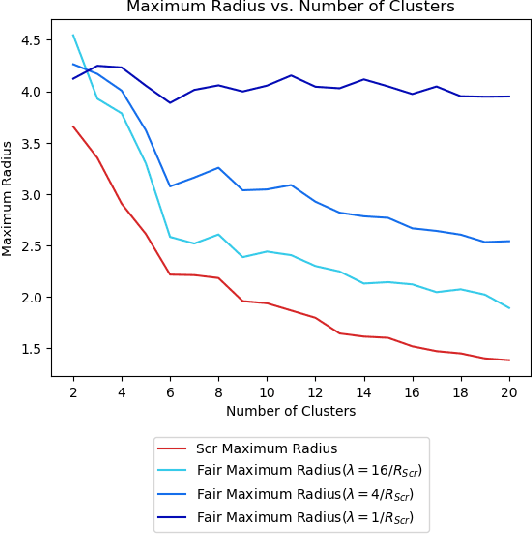
Clustering is a foundational problem in machine learning with numerous applications. As machine learning increases in ubiquity as a backend for automated systems, concerns about fairness arise. Much of the current literature on fairness deals with discrimination against protected classes in supervised learning (group fairness). We define a different notion of fair clustering wherein the probability that two points (or a community of points) become separated is bounded by an increasing function of their pairwise distance (or community diameter). We capture the situation where data points represent people who gain some benefit from being clustered together. Unfairness arises when certain points are deterministically separated, either arbitrarily or by someone who intends to harm them as in the case of gerrymandering election districts. In response, we formally define two new types of fairness in the clustering setting, pairwise fairness and community preservation. To explore the practicality of our fairness goals, we devise an approach for extending existing $k$-center algorithms to satisfy these fairness constraints. Analysis of this approach proves that reasonable approximations can be achieved while maintaining fairness. In experiments, we compare the effectiveness of our approach to classical $k$-center algorithms/heuristics and explore the tradeoff between optimal clustering and fairness.

Balancing the Tradeoff between Profit and Fairness in Rideshare Platforms During High-Demand Hours

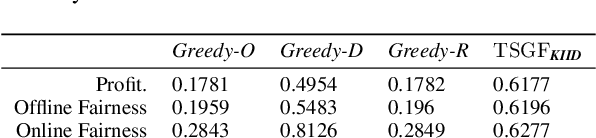
Rideshare platforms, when assigning requests to drivers, tend to maximize profit for the system and/or minimize waiting time for riders. Such platforms can exacerbate biases that drivers may have over certain types of requests. We consider the case of peak hours when the demand for rides is more than the supply of drivers. Drivers are well aware of their advantage during the peak hours and can choose to be selective about which rides to accept. Moreover, if in such a scenario, the assignment of requests to drivers (by the platform) is made only to maximize profit and/or minimize wait time for riders, requests of a certain type (e.g. from a non-popular pickup location, or to a non-popular drop-off location) might never be assigned to a driver. Such a system can be highly unfair to riders. However, increasing fairness might come at a cost of the overall profit made by the rideshare platform. To balance these conflicting goals, we present a flexible, non-adaptive algorithm, \lpalg, that allows the platform designer to control the profit and fairness of the system via parameters $\alpha$ and $\beta$ respectively. We model the matching problem as an online bipartite matching where the set of drivers is offline and requests arrive online. Upon the arrival of a request, we use \lpalg to assign it to a driver (the driver might then choose to accept or reject it) or reject the request. We formalize the measures of profit and fairness in our setting and show that by using \lpalg, the competitive ratios for profit and fairness measures would be no worse than $\alpha/e$ and $\beta/e$ respectively. Extensive experimental results on both real-world and synthetic datasets confirm the validity of our theoretical lower bounds. Additionally, they show that $\lpalg$ under some choice of $(\alpha, \beta)$ can beat two natural heuristics, Greedy and Uniform, on \emph{both} fairness and profit.