Individual Preference Stability for Clustering

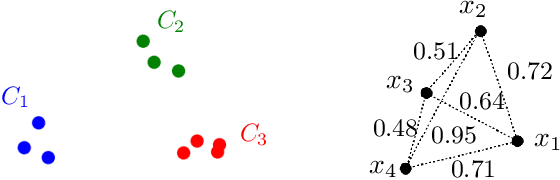
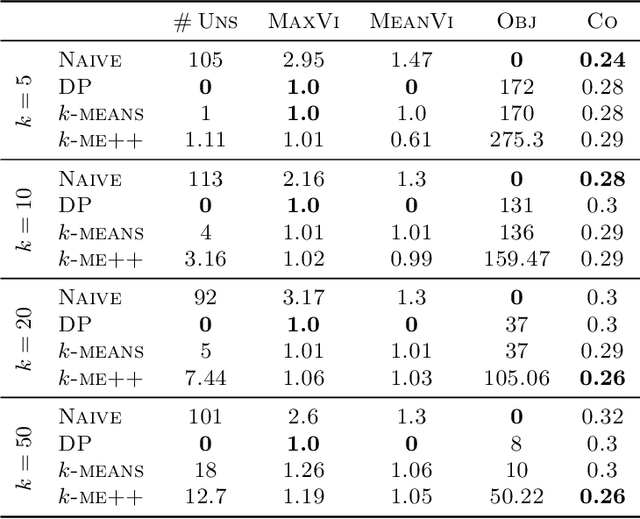
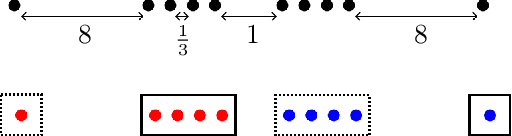
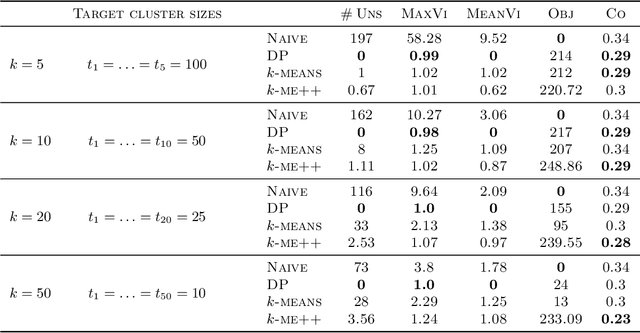
In this paper, we propose a natural notion of individual preference (IP) stability for clustering, which asks that every data point, on average, is closer to the points in its own cluster than to the points in any other cluster. Our notion can be motivated from several perspectives, including game theory and algorithmic fairness. We study several questions related to our proposed notion. We first show that deciding whether a given data set allows for an IP-stable clustering in general is NP-hard. As a result, we explore the design of efficient algorithms for finding IP-stable clusterings in some restricted metric spaces. We present a polytime algorithm to find a clustering satisfying exact IP-stability on the real line, and an efficient algorithm to find an IP-stable 2-clustering for a tree metric. We also consider relaxing the stability constraint, i.e., every data point should not be too far from its own cluster compared to any other cluster. For this case, we provide polytime algorithms with different guarantees. We evaluate some of our algorithms and several standard clustering approaches on real data sets.

A Pairwise Fair and Community-preserving Approach to k-Center Clustering

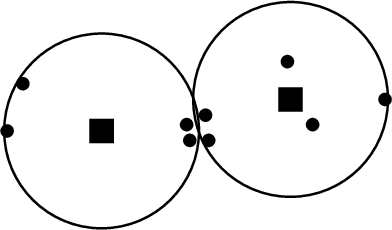
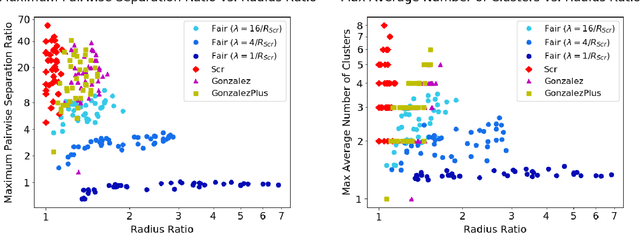
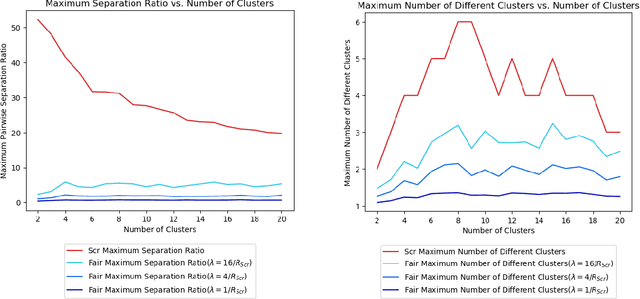
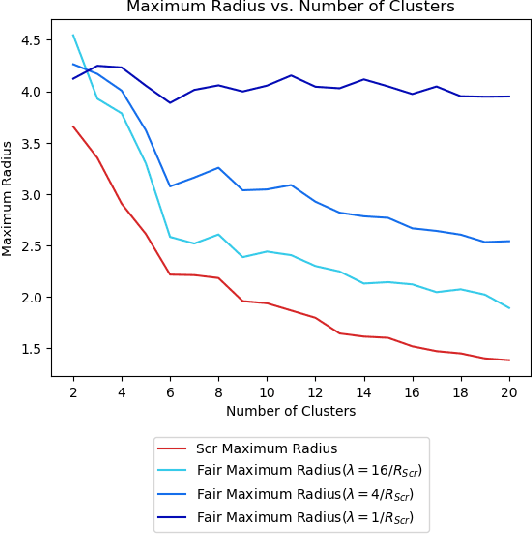
Clustering is a foundational problem in machine learning with numerous applications. As machine learning increases in ubiquity as a backend for automated systems, concerns about fairness arise. Much of the current literature on fairness deals with discrimination against protected classes in supervised learning (group fairness). We define a different notion of fair clustering wherein the probability that two points (or a community of points) become separated is bounded by an increasing function of their pairwise distance (or community diameter). We capture the situation where data points represent people who gain some benefit from being clustered together. Unfairness arises when certain points are deterministically separated, either arbitrarily or by someone who intends to harm them as in the case of gerrymandering election districts. In response, we formally define two new types of fairness in the clustering setting, pairwise fairness and community preservation. To explore the practicality of our fairness goals, we devise an approach for extending existing $k$-center algorithms to satisfy these fairness constraints. Analysis of this approach proves that reasonable approximations can be achieved while maintaining fairness. In experiments, we compare the effectiveness of our approach to classical $k$-center algorithms/heuristics and explore the tradeoff between optimal clustering and fairness.

Algorithms for Optimal Diverse Matching

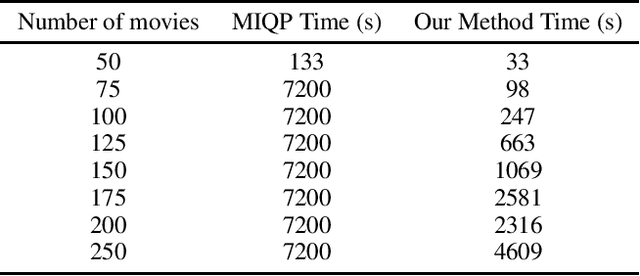
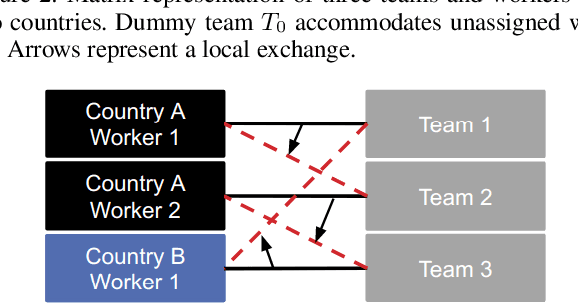
Bipartite b-matching, where agents on one side of a market are matched to one or more agents or items on the other, is a classical model that is used in myriad application areas such as healthcare, advertising, education, and general resource allocation. Traditionally, the primary goal of such models is to maximize a linear function of the constituent matches (e.g., linear social welfare maximization) subject to some constraints. Recent work has studied a new goal of balancing whole-match diversity and economic efficiency, where the objective is instead a monotone submodular function over the matching. These more general models are largely NP-hard. In this work, we develop a combinatorial algorithm that constructs provably-optimal diverse b-matchings in pseudo-polynomial time. Then, we show how to extend our algorithm to solve new variations of the diverse b-matching problem. We then compare directly, on real-world datasets, against the state-of-the-art, quadratic-programming-based approach to solving diverse b-matching problems and show that our method outperforms it in both speed and (anytime) solution quality.

Minimizing Uncertainty through Sensor Placement with Angle Constraints

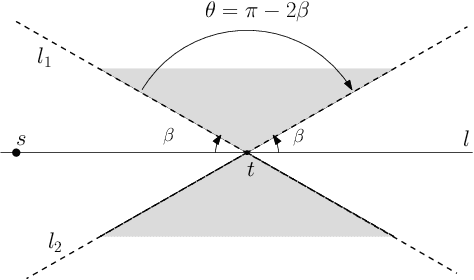
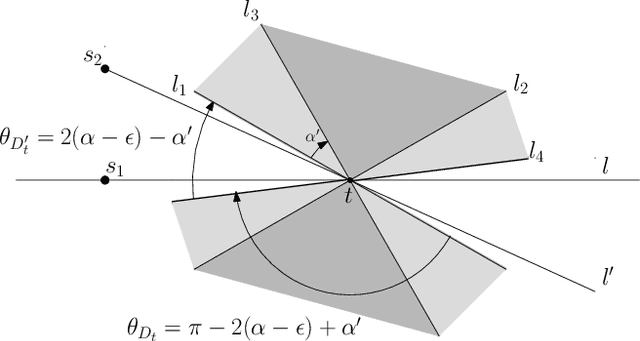
We study the problem of sensor placement in environments in which localization is a necessity, such as ad-hoc wireless sensor networks that allow the placement of a few anchors that know their location or sensor arrays that are tracking a target. In most of these situations, the quality of localization depends on the relative angle between the target and the pair of sensors observing it. In this paper, we consider placing a small number of sensors which ensure good angular $\alpha$-coverage: given $\alpha$ in $[0,\pi/2]$, for each target location $t$, there must be at least two sensors $s_1$ and $s_2$ such that the $\angle(s_1 t s_2)$ is in the interval $[\alpha, \pi-\alpha]$. One of the main difficulties encountered in such problems is that since the constraints depend on at least two sensors, building a solution must account for the inherent dependency between selected sensors, a feature that generic Set Cover techniques do not account for. We introduce a general framework that guarantees an angular coverage that is arbitrarily close to $\alpha$ for any $\alpha <= \pi/3$ and apply it to a variety of problems to get bi-criteria approximations. When the angular coverage is required to be at least a constant fraction of $\alpha$, we obtain results that are strictly better than what standard geometric Set Cover methods give. When the angular coverage is required to be at least $(1-1/\delta)\cdot\alpha$, we obtain a $\mathcal{O}(\log \delta)$- approximation for sensor placement with $\alpha$-coverage on the plane. In the presence of additional distance or visibility constraints, the framework gives a $\mathcal{O}(\log\delta\cdot\log k_{OPT})$-approximation, where $k_{OPT}$ is the size of the optimal solution. We also use our framework to give a $\mathcal{O}(\log \delta)$-approximation that ensures $(1-1/\delta)\cdot \alpha$-coverage and covers every target within distance $3R$.

On Correcting Inputs: Inverse Optimization for Online Structured Prediction

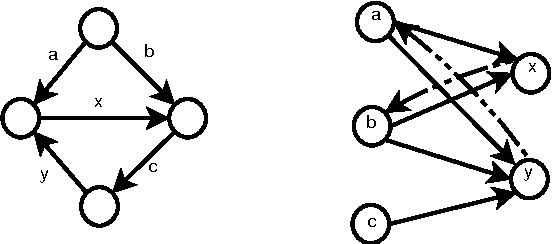
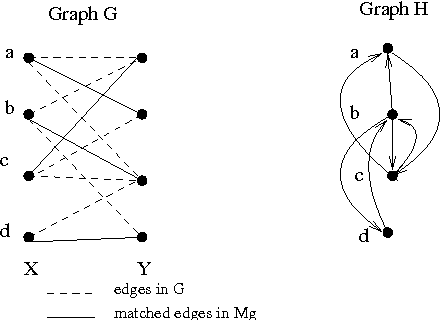
Algorithm designers typically assume that the input data is correct, and then proceed to find "optimal" or "sub-optimal" solutions using this input data. However this assumption of correct data does not always hold in practice, especially in the context of online learning systems where the objective is to learn appropriate feature weights given some training samples. Such scenarios necessitate the study of inverse optimization problems where one is given an input instance as well as a desired output and the task is to adjust the input data so that the given output is indeed optimal. Motivated by learning structured prediction models, in this paper we consider inverse optimization with a margin, i.e., we require the given output to be better than all other feasible outputs by a desired margin. We consider such inverse optimization problems for maximum weight matroid basis, matroid intersection, perfect matchings, minimum cost maximum flows, and shortest paths and derive the first known results for such problems with a non-zero margin. The effectiveness of these algorithmic approaches to online learning for structured prediction is also discussed.