Fair Labeled Clustering

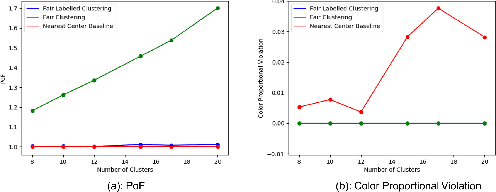
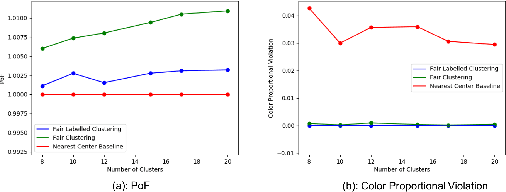
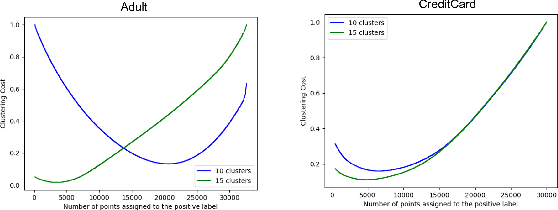
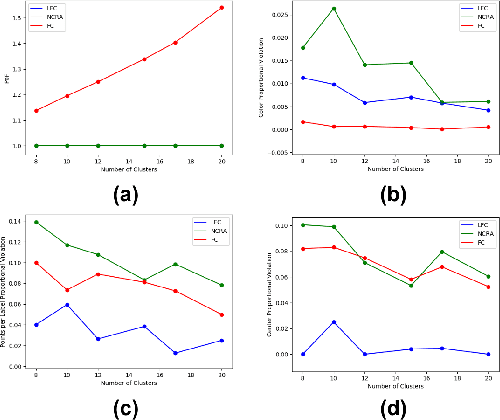
Numerous algorithms have been produced for the fundamental problem of clustering under many different notions of fairness. Perhaps the most common family of notions currently studied is group fairness, in which proportional group representation is ensured in every cluster. We extend this direction by considering the downstream application of clustering and how group fairness should be ensured for such a setting. Specifically, we consider a common setting in which a decision-maker runs a clustering algorithm, inspects the center of each cluster, and decides an appropriate outcome (label) for its corresponding cluster. In hiring for example, there could be two outcomes, positive (hire) or negative (reject), and each cluster would be assigned one of these two outcomes. To ensure group fairness in such a setting, we would desire proportional group representation in every label but not necessarily in every cluster as is done in group fair clustering. We provide algorithms for such problems and show that in contrast to their NP-hard counterparts in group fair clustering, they permit efficient solutions. We also consider a well-motivated alternative setting where the decision-maker is free to assign labels to the clusters regardless of the centers' positions in the metric space. We show that this setting exhibits interesting transitions from computationally hard to easy according to additional constraints on the problem. Moreover, when the constraint parameters take on natural values we show a randomized algorithm for this setting that always achieves an optimal clustering and satisfies the fairness constraints in expectation. Finally, we run experiments on real world datasets that validate the effectiveness of our algorithms.

Centralized Fairness for Redistricting

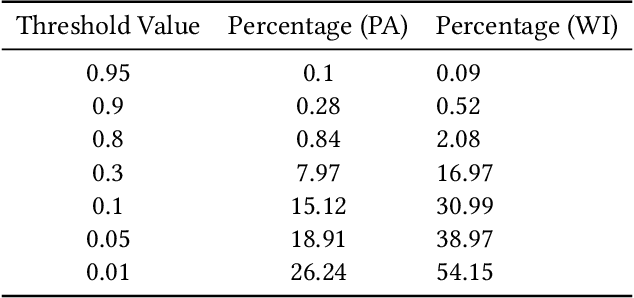
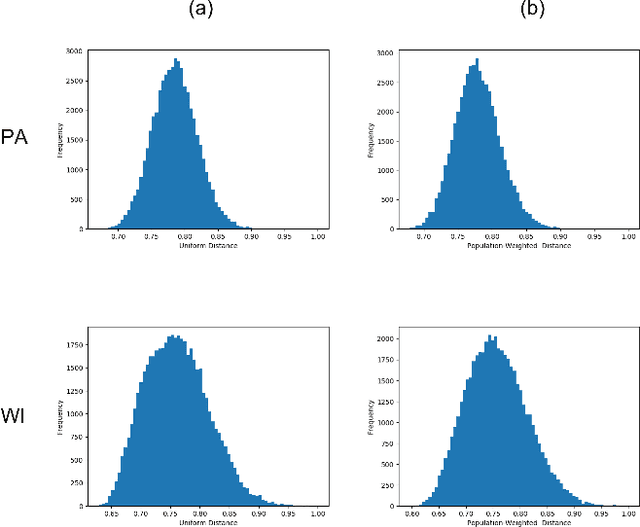
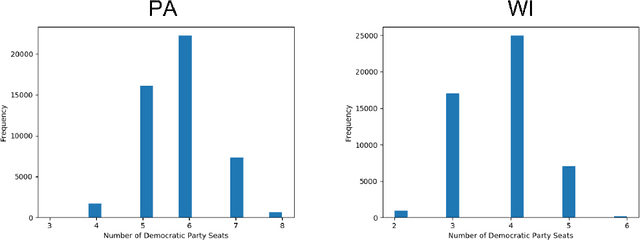
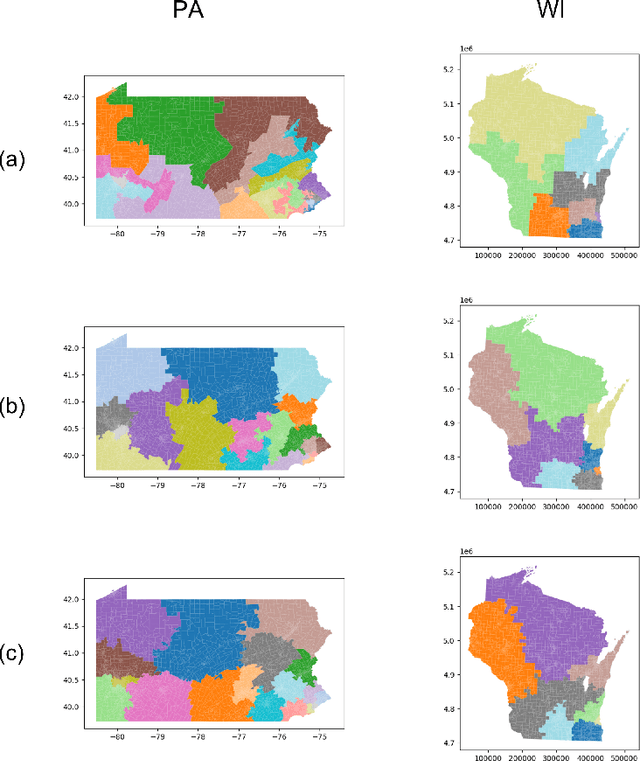
In representative democracy, the electorate is often partitioned into districts with each district electing a representative. However, these systems have proven vulnerable to the practice of partisan gerrymandering which involves drawing districts that elect more representatives from a given political party. Additionally, computer-based methods have dramatically enhanced the ability to draw districts that drastically favor one party over others. On the positive side, researchers have recently developed tools for measuring how gerrymandered a redistricting map is by comparing it to a large set of randomly-generated district maps. While these efforts to test whether a district map is "gerrymandered" have achieved real-world impact, the question of how best to draw districts remains very open. Many attempts to automate the redistricting process have been proposed, but not adopted into practice. Typically, they have focused on optimizing certain properties (e.g., geographical compactness or partisan competitiveness of districts) and argued that the properties are desirable. In this work, we take an alternative approach which seeks to find the most "typical" redistricting map. More precisely, we introduce a family of well-motivated distance measures over redistricting maps. Then, by generating a large collection of maps using sampling techniques, we select the map which minimizes the sum of the distances from the collection, i.e., the most "central" map. We produce scalable, linear-time algorithms and derive sample complexity guarantees. Empirically, we show the validity of our algorithms over real world redistricting problems.

Fair Clustering Under a Bounded Cost

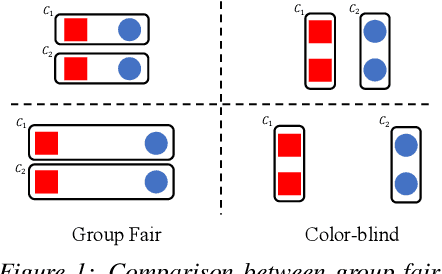
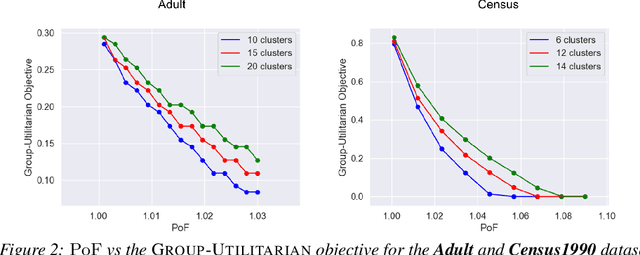
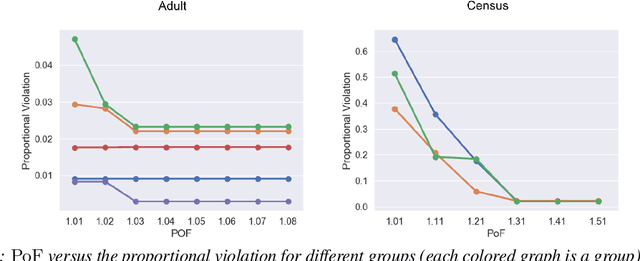
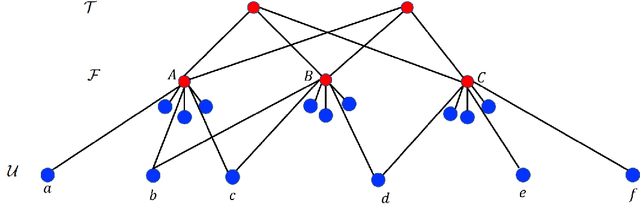
Clustering is a fundamental unsupervised learning problem where a dataset is partitioned into clusters that consist of nearby points in a metric space. A recent variant, fair clustering, associates a color with each point representing its group membership and requires that each color has (approximately) equal representation in each cluster to satisfy group fairness. In this model, the cost of the clustering objective increases due to enforcing fairness in the algorithm. The relative increase in the cost, the ''price of fairness,'' can indeed be unbounded. Therefore, in this paper we propose to treat an upper bound on the clustering objective as a constraint on the clustering problem, and to maximize equality of representation subject to it. We consider two fairness objectives: the group utilitarian objective and the group egalitarian objective, as well as the group leximin objective which generalizes the group egalitarian objective. We derive fundamental lower bounds on the approximation of the utilitarian and egalitarian objectives and introduce algorithms with provable guarantees for them. For the leximin objective we introduce an effective heuristic algorithm. We further derive impossibility results for other natural fairness objectives. We conclude with experimental results on real-world datasets that demonstrate the validity of our algorithms.

Fairness, Semi-Supervised Learning, and More: A General Framework for Clustering with Stochastic Pairwise Constraints

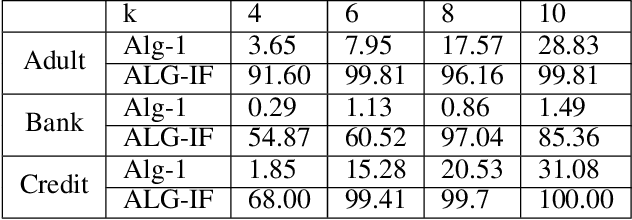
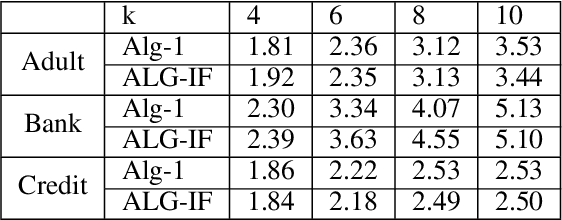
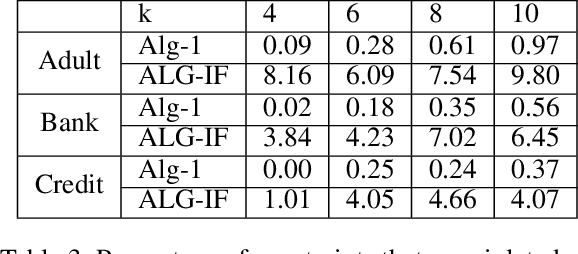
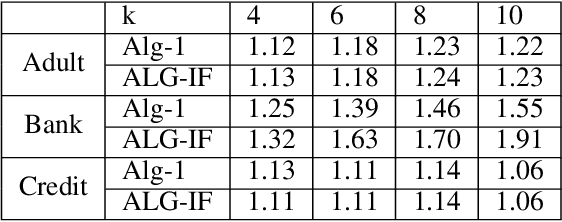
Metric clustering is fundamental in areas ranging from Combinatorial Optimization and Data Mining, to Machine Learning and Operations Research. However, in a variety of situations we may have additional requirements or knowledge, distinct from the underlying metric, regarding which pairs of points should be clustered together. To capture and analyze such scenarios, we introduce a novel family of \emph{stochastic pairwise constraints}, which we incorporate into several essential clustering objectives (radius/median/means). Moreover, we demonstrate that these constraints can succinctly model an intriguing collection of applications, including among others \emph{Individual Fairness} in clustering and \emph{Must-link} constraints in semi-supervised learning. Our main result consists of a general framework that yields approximation algorithms with provable guarantees for important clustering objectives, while at the same time producing solutions that respect the stochastic pairwise constraints. Furthermore, for certain objectives we devise improved results in the case of Must-link constraints, which are also the best possible from a theoretical perspective. Finally, we present experimental evidence that validates the effectiveness of our algorithms.

A Pairwise Fair and Community-preserving Approach to k-Center Clustering

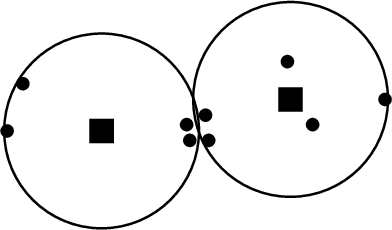
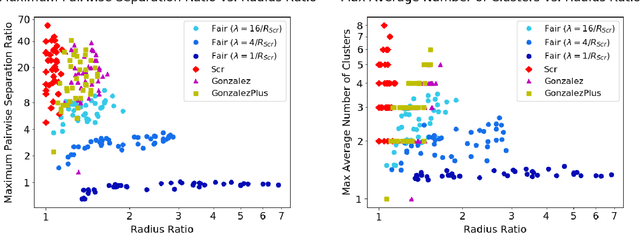
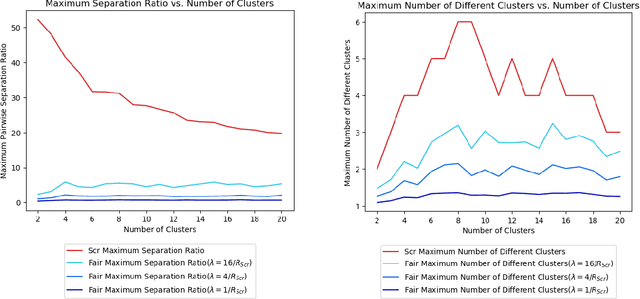
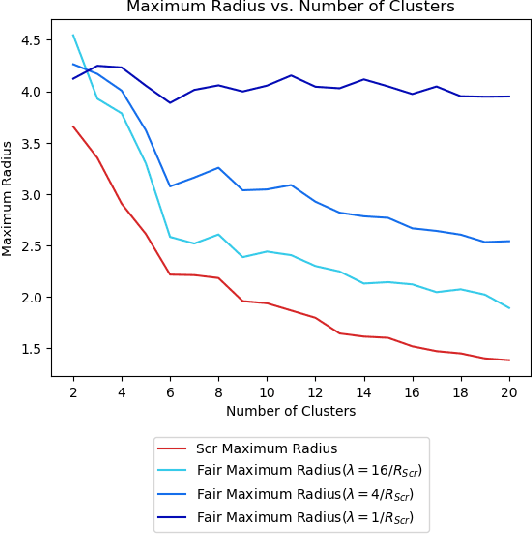
Clustering is a foundational problem in machine learning with numerous applications. As machine learning increases in ubiquity as a backend for automated systems, concerns about fairness arise. Much of the current literature on fairness deals with discrimination against protected classes in supervised learning (group fairness). We define a different notion of fair clustering wherein the probability that two points (or a community of points) become separated is bounded by an increasing function of their pairwise distance (or community diameter). We capture the situation where data points represent people who gain some benefit from being clustered together. Unfairness arises when certain points are deterministically separated, either arbitrarily or by someone who intends to harm them as in the case of gerrymandering election districts. In response, we formally define two new types of fairness in the clustering setting, pairwise fairness and community preservation. To explore the practicality of our fairness goals, we devise an approach for extending existing $k$-center algorithms to satisfy these fairness constraints. Analysis of this approach proves that reasonable approximations can be achieved while maintaining fairness. In experiments, we compare the effectiveness of our approach to classical $k$-center algorithms/heuristics and explore the tradeoff between optimal clustering and fairness.

Probabilistic Fair Clustering

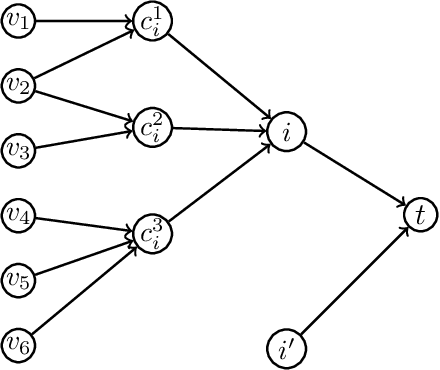
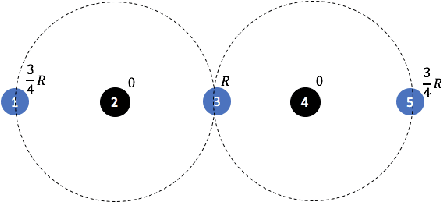
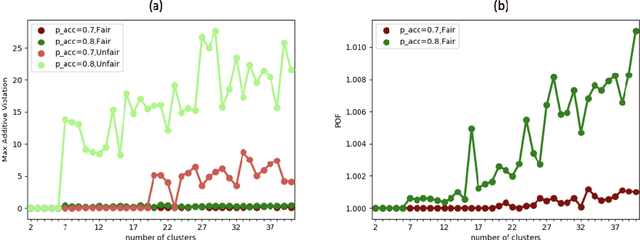
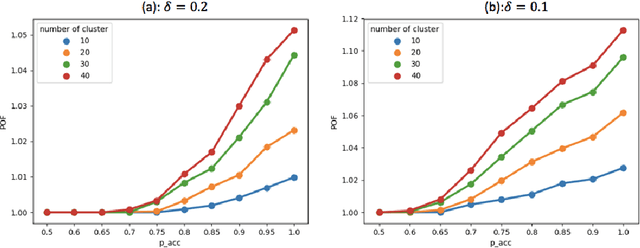
In clustering problems, a central decision-maker is given a complete metric graph over vertices and must provide a clustering of vertices that minimizes some objective function. In fair clustering problems, vertices are endowed with a color (e.g., membership in a group), and the features of a valid clustering might also include the representation of colors in that clustering. Prior work in fair clustering assumes complete knowledge of group membership. In this paper, we generalize prior work by assuming imperfect knowledge of group membership through probabilistic assignments. We present clustering algorithms in this more general setting with approximation ratio guarantees. We also address the problem of "metric membership", where different groups have a notion of order and distance. Experiments are conducted using our proposed algorithms as well as baselines to validate our approach and also surface nuanced concerns when group membership is not known deterministically.

Attenuate Locally, Win Globally: An Attenuation-based Framework for Online Stochastic Matching with Timeouts

Online matching problems have garnered significant attention in recent years due to numerous applications in e-commerce, online advertisements, ride-sharing, etc. Many of them capture the uncertainty in the real world by including stochasticity in both the arrival process and the matching process. The Online Stochastic Matching with Timeouts problem introduced by Bansal, et al., (Algorithmica, 2012) models matching markets (e.g., E-Bay, Amazon). Buyers arrive from an independent and identically distributed (i.i.d.) known distribution on buyer profiles and can be shown a list of items one at a time. Each buyer has some probability of purchasing each item and a limit (timeout) on the number of items they can be shown. Bansal et al., (Algorithmica, 2012) gave a 0.12-competitive algorithm which was improved by Adamczyk, et al., (ESA, 2015) to 0.24. We present an online attenuation framework that uses an algorithm for offline stochastic matching as a black box. On the upper bound side, we show that this framework, combined with a black-box adapted from Bansal et al., (Algorithmica, 2012), yields an online algorithm which nearly doubles the ratio to 0.46. On the lower bound side, we show that no algorithm can achieve a ratio better than 0.632 using the standard LP for this problem. This framework has a high potential for further improvements since new algorithms for offline stochastic matching can directly improve the ratio for the online problem. Our online framework also has the potential for a variety of extensions. For example, we introduce a natural generalization: Online Stochastic Matching with Two-sided Timeouts in which both online and offline vertices have timeouts. Our framework provides the first algorithm for this problem achieving a ratio of 0.30. We once again use the algorithm of Adamczyk et al., (ESA, 2015) as a black-box and plug-it into our framework.