Seyed A. Esmaeili
Welfare-Centric Clustering
Aug 14, 2025Abstract:Fair clustering has traditionally focused on ensuring equitable group representation or equalizing group-specific clustering costs. However, Dickerson et al. (2025) recently showed that these fairness notions may yield undesirable or unintuitive clustering outcomes and advocated for a welfare-centric clustering approach that models the utilities of the groups. In this work, we model group utilities based on both distances and proportional representation and formalize two optimization objectives based on welfare-centric clustering: the Rawlsian (Egalitarian) objective and the Utilitarian objective. We introduce novel algorithms for both objectives and prove theoretical guarantees for them. Empirical evaluations on multiple real-world datasets demonstrate that our methods significantly outperform existing fair clustering baselines.
Fair Clustering: Critique, Caveats, and Future Directions
Jun 22, 2024Abstract:Clustering is a fundamental problem in machine learning and operations research. Therefore, given the fact that fairness considerations have become of paramount importance in algorithm design, fairness in clustering has received significant attention from the research community. The literature on fair clustering has resulted in a collection of interesting fairness notions and elaborate algorithms. In this paper, we take a critical view of fair clustering, identifying a collection of ignored issues such as the lack of a clear utility characterization and the difficulty in accounting for the downstream effects of a fair clustering algorithm in machine learning settings. In some cases, we demonstrate examples where the application of a fair clustering algorithm can have significant negative impacts on social welfare. We end by identifying a collection of steps that would lead towards more impactful research in fair clustering.
How to Strategize Human Content Creation in the Era of GenAI?
Jun 07, 2024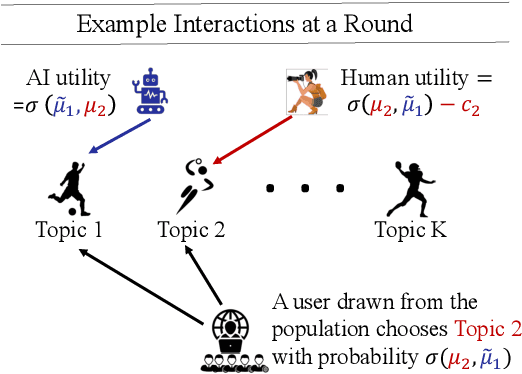
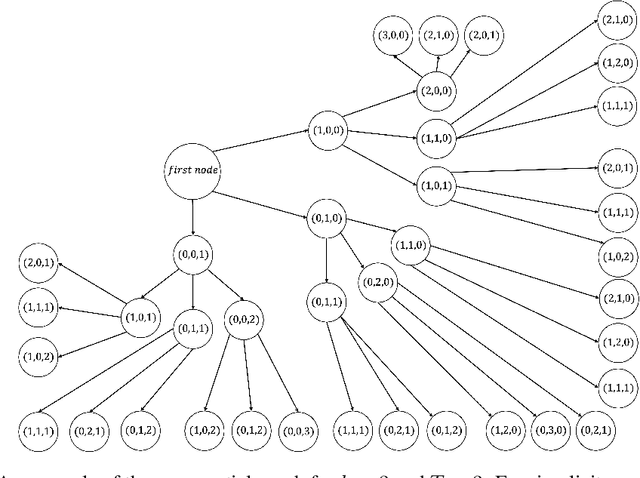
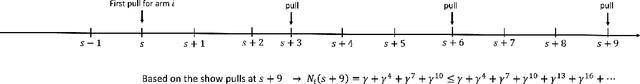
Abstract:Generative AI (GenAI) will have significant impact on content creation platforms. In this paper, we study the dynamic competition between a GenAI and a human contributor. Unlike the human, the GenAI's content only improves when more contents are created by human over the time; however, GenAI has the advantage of generating content at a lower cost. We study the algorithmic problem in this dynamic competition model about how the human contributor can maximize her utility when competing against the GenAI for content generation over a set of topics. In time-sensitive content domains (e.g., news or pop music creation) where contents' value diminishes over time, we show that there is no polynomial time algorithm for finding the human's optimal (dynamic) strategy, unless the randomized exponential time hypothesis is false. Fortunately, we are able to design a polynomial time algorithm that naturally cycles between myopically optimizing over a short time window and pausing and provably guarantees an approximation ratio of $\frac{1}{2}$. We then turn to time-insensitive content domains where contents do not lose their value (e.g., contents on history facts). Interestingly, we show that this setting permits a polynomial time algorithm that maximizes the human's utility in the long run.
Robust Fair Clustering with Group Membership Uncertainty Sets
Jun 02, 2024Abstract:We study the canonical fair clustering problem where each cluster is constrained to have close to population-level representation of each group. Despite significant attention, the salient issue of having incomplete knowledge about the group membership of each point has been superficially addressed. In this paper, we consider a setting where errors exist in the assigned group memberships. We introduce a simple and interpretable family of error models that require a small number of parameters to be given by the decision maker. We then present an algorithm for fair clustering with provable robustness guarantees. Our framework enables the decision maker to trade off between the robustness and the clustering quality. Unlike previous work, our algorithms are backed by worst-case theoretical guarantees. Finally, we empirically verify the performance of our algorithm on real world datasets and show its superior performance over existing baselines.
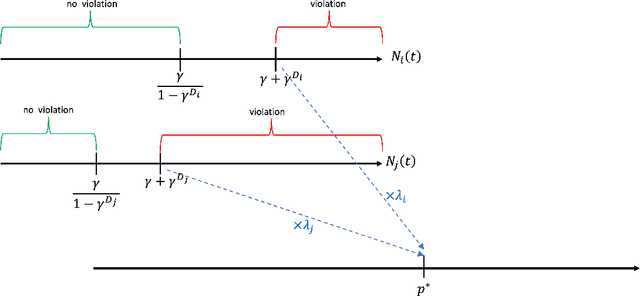
Robust and Performance Incentivizing Algorithms for Multi-Armed Bandits with Strategic Agents
Dec 13, 2023
Abstract:We consider a variant of the stochastic multi-armed bandit problem. Specifically, the arms are strategic agents who can improve their rewards or absorb them. The utility of an agent increases if she is pulled more or absorbs more of her rewards but decreases if she spends more effort improving her rewards. Agents have heterogeneous properties, specifically having different means and able to improve their rewards up to different levels. Further, a non-empty subset of agents are ''honest'' and in the worst case always give their rewards without absorbing any part. The principal wishes to obtain a high revenue (cumulative reward) by designing a mechanism that incentives top level performance at equilibrium. At the same time, the principal wishes to be robust and obtain revenue at least at the level of the honest agent with the highest mean in case of non-equilibrium behaviour. We identify a class of MAB algorithms which we call performance incentivizing which satisfy a collection of properties and show that they lead to mechanisms that incentivize top level performance at equilibrium and are robust under any strategy profile. Interestingly, we show that UCB is an example of such a MAB algorithm. Further, in the case where the top performance level is unknown we show that combining second price auction ideas with performance incentivizing algorithms achieves performance at least at the second top level while also being robust.
Doubly Constrained Fair Clustering
May 31, 2023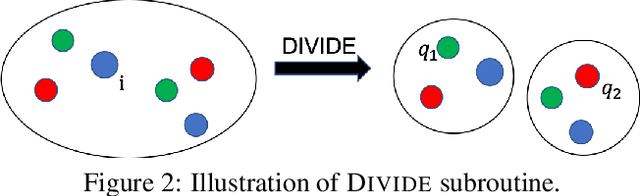
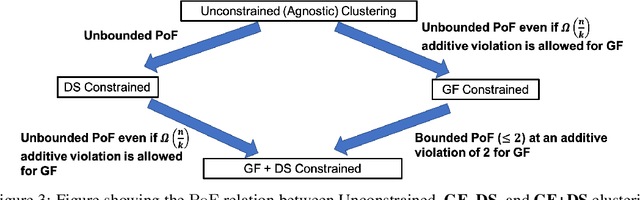
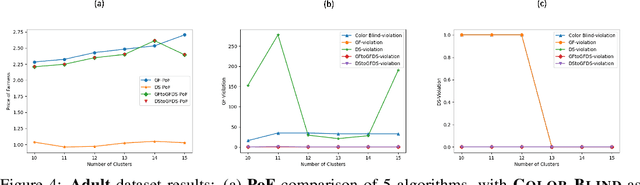
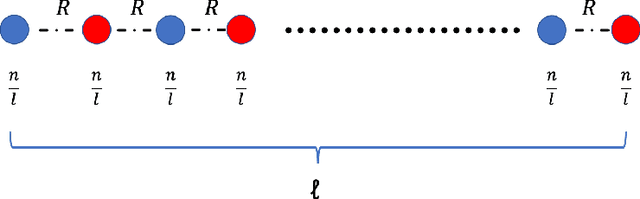
Abstract:The remarkable attention which fair clustering has received in the last few years has resulted in a significant number of different notions of fairness. Despite the fact that these notions are well-justified, they are often motivated and studied in a disjoint manner where one fairness desideratum is considered exclusively in isolation from the others. This leaves the understanding of the relations between different fairness notions as an important open problem in fair clustering. In this paper, we take the first step in this direction. Specifically, we consider the two most prominent demographic representation fairness notions in clustering: (1) Group Fairness (GF), where the different demographic groups are supposed to have close to population-level representation in each cluster and (2) Diversity in Center Selection (DS), where the selected centers are supposed to have close to population-level representation of each group. We show that given a constant approximation algorithm for one constraint (GF or DS only) we can obtain a constant approximation solution that satisfies both constraints simultaneously. Interestingly, we prove that any given solution that satisfies the GF constraint can always be post-processed at a bounded degradation to the clustering cost to additionally satisfy the DS constraint while the reverse is not true. Furthermore, we show that both GF and DS are incompatible (having an empty feasibility set in the worst case) with a collection of other distance-based fairness notions. Finally, we carry experiments to validate our theoretical findings.
Fair Labeled Clustering
May 28, 2022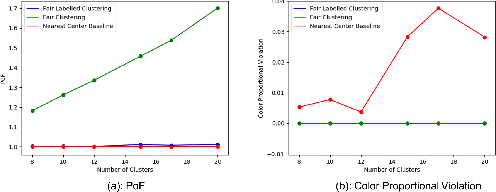
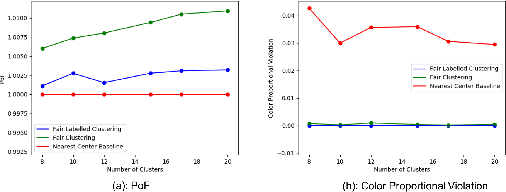
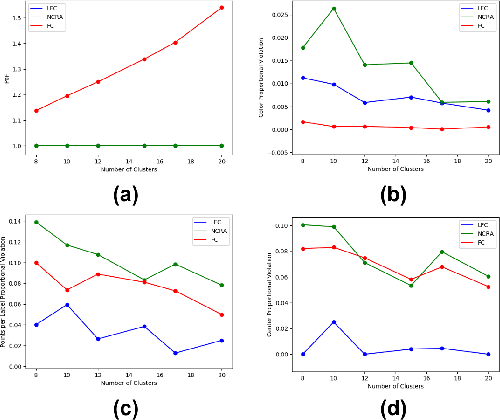
Abstract:Numerous algorithms have been produced for the fundamental problem of clustering under many different notions of fairness. Perhaps the most common family of notions currently studied is group fairness, in which proportional group representation is ensured in every cluster. We extend this direction by considering the downstream application of clustering and how group fairness should be ensured for such a setting. Specifically, we consider a common setting in which a decision-maker runs a clustering algorithm, inspects the center of each cluster, and decides an appropriate outcome (label) for its corresponding cluster. In hiring for example, there could be two outcomes, positive (hire) or negative (reject), and each cluster would be assigned one of these two outcomes. To ensure group fairness in such a setting, we would desire proportional group representation in every label but not necessarily in every cluster as is done in group fair clustering. We provide algorithms for such problems and show that in contrast to their NP-hard counterparts in group fair clustering, they permit efficient solutions. We also consider a well-motivated alternative setting where the decision-maker is free to assign labels to the clusters regardless of the centers' positions in the metric space. We show that this setting exhibits interesting transitions from computationally hard to easy according to additional constraints on the problem. Moreover, when the constraint parameters take on natural values we show a randomized algorithm for this setting that always achieves an optimal clustering and satisfies the fairness constraints in expectation. Finally, we run experiments on real world datasets that validate the effectiveness of our algorithms.
Centralized Fairness for Redistricting
Mar 02, 2022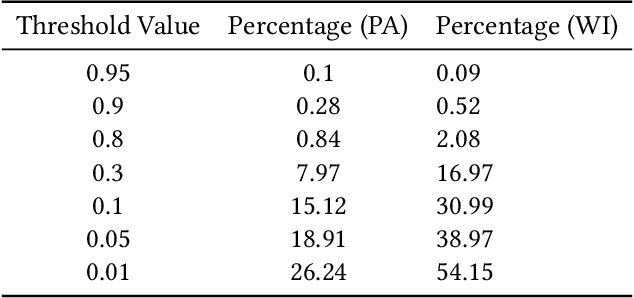
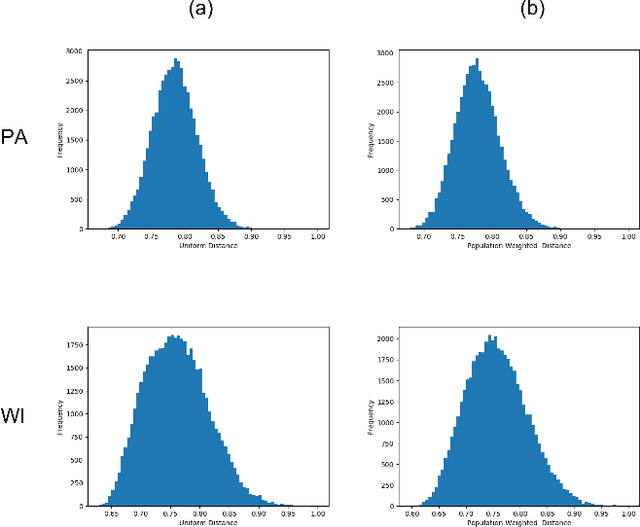
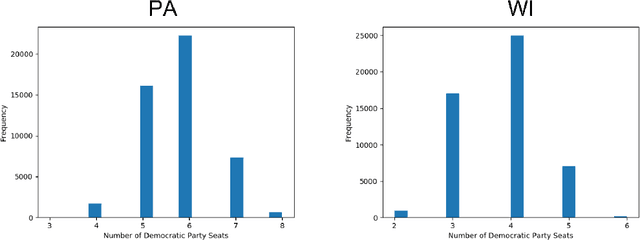
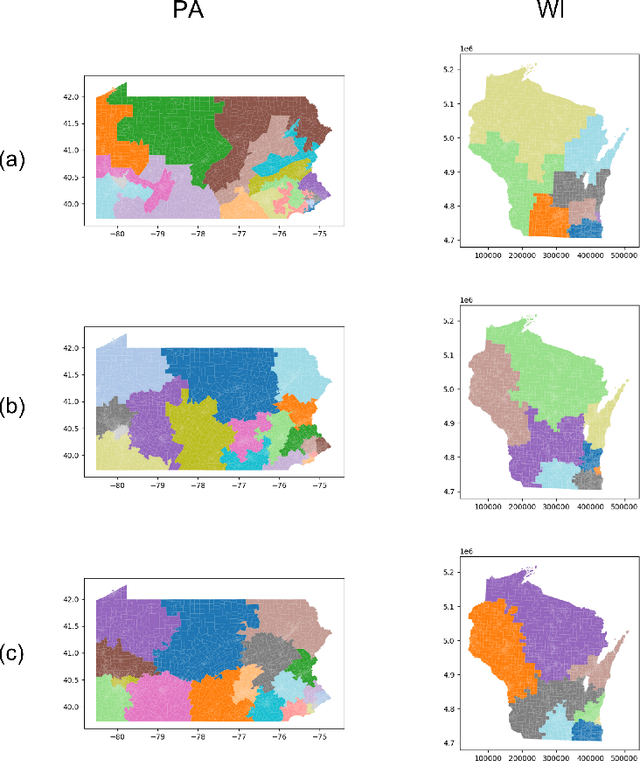
Abstract:In representative democracy, the electorate is often partitioned into districts with each district electing a representative. However, these systems have proven vulnerable to the practice of partisan gerrymandering which involves drawing districts that elect more representatives from a given political party. Additionally, computer-based methods have dramatically enhanced the ability to draw districts that drastically favor one party over others. On the positive side, researchers have recently developed tools for measuring how gerrymandered a redistricting map is by comparing it to a large set of randomly-generated district maps. While these efforts to test whether a district map is "gerrymandered" have achieved real-world impact, the question of how best to draw districts remains very open. Many attempts to automate the redistricting process have been proposed, but not adopted into practice. Typically, they have focused on optimizing certain properties (e.g., geographical compactness or partisan competitiveness of districts) and argued that the properties are desirable. In this work, we take an alternative approach which seeks to find the most "typical" redistricting map. More precisely, we introduce a family of well-motivated distance measures over redistricting maps. Then, by generating a large collection of maps using sampling techniques, we select the map which minimizes the sum of the distances from the collection, i.e., the most "central" map. We produce scalable, linear-time algorithms and derive sample complexity guarantees. Empirically, we show the validity of our algorithms over real world redistricting problems.
Rawlsian Fairness in Online Bipartite Matching: Two-sided, Group, and Individual
Jan 16, 2022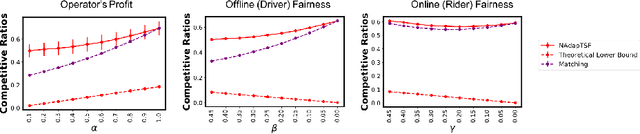
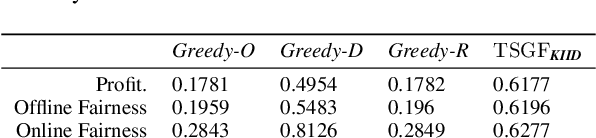
Abstract:Online bipartite-matching platforms are ubiquitous and find applications in important areas such as crowdsourcing and ridesharing. In the most general form, the platform consists of three entities: two sides to be matched and a platform operator that decides the matching. The design of algorithms for such platforms has traditionally focused on the operator's (expected) profit. Recent reports have shown that certain demographic groups may receive less favorable treatment under pure profit maximization. As a result, a collection of online matching algorithms have been developed that give a fair treatment guarantee for one side of the market at the expense of a drop in the operator's profit. In this paper, we generalize the existing work to offer fair treatment guarantees to both sides of the market simultaneously, at a calculated worst case drop to operator profit. We consider group and individual Rawlsian fairness criteria. Moreover, our algorithms have theoretical guarantees and have adjustable parameters that can be tuned as desired to balance the trade-off between the utilities of the three sides. We also derive hardness results that give clear upper bounds over the performance of any algorithm.
Fair Clustering Under a Bounded Cost
Jun 14, 2021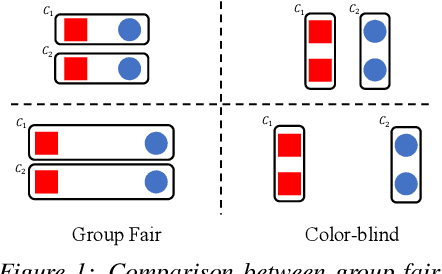
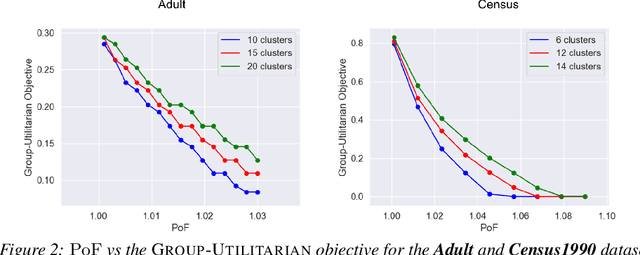
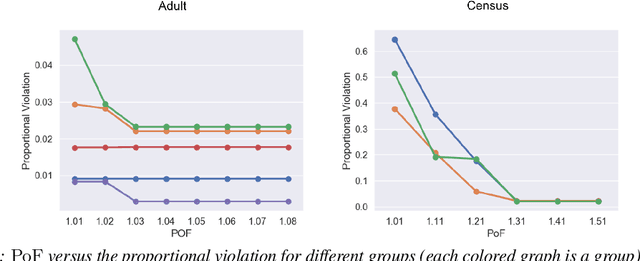
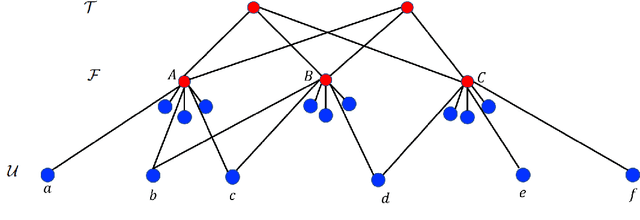
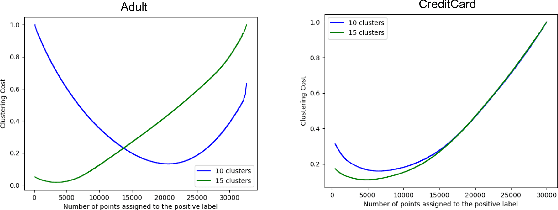
Abstract:Clustering is a fundamental unsupervised learning problem where a dataset is partitioned into clusters that consist of nearby points in a metric space. A recent variant, fair clustering, associates a color with each point representing its group membership and requires that each color has (approximately) equal representation in each cluster to satisfy group fairness. In this model, the cost of the clustering objective increases due to enforcing fairness in the algorithm. The relative increase in the cost, the ''price of fairness,'' can indeed be unbounded. Therefore, in this paper we propose to treat an upper bound on the clustering objective as a constraint on the clustering problem, and to maximize equality of representation subject to it. We consider two fairness objectives: the group utilitarian objective and the group egalitarian objective, as well as the group leximin objective which generalizes the group egalitarian objective. We derive fundamental lower bounds on the approximation of the utilitarian and egalitarian objectives and introduce algorithms with provable guarantees for them. For the leximin objective we introduce an effective heuristic algorithm. We further derive impossibility results for other natural fairness objectives. We conclude with experimental results on real-world datasets that demonstrate the validity of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge