Fair Clustering: Critique, Caveats, and Future Directions

Clustering is a fundamental problem in machine learning and operations research. Therefore, given the fact that fairness considerations have become of paramount importance in algorithm design, fairness in clustering has received significant attention from the research community. The literature on fair clustering has resulted in a collection of interesting fairness notions and elaborate algorithms. In this paper, we take a critical view of fair clustering, identifying a collection of ignored issues such as the lack of a clear utility characterization and the difficulty in accounting for the downstream effects of a fair clustering algorithm in machine learning settings. In some cases, we demonstrate examples where the application of a fair clustering algorithm can have significant negative impacts on social welfare. We end by identifying a collection of steps that would lead towards more impactful research in fair clustering.

Doubly Constrained Fair Clustering

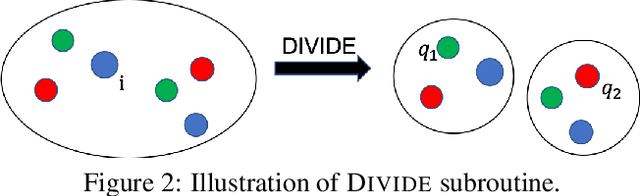
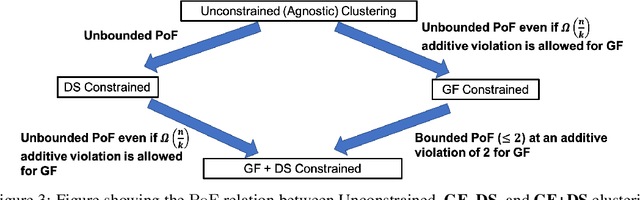
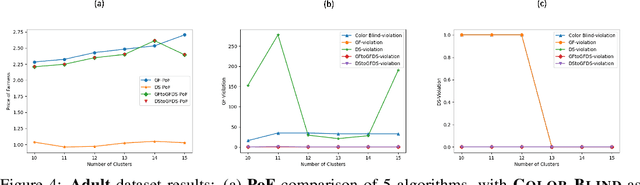
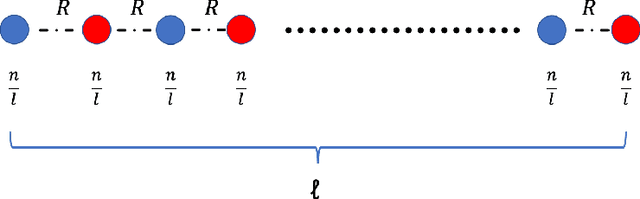
The remarkable attention which fair clustering has received in the last few years has resulted in a significant number of different notions of fairness. Despite the fact that these notions are well-justified, they are often motivated and studied in a disjoint manner where one fairness desideratum is considered exclusively in isolation from the others. This leaves the understanding of the relations between different fairness notions as an important open problem in fair clustering. In this paper, we take the first step in this direction. Specifically, we consider the two most prominent demographic representation fairness notions in clustering: (1) Group Fairness (GF), where the different demographic groups are supposed to have close to population-level representation in each cluster and (2) Diversity in Center Selection (DS), where the selected centers are supposed to have close to population-level representation of each group. We show that given a constant approximation algorithm for one constraint (GF or DS only) we can obtain a constant approximation solution that satisfies both constraints simultaneously. Interestingly, we prove that any given solution that satisfies the GF constraint can always be post-processed at a bounded degradation to the clustering cost to additionally satisfy the DS constraint while the reverse is not true. Furthermore, we show that both GF and DS are incompatible (having an empty feasibility set in the worst case) with a collection of other distance-based fairness notions. Finally, we carry experiments to validate our theoretical findings.