Robust Fair Clustering with Group Membership Uncertainty Sets

We study the canonical fair clustering problem where each cluster is constrained to have close to population-level representation of each group. Despite significant attention, the salient issue of having incomplete knowledge about the group membership of each point has been superficially addressed. In this paper, we consider a setting where errors exist in the assigned group memberships. We introduce a simple and interpretable family of error models that require a small number of parameters to be given by the decision maker. We then present an algorithm for fair clustering with provable robustness guarantees. Our framework enables the decision maker to trade off between the robustness and the clustering quality. Unlike previous work, our algorithms are backed by worst-case theoretical guarantees. Finally, we empirically verify the performance of our algorithm on real world datasets and show its superior performance over existing baselines.

Fair Labeled Clustering

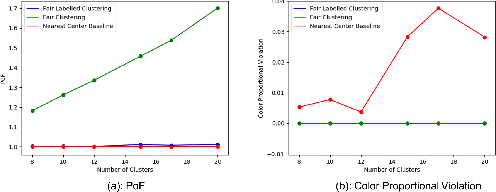
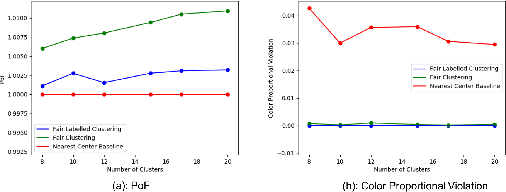
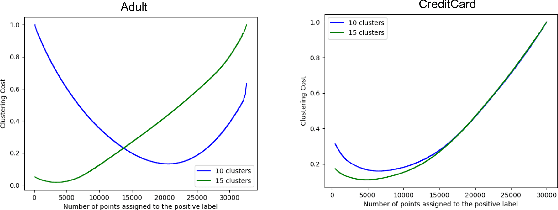
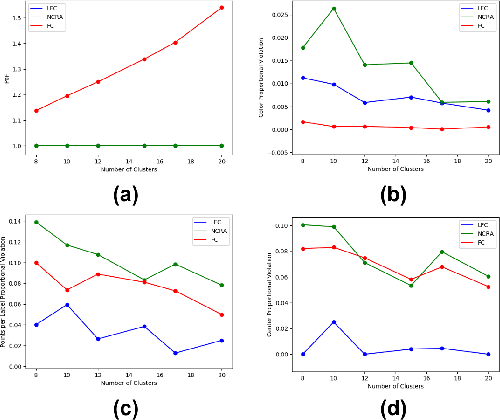
Numerous algorithms have been produced for the fundamental problem of clustering under many different notions of fairness. Perhaps the most common family of notions currently studied is group fairness, in which proportional group representation is ensured in every cluster. We extend this direction by considering the downstream application of clustering and how group fairness should be ensured for such a setting. Specifically, we consider a common setting in which a decision-maker runs a clustering algorithm, inspects the center of each cluster, and decides an appropriate outcome (label) for its corresponding cluster. In hiring for example, there could be two outcomes, positive (hire) or negative (reject), and each cluster would be assigned one of these two outcomes. To ensure group fairness in such a setting, we would desire proportional group representation in every label but not necessarily in every cluster as is done in group fair clustering. We provide algorithms for such problems and show that in contrast to their NP-hard counterparts in group fair clustering, they permit efficient solutions. We also consider a well-motivated alternative setting where the decision-maker is free to assign labels to the clusters regardless of the centers' positions in the metric space. We show that this setting exhibits interesting transitions from computationally hard to easy according to additional constraints on the problem. Moreover, when the constraint parameters take on natural values we show a randomized algorithm for this setting that always achieves an optimal clustering and satisfies the fairness constraints in expectation. Finally, we run experiments on real world datasets that validate the effectiveness of our algorithms.

Rawlsian Fairness in Online Bipartite Matching: Two-sided, Group, and Individual

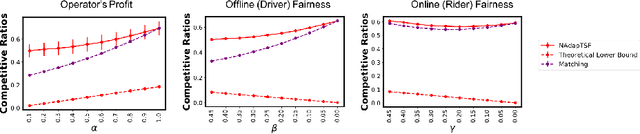
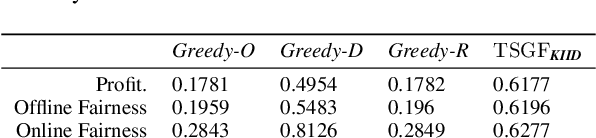
Online bipartite-matching platforms are ubiquitous and find applications in important areas such as crowdsourcing and ridesharing. In the most general form, the platform consists of three entities: two sides to be matched and a platform operator that decides the matching. The design of algorithms for such platforms has traditionally focused on the operator's (expected) profit. Recent reports have shown that certain demographic groups may receive less favorable treatment under pure profit maximization. As a result, a collection of online matching algorithms have been developed that give a fair treatment guarantee for one side of the market at the expense of a drop in the operator's profit. In this paper, we generalize the existing work to offer fair treatment guarantees to both sides of the market simultaneously, at a calculated worst case drop to operator profit. We consider group and individual Rawlsian fairness criteria. Moreover, our algorithms have theoretical guarantees and have adjustable parameters that can be tuned as desired to balance the trade-off between the utilities of the three sides. We also derive hardness results that give clear upper bounds over the performance of any algorithm.