A New Notion of Individually Fair Clustering: $α$-Equitable $k$-Center

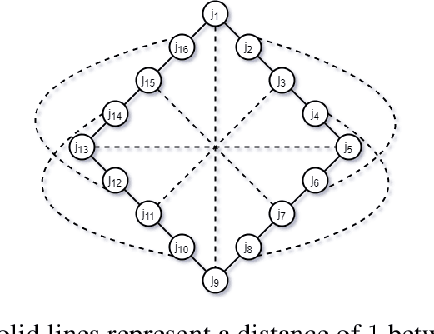
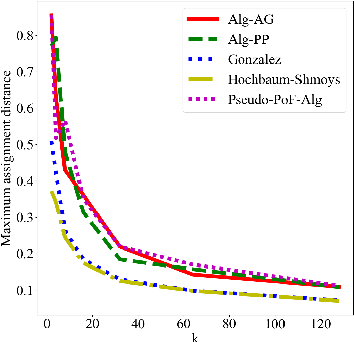
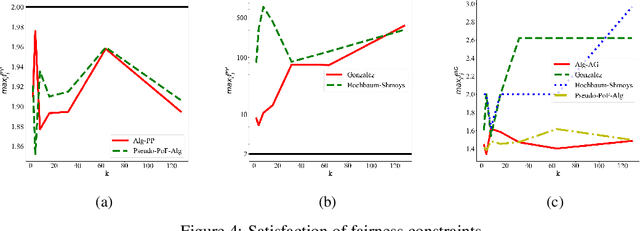
Clustering is a fundamental problem in unsupervised machine learning, and fair variants of it have recently received significant attention. In this work we introduce a novel definition of fairness for clustering problems. Specifically, in our model each point $j$ has a set of other points $\mathcal{S}_j$ that it perceives as similar to itself, and it feels that it is fairly treated, if the quality of service it receives in the solution is $\alpha$-close to that of the points in $\mathcal{S}_j$. We begin our study by answering questions regarding the structure of the problem, namely for what values of $\alpha$ the problem is well-defined, and what the behavior of the Price of Fairness (PoF) for it is. For the well-defined region of $\alpha$, we provide efficient and easily implementable approximation algorithms for the $k$-center objective, which in certain cases also enjoy bounded PoF guarantees. We finally complement our analysis by an extensive suite of experiments that validates the effectiveness of our theoretical results.

Fairness, Semi-Supervised Learning, and More: A General Framework for Clustering with Stochastic Pairwise Constraints

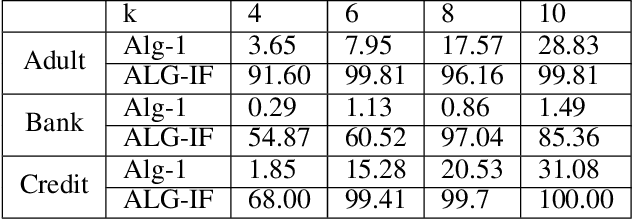
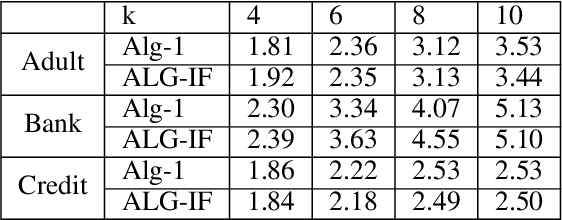
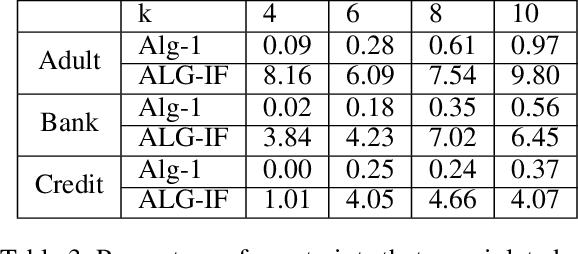
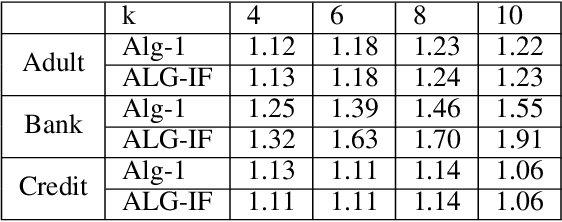
Metric clustering is fundamental in areas ranging from Combinatorial Optimization and Data Mining, to Machine Learning and Operations Research. However, in a variety of situations we may have additional requirements or knowledge, distinct from the underlying metric, regarding which pairs of points should be clustered together. To capture and analyze such scenarios, we introduce a novel family of \emph{stochastic pairwise constraints}, which we incorporate into several essential clustering objectives (radius/median/means). Moreover, we demonstrate that these constraints can succinctly model an intriguing collection of applications, including among others \emph{Individual Fairness} in clustering and \emph{Must-link} constraints in semi-supervised learning. Our main result consists of a general framework that yields approximation algorithms with provable guarantees for important clustering objectives, while at the same time producing solutions that respect the stochastic pairwise constraints. Furthermore, for certain objectives we devise improved results in the case of Must-link constraints, which are also the best possible from a theoretical perspective. Finally, we present experimental evidence that validates the effectiveness of our algorithms.

A Pairwise Fair and Community-preserving Approach to k-Center Clustering

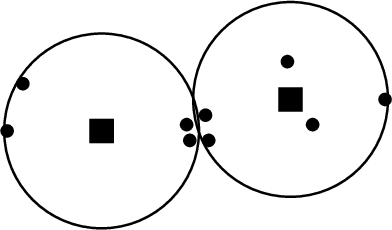
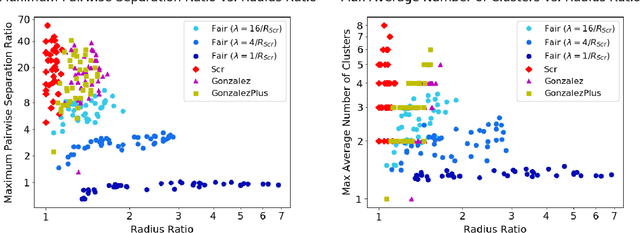
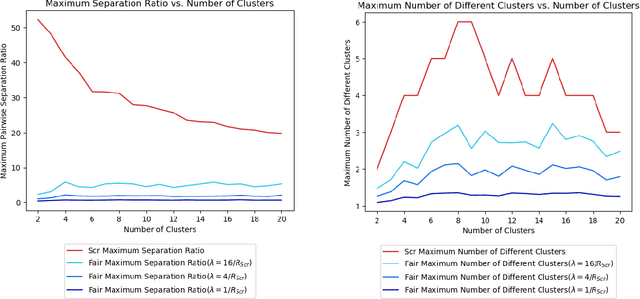
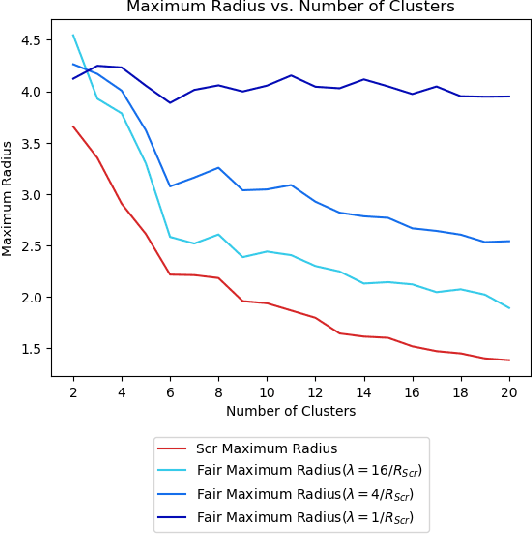
Clustering is a foundational problem in machine learning with numerous applications. As machine learning increases in ubiquity as a backend for automated systems, concerns about fairness arise. Much of the current literature on fairness deals with discrimination against protected classes in supervised learning (group fairness). We define a different notion of fair clustering wherein the probability that two points (or a community of points) become separated is bounded by an increasing function of their pairwise distance (or community diameter). We capture the situation where data points represent people who gain some benefit from being clustered together. Unfairness arises when certain points are deterministically separated, either arbitrarily or by someone who intends to harm them as in the case of gerrymandering election districts. In response, we formally define two new types of fairness in the clustering setting, pairwise fairness and community preservation. To explore the practicality of our fairness goals, we devise an approach for extending existing $k$-center algorithms to satisfy these fairness constraints. Analysis of this approach proves that reasonable approximations can be achieved while maintaining fairness. In experiments, we compare the effectiveness of our approach to classical $k$-center algorithms/heuristics and explore the tradeoff between optimal clustering and fairness.