Tokenized Bandit for LLM Decoding and Alignment

We introduce the tokenized linear bandit (TLB) and multi-armed bandit (TMAB), variants of linear and stochastic multi-armed bandit problems inspired by LLM decoding and alignment. In these problems, at each round $t \in [T]$, a user submits a query (context), and the decision maker (DM) sequentially selects a token irrevocably from a token set. Once the sequence is complete, the DM observes a random utility from the user, whose expectation is presented by a sequence function mapping the chosen token sequence to a nonnegative real value that depends on the query. In both problems, we first show that learning is impossible without any structure on the sequence function. We introduce a natural assumption, diminishing distance with more commons (DDMC), and propose algorithms with regret $\tilde{O}(L\sqrt{T})$ and $\tilde{O}(L\sqrt{T^{2/3}})$ for TLB and TMAB, respectively. As a side product, we obtain an (almost) optimality of the greedy decoding for LLM decoding algorithm under DDMC, which justifies the unresaonable effectiveness of greedy decoding in several tasks. This also has an immediate application to decoding-time LLM alignment, when the misaligned utility can be represented as the frozen LLM's utility and a linearly realizable latent function. We finally validate our algorithm's performance empirically as well as verify our assumptions using synthetic and real-world datasets.

Ad Auctions for LLMs via Retrieval Augmented Generation

In the field of computational advertising, the integration of ads into the outputs of large language models (LLMs) presents an opportunity to support these services without compromising content integrity. This paper introduces novel auction mechanisms for ad allocation and pricing within the textual outputs of LLMs, leveraging retrieval-augmented generation (RAG). We propose a segment auction where an ad is probabilistically retrieved for each discourse segment (paragraph, section, or entire output) according to its bid and relevance, following the RAG framework, and priced according to competing bids. We show that our auction maximizes logarithmic social welfare, a new notion of welfare that balances allocation efficiency and fairness, and we characterize the associated incentive-compatible pricing rule. These results are extended to multi-ad allocation per segment. An empirical evaluation validates the feasibility and effectiveness of our approach over several ad auction scenarios, and exhibits inherent tradeoffs in metrics as we allow the LLM more flexibility to allocate ads.

Dueling Over Dessert, Mastering the Art of Repeated Cake Cutting

We consider the setting of repeated fair division between two players, denoted Alice and Bob, with private valuations over a cake. In each round, a new cake arrives, which is identical to the ones in previous rounds. Alice cuts the cake at a point of her choice, while Bob chooses the left piece or the right piece, leaving the remainder for Alice. We consider two versions: sequential, where Bob observes Alice's cut point before choosing left/right, and simultaneous, where he only observes her cut point after making his choice. The simultaneous version was first considered by Aumann and Maschler (1995). We observe that if Bob is almost myopic and chooses his favorite piece too often, then he can be systematically exploited by Alice through a strategy akin to a binary search. This strategy allows Alice to approximate Bob's preferences with increasing precision, thereby securing a disproportionate share of the resource over time. We analyze the limits of how much a player can exploit the other one and show that fair utility profiles are in fact achievable. Specifically, the players can enforce the equitable utility profile of $(1/2, 1/2)$ in the limit on every trajectory of play, by keeping the other player's utility to approximately $1/2$ on average while guaranteeing they themselves get at least approximately $1/2$ on average. We show this theorem using a connection with Blackwell approachability. Finally, we analyze a natural dynamic known as fictitious play, where players best respond to the empirical distribution of the other player. We show that fictitious play converges to the equitable utility profile of $(1/2, 1/2)$ at a rate of $O(1/\sqrt{T})$.

Replication-proof Bandit Mechanism Design

We study a problem of designing replication-proof bandit mechanisms when agents strategically register or replicate their own arms to maximize their payoff. We consider Bayesian agents who are unaware of ex-post realization of their own arms' mean rewards, which is the first to study Bayesian extension of Shin et al. (2022). This extension presents significant challenges in analyzing equilibrium, in contrast to the fully-informed setting by Shin et al. (2022) under which the problem simply reduces to a case where each agent only has a single arm. With Bayesian agents, even in a single-agent setting, analyzing the replication-proofness of an algorithm becomes complicated. Remarkably, we first show that the algorithm proposed by Shin et al. (2022), defined H-UCB, is no longer replication-proof for any exploration parameters. Then, we provide sufficient and necessary conditions for an algorithm to be replication-proof in the single-agent setting. These results centers around several analytical results in comparing the expected regret of multiple bandit instances, which might be of independent interest. We further prove that exploration-then-commit (ETC) algorithm satisfies these properties, whereas UCB does not, which in fact leads to the failure of being replication-proof. We expand this result to multi-agent setting, and provide a replication-proof algorithm for any problem instance. The proof mainly relies on the single-agent result, as well as some structural properties of ETC and the novel introduction of a restarting round, which largely simplifies the analysis while maintaining the regret unchanged (up to polylogarithmic factor). We finalize our result by proving its sublinear regret upper bound, which matches that of H-UCB.

Robust and Performance Incentivizing Algorithms for Multi-Armed Bandits with Strategic Agents

We consider a variant of the stochastic multi-armed bandit problem. Specifically, the arms are strategic agents who can improve their rewards or absorb them. The utility of an agent increases if she is pulled more or absorbs more of her rewards but decreases if she spends more effort improving her rewards. Agents have heterogeneous properties, specifically having different means and able to improve their rewards up to different levels. Further, a non-empty subset of agents are ''honest'' and in the worst case always give their rewards without absorbing any part. The principal wishes to obtain a high revenue (cumulative reward) by designing a mechanism that incentives top level performance at equilibrium. At the same time, the principal wishes to be robust and obtain revenue at least at the level of the honest agent with the highest mean in case of non-equilibrium behaviour. We identify a class of MAB algorithms which we call performance incentivizing which satisfy a collection of properties and show that they lead to mechanisms that incentivize top level performance at equilibrium and are robust under any strategy profile. Interestingly, we show that UCB is an example of such a MAB algorithm. Further, in the case where the top performance level is unknown we show that combining second price auction ideas with performance incentivizing algorithms achieves performance at least at the second top level while also being robust.

Online Advertisements with LLMs: Opportunities and Challenges

This paper explores the potential for leveraging Large Language Models (LLM) in the realm of online advertising systems. We delve into essential requirements including privacy, latency, reliability, users and advertisers' satisfaction, which such a system must fulfill. We further introduce a general framework for LLM advertisement, consisting of modification, bidding, prediction, and auction modules. Different design considerations for each module is presented, with an in-depth examination of their practicality and the technical challenges inherent to their implementation.

An Improved Relaxation for Oracle-Efficient Adversarial Contextual Bandits

We present an oracle-efficient relaxation for the adversarial contextual bandits problem, where the contexts are sequentially drawn i.i.d from a known distribution and the cost sequence is chosen by an online adversary. Our algorithm has a regret bound of $O(T^{\frac{2}{3}}(K\log(|\Pi|))^{\frac{1}{3}})$ and makes at most $O(K)$ calls per round to an offline optimization oracle, where $K$ denotes the number of actions, $T$ denotes the number of rounds and $\Pi$ denotes the set of policies. This is the first result to improve the prior best bound of $O((TK)^{\frac{2}{3}}(\log(|\Pi|))^{\frac{1}{3}})$ as obtained by Syrgkanis et al. at NeurIPS 2016, and the first to match the original bound of Langford and Zhang at NeurIPS 2007 which was obtained for the stochastic case.

Regret Analysis of Repeated Delegated Choice

We present a study on a repeated delegated choice problem, which is the first to consider an online learning variant of Kleinberg and Kleinberg, EC'18. In this model, a principal interacts repeatedly with an agent who possesses an exogenous set of solutions to search for efficient ones. Each solution can yield varying utility for both the principal and the agent, and the agent may propose a solution to maximize its own utility in a selfish manner. To mitigate this behavior, the principal announces an eligible set which screens out a certain set of solutions. The principal, however, does not have any information on the distribution of solutions in advance. Therefore, the principal dynamically announces various eligible sets to efficiently learn the distribution. The principal's objective is to minimize cumulative regret compared to the optimal eligible set in hindsight. We explore two dimensions of the problem setup, whether the agent behaves myopically or strategizes across the rounds, and whether the solutions yield deterministic or stochastic utility. Our analysis mainly characterizes some regimes under which the principal can recover the sublinear regret, thereby shedding light on the rise and fall of the repeated delegation procedure in various regimes.

Bandit Social Learning: Exploration under Myopic Behavior

We study social learning dynamics where the agents collectively follow a simple multi-armed bandit protocol. Agents arrive sequentially, choose arms and receive associated rewards. Each agent observes the full history (arms and rewards) of the previous agents, and there are no private signals. While collectively the agents face exploration-exploitation tradeoff, each agent acts myopically, without regards to exploration. Motivating scenarios concern reviews and ratings on online platforms. We allow a wide range of myopic behaviors that are consistent with (parameterized) confidence intervals, including the "unbiased" behavior as well as various behaviorial biases. While extreme versions of these behaviors correspond to well-known bandit algorithms, we prove that more moderate versions lead to stark exploration failures, and consequently to regret rates that are linear in the number of agents. We provide matching upper bounds on regret by analyzing "moderately optimistic" agents. As a special case of independent interest, we obtain a general result on failure of the greedy algorithm in multi-armed bandits. This is the first such result in the literature, to the best of our knowledge

Multi-armed Bandit Algorithm against Strategic Replication

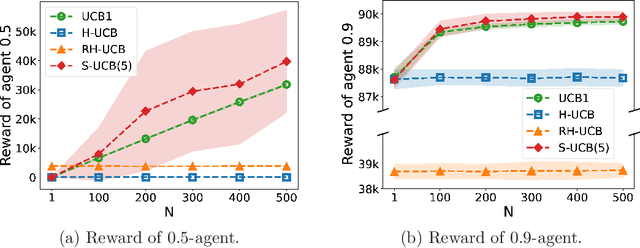
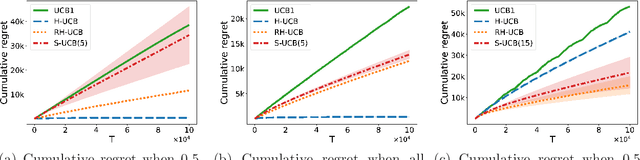
We consider a multi-armed bandit problem in which a set of arms is registered by each agent, and the agent receives reward when its arm is selected. An agent might strategically submit more arms with replications, which can bring more reward by abusing the bandit algorithm's exploration-exploitation balance. Our analysis reveals that a standard algorithm indeed fails at preventing replication and suffers from linear regret in time $T$. We aim to design a bandit algorithm which demotivates replications and also achieves a small cumulative regret. We devise Hierarchical UCB (H-UCB) of replication-proof, which has $O(\ln T)$-regret under any equilibrium. We further propose Robust Hierarchical UCB (RH-UCB) which has a sublinear regret even in a realistic scenario with irrational agents replicating careless. We verify our theoretical findings through numerical experiments.