Active Preference-based Learning for Multi-dimensional Personalization

Large language models (LLMs) have shown remarkable versatility across tasks, but aligning them with individual human preferences remains challenging due to the complexity and diversity of these preferences. Existing methods often overlook the fact that preferences are multi-objective, diverse, and hard to articulate, making full alignment difficult. In response, we propose an active preference learning framework that uses binary feedback to estimate user preferences across multiple objectives. Our approach leverages Bayesian inference to update preferences efficiently and reduces user feedback through an acquisition function that optimally selects queries. Additionally, we introduce a parameter to handle feedback noise and improve robustness. We validate our approach through theoretical analysis and experiments on language generation tasks, demonstrating its feedback efficiency and effectiveness in personalizing model responses.

Multi-Agent Path Finding with Real Robot Dynamics and Interdependent Tasks for Automated Warehouses

Multi-Agent Path Finding (MAPF) is an important optimization problem underlying the deployment of robots in automated warehouses and factories. Despite the large body of work on this topic, most approaches make heavy simplifications, both on the environment and the agents, which make the resulting algorithms impractical for real-life scenarios. In this paper, we consider a realistic problem of online order delivery in a warehouse, where a fleet of robots bring the products belonging to each order from shelves to workstations. This creates a stream of inter-dependent pickup and delivery tasks and the associated MAPF problem consists of computing realistic collision-free robot trajectories fulfilling these tasks. To solve this MAPF problem, we propose an extension of the standard Prioritized Planning algorithm to deal with the inter-dependent tasks (Interleaved Prioritized Planning) and a novel Via-Point Star (VP*) algorithm to compute an optimal dynamics-compliant robot trajectory to visit a sequence of goal locations while avoiding moving obstacles. We prove the completeness of our approach and evaluate it in simulation as well as in a real warehouse.

Using Linearized Optimal Transport to Predict the Evolution of Stochastic Particle Systems

We develop an algorithm to approximate the time evolution of a probability measure without explicitly learning an operator that governs the evolution. A particular application of interest is discrete measures $\mu_t^N$ that arise from particle systems. In many such situations, the individual particles move chaotically on short time scales, making it difficult to learn the dynamics of a governing operator, but the bulk distribution $\mu_t^N$ approximates an absolutely continuous measure $\mu_t$ that evolves ``smoothly.'' If $\mu_t$ is known on some time interval, then linearized optimal transport theory provides an Euler-like scheme for approximating the evolution of $\mu_t$ using its ``tangent vector field'' (represented as a time-dependent vector field on $\mathbb R^d$), which can be computed as a limit of optimal transport maps. We propose an analog of this Euler approximation to predict the evolution of the discrete measure $\mu_t^N$ (without knowing $\mu_t$). To approximate the analogous tangent vector field, we use a finite difference over a time step that sits between the two time scales of the system -- long enough for the large-$N$ evolution ($\mu_t$) to emerge but short enough to satisfactorily approximate the derivative object used in the Euler scheme. By allowing the limiting behavior to emerge, the optimal transport maps closely approximate the vector field describing the bulk distribution's smooth evolution instead of the individual particles' more chaotic movements. We demonstrate the efficacy of this approach with two illustrative examples, Gaussian diffusion and a cell chemotaxis model, and show that our method succeeds in predicting the bulk behavior over relatively large steps.

Learning black- and gray-box chemotactic PDEs/closures from agent based Monte Carlo simulation data

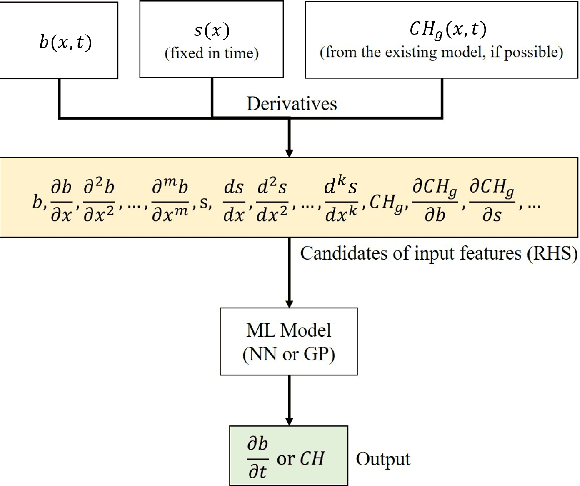
We propose a machine learning framework for the data-driven discovery of macroscopic chemotactic Partial Differential Equations (PDEs) -- and the closures that lead to them -- from high-fidelity, individual-based stochastic simulations of E.coli bacterial motility. The fine scale, detailed, hybrid (continuum - Monte Carlo) simulation model embodies the underlying biophysics, and its parameters are informed from experimental observations of individual cells. We exploit Automatic Relevance Determination (ARD) within a Gaussian Process framework for the identification of a parsimonious set of collective observables that parametrize the law of the effective PDEs. Using these observables, in a second step we learn effective, coarse-grained "Keller-Segel class" chemotactic PDEs using machine learning regressors: (a) (shallow) feedforward neural networks and (b) Gaussian Processes. The learned laws can be black-box (when no prior knowledge about the PDE law structure is assumed) or gray-box when parts of the equation (e.g. the pure diffusion part) is known and "hardwired" in the regression process. We also discuss data-driven corrections (both additive and functional) of analytically known, approximate closures.

Multi-armed Bandit Algorithm against Strategic Replication

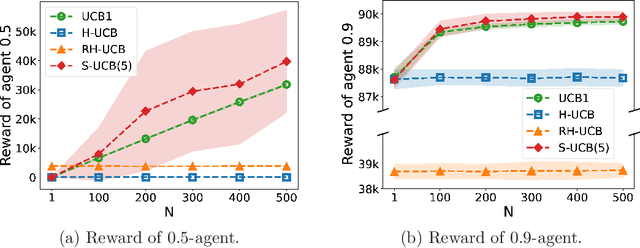
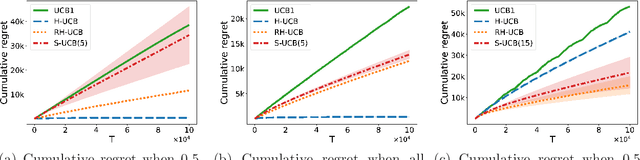
We consider a multi-armed bandit problem in which a set of arms is registered by each agent, and the agent receives reward when its arm is selected. An agent might strategically submit more arms with replications, which can bring more reward by abusing the bandit algorithm's exploration-exploitation balance. Our analysis reveals that a standard algorithm indeed fails at preventing replication and suffers from linear regret in time $T$. We aim to design a bandit algorithm which demotivates replications and also achieves a small cumulative regret. We devise Hierarchical UCB (H-UCB) of replication-proof, which has $O(\ln T)$-regret under any equilibrium. We further propose Robust Hierarchical UCB (RH-UCB) which has a sublinear regret even in a realistic scenario with irrational agents replicating careless. We verify our theoretical findings through numerical experiments.

Coarse-scale PDEs from fine-scale observations via machine learning

Complex spatiotemporal dynamics of physicochemical processes are often modeled at a microscopic level (through e.g. atomistic, agent-based or lattice models) based on first principles. Some of these processes can also be successfully modeled at the macroscopic level using e.g. partial differential equations (PDEs) describing the evolution of the right few macroscopic observables (e.g. concentration and momentum fields). Deriving good macroscopic descriptions (the so-called "closure problem") is often a time-consuming process requiring deep understanding/intuition about the system of interest. Recent developments in data science provide alternative ways to effectively extract/learn accurate macroscopic descriptions approximating the underlying microscopic observations. In this paper, we introduce a data-driven framework for the identification of unavailable coarse-scale PDEs from microscopic observations via machine learning algorithms. Specifically, using Gaussian Processes, Artificial Neural Networks, and/or Diffusion Maps, the proposed framework uncovers the relation between the relevant macroscopic space fields and their time evolution (the right-hand-side of the explicitly unavailable macroscopic PDE). Interestingly, several choices equally representative of the data can be discovered. The framework will be illustrated through the data-driven discovery of macroscopic, concentration-level PDEs resulting from a fine-scale, Lattice Boltzmann level model of a reaction/transport process. Once the coarse evolution law is identified, it can be simulated to produce long-term macroscopic predictions. Different features (pros as well as cons) of alternative machine learning algorithms for performing this task (Gaussian Processes and Artificial Neural Networks), are presented and discussed.

Linking Gaussian Process regression with data-driven manifold embeddings for nonlinear data fusion

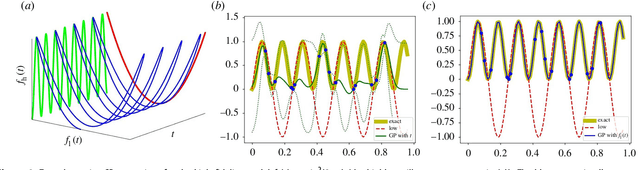
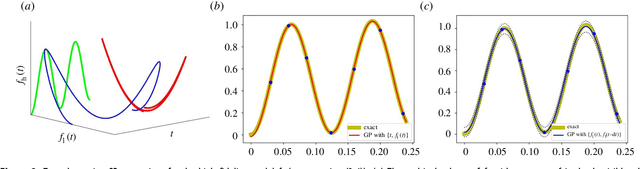
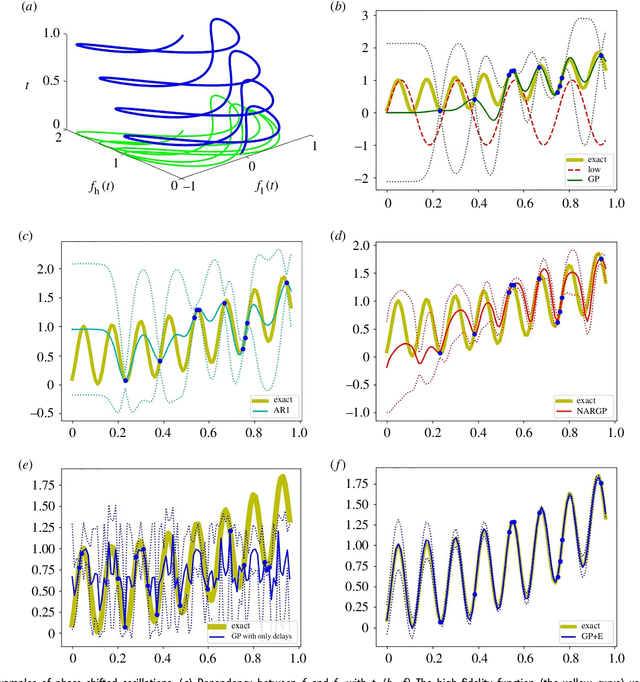
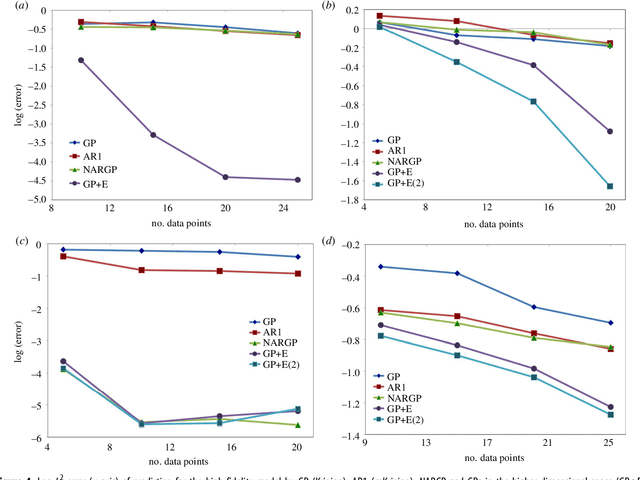
In statistical modeling with Gaussian Process regression, it has been shown that combining (few) high-fidelity data with (many) low-fidelity data can enhance prediction accuracy, compared to prediction based on the few high-fidelity data only. Such information fusion techniques for multifidelity data commonly approach the high-fidelity model $f_h(t)$ as a function of two variables $(t,y)$, and then using $f_l(t)$ as the $y$ data. More generally, the high-fidelity model can be written as a function of several variables $(t,y_1,y_2....)$; the low-fidelity model $f_l$ and, say, some of its derivatives, can then be substituted for these variables. In this paper, we will explore mathematical algorithms for multifidelity information fusion that use such an approach towards improving the representation of the high-fidelity function with only a few training data points. Given that $f_h$ may not be a simple function -- and sometimes not even a function -- of $f_l$, we demonstrate that using additional functions of $t$, such as derivatives or shifts of $f_l$, can drastically improve the approximation of $f_h$ through Gaussian Processes. We also point out a connection with "embedology" techniques from topology and dynamical systems.