Active search for Bifurcations

Bifurcations mark qualitative changes of long-term behavior in dynamical systems and can often signal sudden ("hard") transitions or catastrophic events (divergences). Accurately locating them is critical not just for deeper understanding of observed dynamic behavior, but also for designing efficient interventions. When the dynamical system at hand is complex, possibly noisy, and expensive to sample, standard (e.g. continuation based) numerical methods may become impractical. We propose an active learning framework, where Bayesian Optimization is leveraged to discover saddle-node or Hopf bifurcations, from a judiciously chosen small number of vector field observations. Such an approach becomes especially attractive in systems whose state x parameter space exploration is resource-limited. It also naturally provides a framework for uncertainty quantification (aleatoric and epistemic), useful in systems with inherent stochasticity.

Limits of Entrainment of Circadian Neuronal Networks

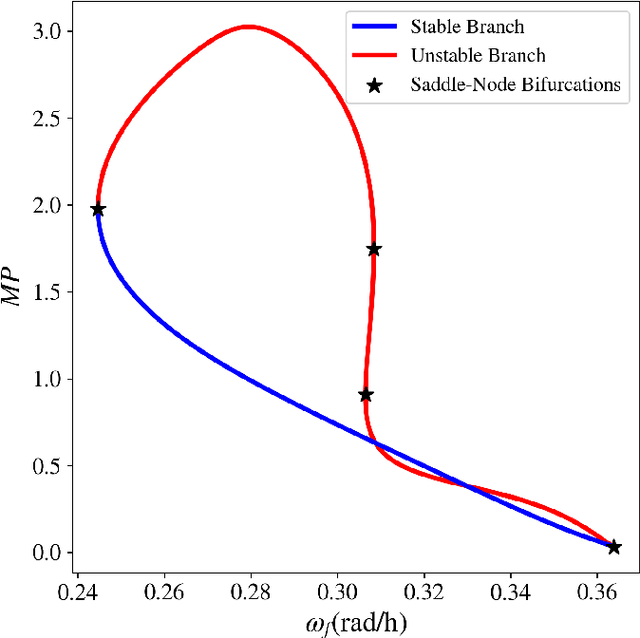
Circadian rhythmicity lies at the center of various important physiological and behavioral processes in mammals, such as sleep, metabolism, homeostasis, mood changes and more. It has been shown that this rhythm arises from self-sustained biomolecular oscillations of a neuronal network located in the Suprachiasmatic Nucleus (SCN). Under normal circumstances, this network remains synchronized to the day-night cycle due to signaling from the retina. Misalignment of these neuronal oscillations with the external light signal can disrupt numerous physiological functions and take a long-lasting toll on health and well-being. In this work, we study a modern computational neuroscience model to determine the limits of circadian synchronization to external light signals of different frequency and duty cycle. We employ a matrix-free approach to locate periodic steady states of the high-dimensional model for various driving conditions. Our algorithmic pipeline enables numerical continuation and construction of bifurcation diagrams w.r.t. forcing parameters. We computationally explore the effect of heterogeneity in the circadian neuronal network, as well as the effect of corrective therapeutic interventions, such as that of the drug molecule Longdaysin. Lastly, we employ unsupervised learning to construct a data-driven embedding space for representing neuronal heterogeneity.

Learning black- and gray-box chemotactic PDEs/closures from agent based Monte Carlo simulation data

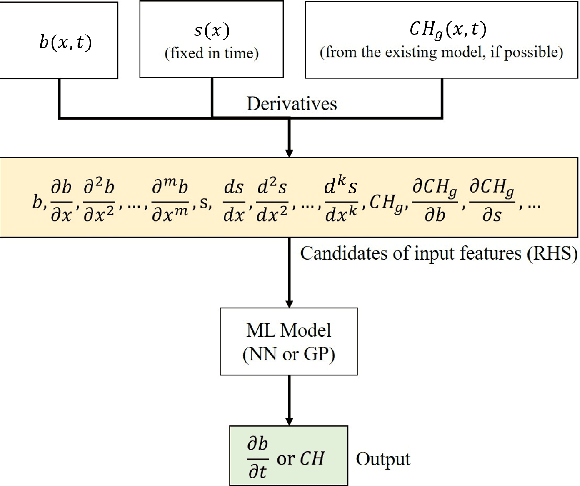
We propose a machine learning framework for the data-driven discovery of macroscopic chemotactic Partial Differential Equations (PDEs) -- and the closures that lead to them -- from high-fidelity, individual-based stochastic simulations of E.coli bacterial motility. The fine scale, detailed, hybrid (continuum - Monte Carlo) simulation model embodies the underlying biophysics, and its parameters are informed from experimental observations of individual cells. We exploit Automatic Relevance Determination (ARD) within a Gaussian Process framework for the identification of a parsimonious set of collective observables that parametrize the law of the effective PDEs. Using these observables, in a second step we learn effective, coarse-grained "Keller-Segel class" chemotactic PDEs using machine learning regressors: (a) (shallow) feedforward neural networks and (b) Gaussian Processes. The learned laws can be black-box (when no prior knowledge about the PDE law structure is assumed) or gray-box when parts of the equation (e.g. the pure diffusion part) is known and "hardwired" in the regression process. We also discuss data-driven corrections (both additive and functional) of analytically known, approximate closures.