Learning black- and gray-box chemotactic PDEs/closures from agent based Monte Carlo simulation data

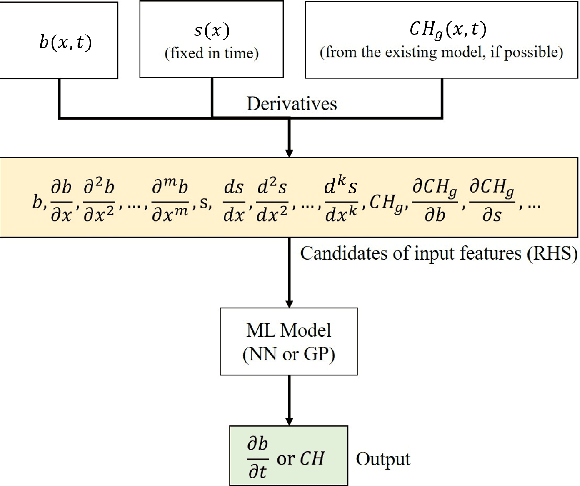
We propose a machine learning framework for the data-driven discovery of macroscopic chemotactic Partial Differential Equations (PDEs) -- and the closures that lead to them -- from high-fidelity, individual-based stochastic simulations of E.coli bacterial motility. The fine scale, detailed, hybrid (continuum - Monte Carlo) simulation model embodies the underlying biophysics, and its parameters are informed from experimental observations of individual cells. We exploit Automatic Relevance Determination (ARD) within a Gaussian Process framework for the identification of a parsimonious set of collective observables that parametrize the law of the effective PDEs. Using these observables, in a second step we learn effective, coarse-grained "Keller-Segel class" chemotactic PDEs using machine learning regressors: (a) (shallow) feedforward neural networks and (b) Gaussian Processes. The learned laws can be black-box (when no prior knowledge about the PDE law structure is assumed) or gray-box when parts of the equation (e.g. the pure diffusion part) is known and "hardwired" in the regression process. We also discuss data-driven corrections (both additive and functional) of analytically known, approximate closures.

Coarse-scale PDEs from fine-scale observations via machine learning

Complex spatiotemporal dynamics of physicochemical processes are often modeled at a microscopic level (through e.g. atomistic, agent-based or lattice models) based on first principles. Some of these processes can also be successfully modeled at the macroscopic level using e.g. partial differential equations (PDEs) describing the evolution of the right few macroscopic observables (e.g. concentration and momentum fields). Deriving good macroscopic descriptions (the so-called "closure problem") is often a time-consuming process requiring deep understanding/intuition about the system of interest. Recent developments in data science provide alternative ways to effectively extract/learn accurate macroscopic descriptions approximating the underlying microscopic observations. In this paper, we introduce a data-driven framework for the identification of unavailable coarse-scale PDEs from microscopic observations via machine learning algorithms. Specifically, using Gaussian Processes, Artificial Neural Networks, and/or Diffusion Maps, the proposed framework uncovers the relation between the relevant macroscopic space fields and their time evolution (the right-hand-side of the explicitly unavailable macroscopic PDE). Interestingly, several choices equally representative of the data can be discovered. The framework will be illustrated through the data-driven discovery of macroscopic, concentration-level PDEs resulting from a fine-scale, Lattice Boltzmann level model of a reaction/transport process. Once the coarse evolution law is identified, it can be simulated to produce long-term macroscopic predictions. Different features (pros as well as cons) of alternative machine learning algorithms for performing this task (Gaussian Processes and Artificial Neural Networks), are presented and discussed.