A Mechanistic Analysis of Transformers for Dynamical Systems

Transformers are increasingly adopted for modeling and forecasting time-series, yet their internal mechanisms remain poorly understood from a dynamical systems perspective. In contrast to classical autoregressive and state-space models, which benefit from well-established theoretical foundations, Transformer architectures are typically treated as black boxes. This gap becomes particularly relevant as attention-based models are considered for general-purpose or zero-shot forecasting across diverse dynamical regimes. In this work, we do not propose a new forecasting model, but instead investigate the representational capabilities and limitations of single-layer Transformers when applied to dynamical data. Building on a dynamical systems perspective we interpret causal self-attention as a linear, history-dependent recurrence and analyze how it processes temporal information. Through a series of linear and nonlinear case studies, we identify distinct operational regimes. For linear systems, we show that the convexity constraint imposed by softmax attention fundamentally restricts the class of dynamics that can be represented, leading to oversmoothing in oscillatory settings. For nonlinear systems under partial observability, attention instead acts as an adaptive delay-embedding mechanism, enabling effective state reconstruction when sufficient temporal context and latent dimensionality are available. These results help bridge empirical observations with classical dynamical systems theory, providing insight into when and why Transformers succeed or fail as models of dynamical systems.

BumpNet: A Sparse Neural Network Framework for Learning PDE Solutions

We introduce BumpNet, a sparse neural network framework for PDE numerical solution and operator learning. BumpNet is based on meshless basis function expansion, in a similar fashion to radial-basis function (RBF) networks. Unlike RBF networks, the basis functions in BumpNet are constructed from ordinary sigmoid activation functions. This enables the efficient use of modern training techniques optimized for such networks. All parameters of the basis functions, including shape, location, and amplitude, are fully trainable. Model parsimony and h-adaptivity are effectively achieved through dynamically pruning basis functions during training. BumpNet is a general framework that can be combined with existing neural architectures for learning PDE solutions: here, we propose Bump-PINNs (BumpNet with physics-informed neural networks) for solving general PDEs; Bump-EDNN (BumpNet with evolutionary deep neural networks) to solve time-evolution PDEs; and Bump-DeepONet (BumpNet with deep operator networks) for PDE operator learning. Bump-PINNs are trained using the same collocation-based approach used by PINNs, Bump-EDNN uses a BumpNet only in the spatial domain and uses EDNNs to advance the solution in time, while Bump-DeepONets employ a BumpNet regression network as the trunk network of a DeepONet. Extensive numerical experiments demonstrate the efficiency and accuracy of the proposed architecture.

Enabling Local Neural Operators to perform Equation-Free System-Level Analysis

Neural Operators (NOs) provide a powerful framework for computations involving physical laws that can be modelled by (integro-) partial differential equations (PDEs), directly learning maps between infinite-dimensional function spaces that bypass both the explicit equation identification and their subsequent numerical solving. Still, NOs have so far primarily been employed to explore the dynamical behavior as surrogates of brute-force temporal simulations/predictions. Their potential for systematic rigorous numerical system-level tasks, such as fixed-point, stability, and bifurcation analysis - crucial for predicting irreversible transitions in real-world phenomena - remains largely unexplored. Toward this aim, inspired by the Equation-Free multiscale framework, we propose and implement a framework that integrates (local) NOs with advanced iterative numerical methods in the Krylov subspace, so as to perform efficient system-level stability and bifurcation analysis of large-scale dynamical systems. Beyond fixed point, stability, and bifurcation analysis enabled by local in time NOs, we also demonstrate the usefulness of local in space as well as in space-time ("patch") NOs in accelerating the computer-aided analysis of spatiotemporal dynamics. We illustrate our framework via three nonlinear PDE benchmarks: the 1D Allen-Cahn equation, which undergoes multiple concatenated pitchfork bifurcations; the Liouville-Bratu-Gelfand PDE, which features a saddle-node tipping point; and the FitzHugh-Nagumo (FHN) model, consisting of two coupled PDEs that exhibit both Hopf and saddle-node bifurcations.

Generative Learning for Slow Manifolds and Bifurcation Diagrams

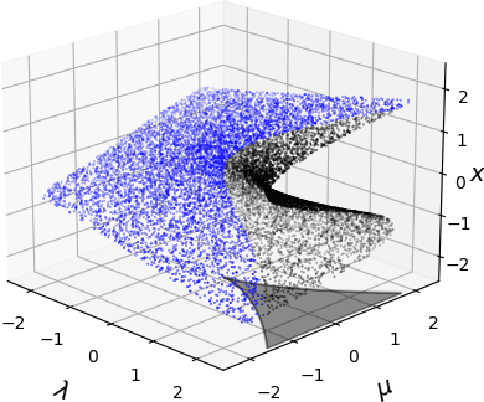
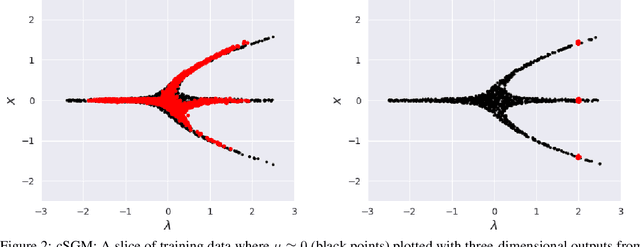
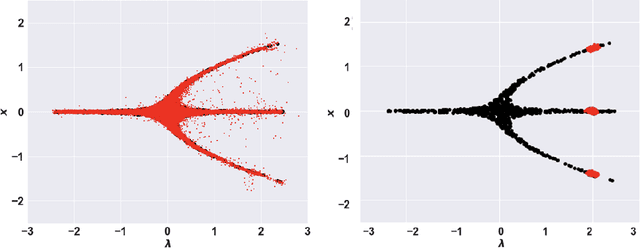
In dynamical systems characterized by separation of time scales, the approximation of so called ``slow manifolds'', on which the long term dynamics lie, is a useful step for model reduction. Initializing on such slow manifolds is a useful step in modeling, since it circumvents fast transients, and is crucial in multiscale algorithms alternating between fine scale (fast) and coarser scale (slow) simulations. In a similar spirit, when one studies the infinite time dynamics of systems depending on parameters, the system attractors (e.g., its steady states) lie on bifurcation diagrams. Sampling these manifolds gives us representative attractors (here, steady states of ODEs or PDEs) at different parameter values. Algorithms for the systematic construction of these manifolds are required parts of the ``traditional'' numerical nonlinear dynamics toolkit. In more recent years, as the field of Machine Learning develops, conditional score-based generative models (cSGMs) have demonstrated capabilities in generating plausible data from target distributions that are conditioned on some given label. It is tempting to exploit such generative models to produce samples of data distributions conditioned on some quantity of interest (QoI). In this work, we present a framework for using cSGMs to quickly (a) initialize on a low-dimensional (reduced-order) slow manifold of a multi-time-scale system consistent with desired value(s) of a QoI (a ``label'') on the manifold, and (b) approximate steady states in a bifurcation diagram consistent with a (new, out-of-sample) parameter value. This conditional sampling can help uncover the geometry of the reduced slow-manifold and/or approximately ``fill in'' missing segments of steady states in a bifurcation diagram.

Neural Chaos: A Spectral Stochastic Neural Operator

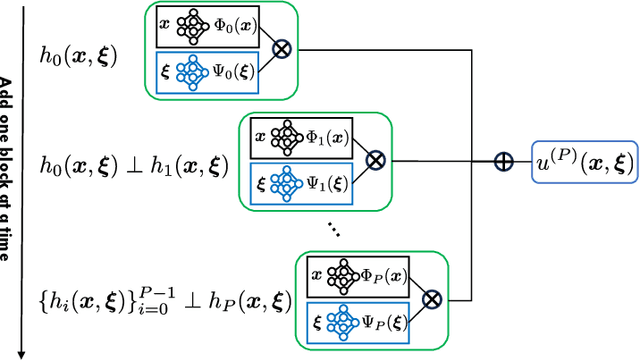
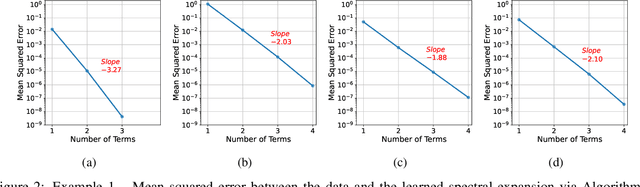
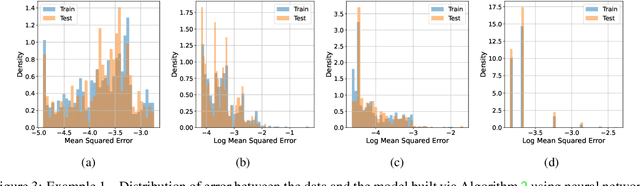
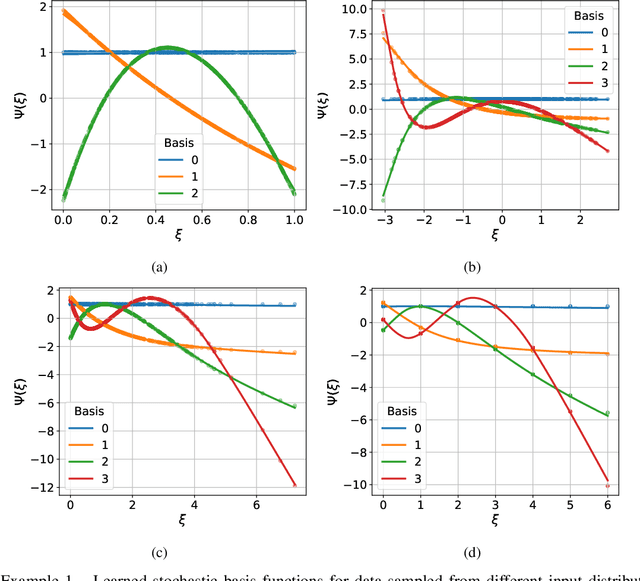
Building surrogate models with uncertainty quantification capabilities is essential for many engineering applications where randomness, such as variability in material properties, is unavoidable. Polynomial Chaos Expansion (PCE) is widely recognized as a to-go method for constructing stochastic solutions in both intrusive and non-intrusive ways. Its application becomes challenging, however, with complex or high-dimensional processes, as achieving accuracy requires higher-order polynomials, which can increase computational demands and or the risk of overfitting. Furthermore, PCE requires specialized treatments to manage random variables that are not independent, and these treatments may be problem-dependent or may fail with increasing complexity. In this work, we adopt the spectral expansion formalism used in PCE; however, we replace the classical polynomial basis functions with neural network (NN) basis functions to leverage their expressivity. To achieve this, we propose an algorithm that identifies NN-parameterized basis functions in a purely data-driven manner, without any prior assumptions about the joint distribution of the random variables involved, whether independent or dependent. The proposed algorithm identifies each NN-parameterized basis function sequentially, ensuring they are orthogonal with respect to the data distribution. The basis functions are constructed directly on the joint stochastic variables without requiring a tensor product structure. This approach may offer greater flexibility for complex stochastic models, while simplifying implementation compared to the tensor product structures typically used in PCE to handle random vectors. We demonstrate the effectiveness of the proposed scheme through several numerical examples of varying complexity and provide comparisons with classical PCE.

Comparing analytic and data-driven approaches to parameter identifiability: A power systems case study

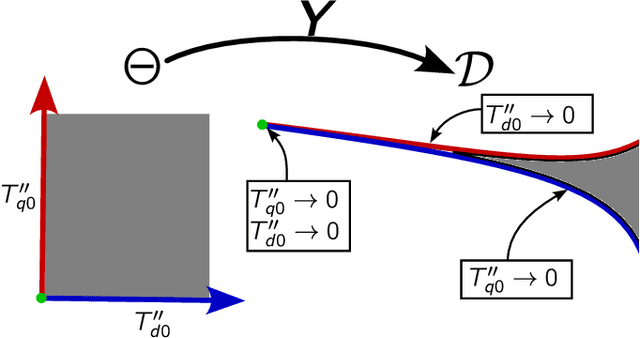
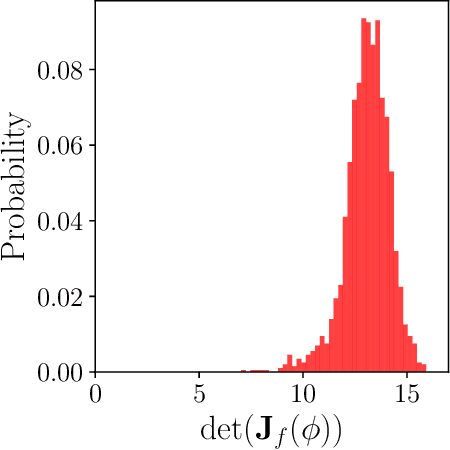
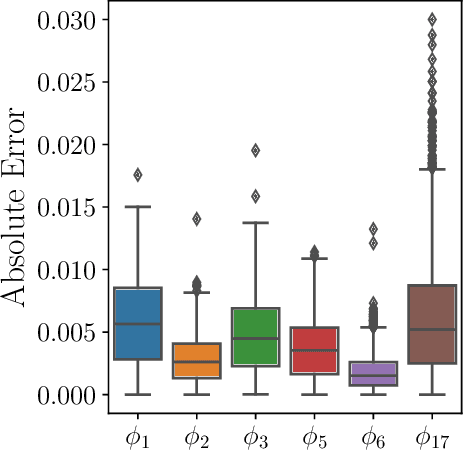
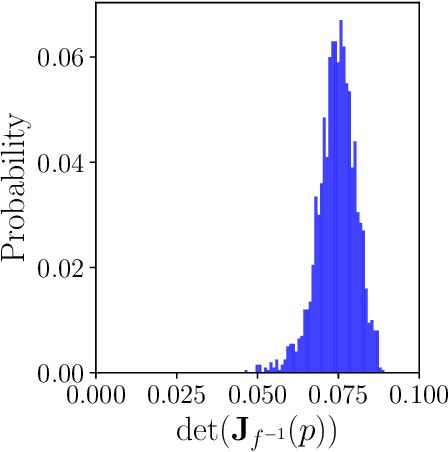
Parameter identifiability refers to the capability of accurately inferring the parameter values of a model from its observations (data). Traditional analysis methods exploit analytical properties of the closed form model, in particular sensitivity analysis, to quantify the response of the model predictions to variations in parameters. Techniques developed to analyze data, specifically manifold learning methods, have the potential to complement, and even extend the scope of the traditional analytical approaches. We report on a study comparing and contrasting analytical and data-driven approaches to quantify parameter identifiability and, importantly, perform parameter reduction tasks. We use the infinite bus synchronous generator model, a well-understood model from the power systems domain, as our benchmark problem. Our traditional analysis methods use the Fisher Information Matrix to quantify parameter identifiability analysis, and the Manifold Boundary Approximation Method to perform parameter reduction. We compare these results to those arrived at through data-driven manifold learning schemes: Output - Diffusion Maps and Geometric Harmonics. For our test case, we find that the two suites of tools (analytical when a model is explicitly available, as well as data-driven when the model is lacking and only measurement data are available) give (correct) comparable results; these results are also in agreement with traditional analysis based on singular perturbation theory. We then discuss the prospects of using data-driven methods for such model analysis.

A Resolution Independent Neural Operator

The Deep operator network (DeepONet) is a powerful yet simple neural operator architecture that utilizes two deep neural networks to learn mappings between infinite-dimensional function spaces. This architecture is highly flexible, allowing the evaluation of the solution field at any location within the desired domain. However, it imposes a strict constraint on the input space, requiring all input functions to be discretized at the same locations; this limits its practical applications. In this work, we introduce a Resolution Independent Neural Operator (RINO) that provides a framework to make DeepONet resolution-independent, enabling it to handle input functions that are arbitrarily, but sufficiently finely, discretized. To this end, we propose a dictionary learning algorithm to adaptively learn a set of appropriate continuous basis functions, parameterized as implicit neural representations (INRs), from the input data. These basis functions are then used to project arbitrary input function data as a point cloud onto an embedding space (i.e., a vector space of finite dimensions) with dimensionality equal to the dictionary size, which can be directly used by DeepONet without any architectural changes. In particular, we utilize sinusoidal representation networks (SIRENs) as our trainable INR basis functions. We demonstrate the robustness and applicability of RINO in handling arbitrarily (but sufficiently richly) sampled input functions during both training and inference through several numerical examples.

Active search for Bifurcations

Bifurcations mark qualitative changes of long-term behavior in dynamical systems and can often signal sudden ("hard") transitions or catastrophic events (divergences). Accurately locating them is critical not just for deeper understanding of observed dynamic behavior, but also for designing efficient interventions. When the dynamical system at hand is complex, possibly noisy, and expensive to sample, standard (e.g. continuation based) numerical methods may become impractical. We propose an active learning framework, where Bayesian Optimization is leveraged to discover saddle-node or Hopf bifurcations, from a judiciously chosen small number of vector field observations. Such an approach becomes especially attractive in systems whose state x parameter space exploration is resource-limited. It also naturally provides a framework for uncertainty quantification (aleatoric and epistemic), useful in systems with inherent stochasticity.

On Learning what to Learn: heterogeneous observations of dynamics and establishing (possibly causal) relations among them

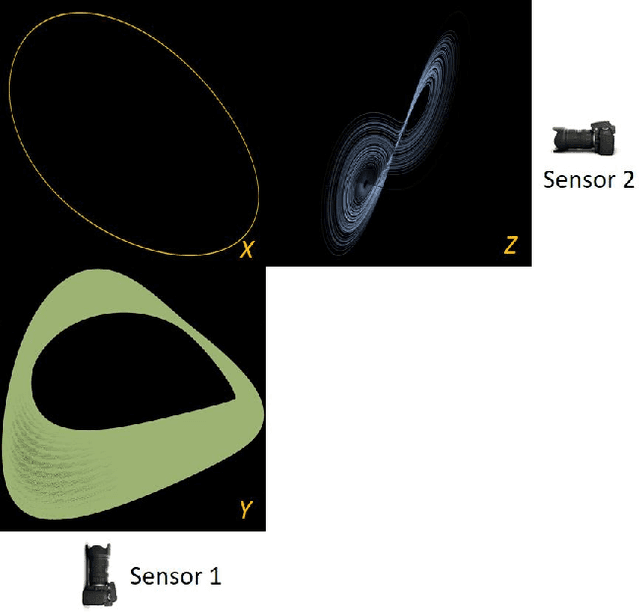
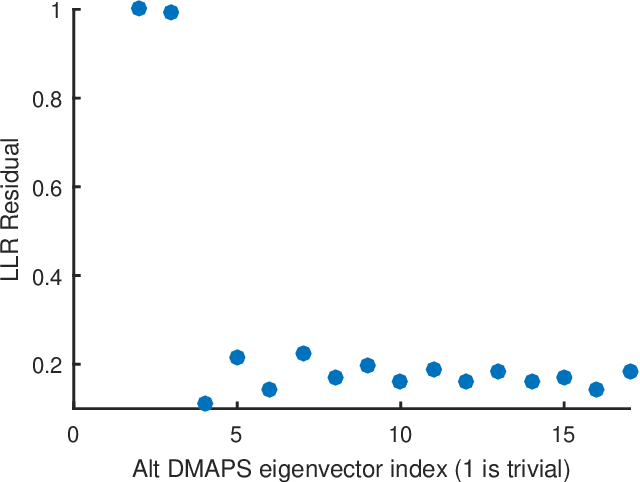
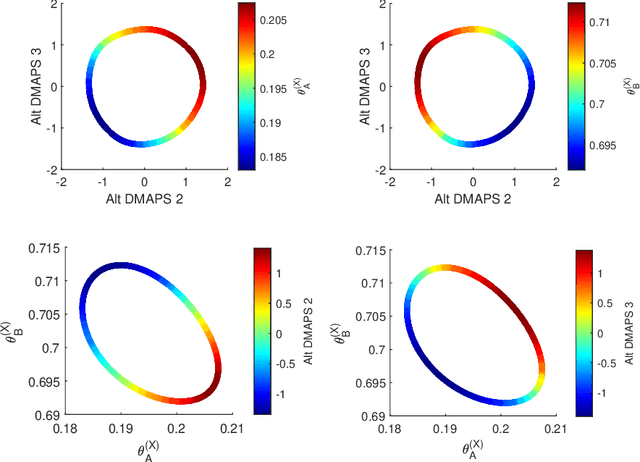
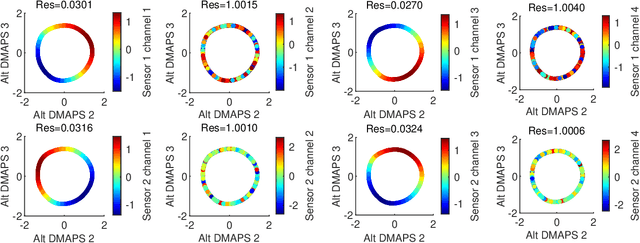
Before we attempt to learn a function between two (sets of) observables of a physical process, we must first decide what the inputs and what the outputs of the desired function are going to be. Here we demonstrate two distinct, data-driven ways of initially deciding ``the right quantities'' to relate through such a function, and then proceed to learn it. This is accomplished by processing multiple simultaneous heterogeneous data streams (ensembles of time series) from observations of a physical system: multiple observation processes of the system. We thus determine (a) what subsets of observables are common between the observation processes (and therefore observable from each other, relatable through a function); and (b) what information is unrelated to these common observables, and therefore particular to each observation process, and not contributing to the desired function. Any data-driven function approximation technique can subsequently be used to learn the input-output relation, from k-nearest neighbors and Geometric Harmonics to Gaussian Processes and Neural Networks. Two particular ``twists'' of the approach are discussed. The first has to do with the identifiability of particular quantities of interest from the measurements. We now construct mappings from a single set of observations of one process to entire level sets of measurements of the process, consistent with this single set. The second attempts to relate our framework to a form of causality: if one of the observation processes measures ``now'', while the second observation process measures ``in the future'', the function to be learned among what is common across observation processes constitutes a dynamical model for the system evolution.

RandONet: Shallow-Networks with Random Projections for learning linear and nonlinear operators

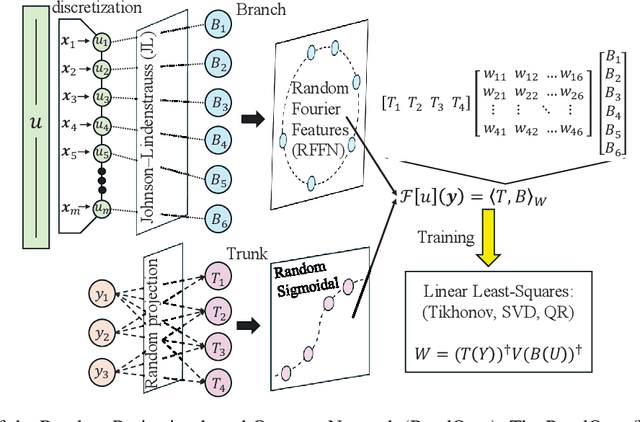
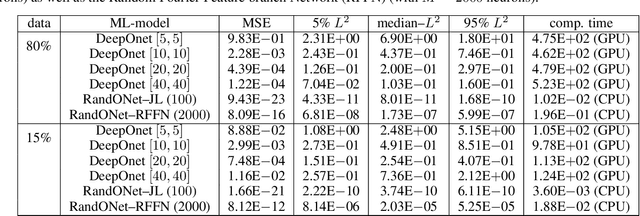
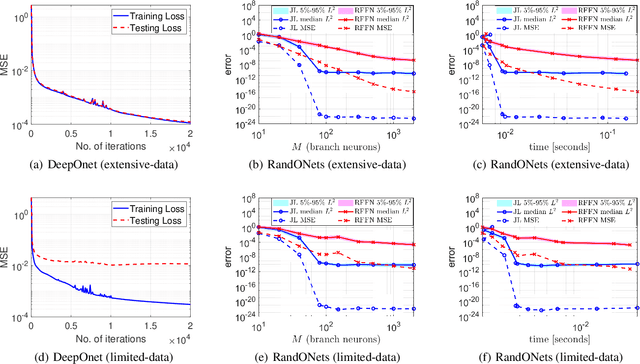
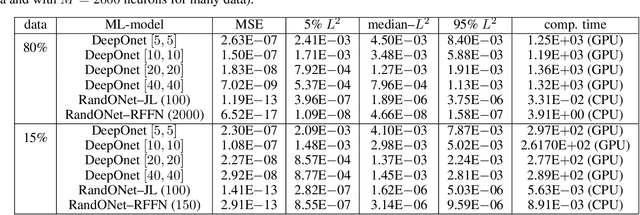
Deep Operator Networks (DeepOnets) have revolutionized the domain of scientific machine learning for the solution of the inverse problem for dynamical systems. However, their implementation necessitates optimizing a high-dimensional space of parameters and hyperparameters. This fact, along with the requirement of substantial computational resources, poses a barrier to achieving high numerical accuracy. Here, inpsired by DeepONets and to address the above challenges, we present Random Projection-based Operator Networks (RandONets): shallow networks with random projections that learn linear and nonlinear operators. The implementation of RandONets involves: (a) incorporating random bases, thus enabling the use of shallow neural networks with a single hidden layer, where the only unknowns are the output weights of the network's weighted inner product; this reduces dramatically the dimensionality of the parameter space; and, based on this, (b) using established least-squares solvers (e.g., Tikhonov regularization and preconditioned QR decomposition) that offer superior numerical approximation properties compared to other optimization techniques used in deep-learning. In this work, we prove the universal approximation accuracy of RandONets for approximating nonlinear operators and demonstrate their efficiency in approximating linear nonlinear evolution operators (right-hand-sides (RHS)) with a focus on PDEs. We show, that for this particular task, RandONets outperform, both in terms of numerical approximation accuracy and computational cost, the ``vanilla" DeepOnets.