Contrastive and Multi-Task Learning on Noisy Brain Signals with Nonlinear Dynamical Signatures

We introduce a two-stage multitask learning framework for analyzing Electroencephalography (EEG) signals that integrates denoising, dynamical modeling, and representation learning. In the first stage, a denoising autoencoder is trained to suppress artifacts and stabilize temporal dynamics, providing robust signal representations. In the second stage, a multitask architecture processes these denoised signals to achieve three objectives: motor imagery classification, chaotic versus non-chaotic regime discrimination using Lyapunov exponent-based labels, and self-supervised contrastive representation learning with NT-Xent loss. A convolutional backbone combined with a Transformer encoder captures spatial-temporal structure, while the dynamical task encourages sensitivity to nonlinear brain dynamics. This staged design mitigates interference between reconstruction and discriminative goals, improves stability across datasets, and supports reproducible training by clearly separating noise reduction from higher-level feature learning. Empirical studies show that our framework not only enhances robustness and generalization but also surpasses strong baselines and recent state-of-the-art methods in EEG decoding, highlighting the effectiveness of combining denoising, dynamical features, and self-supervised learning.

Rapid training of Hamiltonian graph networks without gradient descent

Learning dynamical systems that respect physical symmetries and constraints remains a fundamental challenge in data-driven modeling. Integrating physical laws with graph neural networks facilitates principled modeling of complex N-body dynamics and yields accurate and permutation-invariant models. However, training graph neural networks with iterative, gradient-based optimization algorithms (e.g., Adam, RMSProp, LBFGS) often leads to slow training, especially for large, complex systems. In comparison to 15 different optimizers, we demonstrate that Hamiltonian Graph Networks (HGN) can be trained up to 600x faster--but with comparable accuracy--by replacing iterative optimization with random feature-based parameter construction. We show robust performance in diverse simulations, including N-body mass-spring systems in up to 3 dimensions with different geometries, while retaining essential physical invariances with respect to permutation, rotation, and translation. We reveal that even when trained on minimal 8-node systems, the model can generalize in a zero-shot manner to systems as large as 4096 nodes without retraining. Our work challenges the dominance of iterative gradient-descent-based optimization algorithms for training neural network models for physical systems.

A Mesh Is Worth 512 Numbers: Spectral-domain Diffusion Modeling for High-dimension Shape Generation

Recent advancements in learning latent codes derived from high-dimensional shapes have demonstrated impressive outcomes in 3D generative modeling. Traditionally, these approaches employ a trained autoencoder to acquire a continuous implicit representation of source shapes, which can be computationally expensive. This paper introduces a novel framework, spectral-domain diffusion for high-quality shape generation SpoDify, that utilizes singular value decomposition (SVD) for shape encoding. The resulting eigenvectors can be stored for subsequent decoding, while generative modeling is performed on the eigenfeatures. This approach efficiently encodes complex meshes into continuous implicit representations, such as encoding a 15k-vertex mesh to a 512-dimensional latent code without learning. Our method exhibits significant advantages in scenarios with limited samples or GPU resources. In mesh generation tasks, our approach produces high-quality shapes that are comparable to state-of-the-art methods.

Training Hamiltonian neural networks without backpropagation

Neural networks that synergistically integrate data and physical laws offer great promise in modeling dynamical systems. However, iterative gradient-based optimization of network parameters is often computationally expensive and suffers from slow convergence. In this work, we present a backpropagation-free algorithm to accelerate the training of neural networks for approximating Hamiltonian systems through data-agnostic and data-driven algorithms. We empirically show that data-driven sampling of the network parameters outperforms data-agnostic sampling or the traditional gradient-based iterative optimization of the network parameters when approximating functions with steep gradients or wide input domains. We demonstrate that our approach is more than 100 times faster with CPUs than the traditionally trained Hamiltonian Neural Networks using gradient-based iterative optimization and is more than four orders of magnitude accurate in chaotic examples, including the H\'enon-Heiles system.

Gradient-free training of recurrent neural networks

Recurrent neural networks are a successful neural architecture for many time-dependent problems, including time series analysis, forecasting, and modeling of dynamical systems. Training such networks with backpropagation through time is a notoriously difficult problem because their loss gradients tend to explode or vanish. In this contribution, we introduce a computational approach to construct all weights and biases of a recurrent neural network without using gradient-based methods. The approach is based on a combination of random feature networks and Koopman operator theory for dynamical systems. The hidden parameters of a single recurrent block are sampled at random, while the outer weights are constructed using extended dynamic mode decomposition. This approach alleviates all problems with backpropagation commonly related to recurrent networks. The connection to Koopman operator theory also allows us to start using results in this area to analyze recurrent neural networks. In computational experiments on time series, forecasting for chaotic dynamical systems, and control problems, as well as on weather data, we observe that the training time and forecasting accuracy of the recurrent neural networks we construct are improved when compared to commonly used gradient-based methods.

Accelerating Full Waveform Inversion By Transfer Learning

Full waveform inversion (FWI) is a powerful tool for reconstructing material fields based on sparsely measured data obtained by wave propagation. For specific problems, discretizing the material field with a neural network (NN) improves the robustness and reconstruction quality of the corresponding optimization problem. We call this method NN-based FWI. Starting from an initial guess, the weights of the NN are iteratively updated to fit the simulated wave signals to the sparsely measured data set. For gradient-based optimization, a suitable choice of the initial guess, i.e., a suitable NN weight initialization, is crucial for fast and robust convergence. In this paper, we introduce a novel transfer learning approach to further improve NN-based FWI. This approach leverages supervised pretraining to provide a better NN weight initialization, leading to faster convergence of the subsequent optimization problem. Moreover, the inversions yield physically more meaningful local minima. The network is pretrained to predict the unknown material field using the gradient information from the first iteration of conventional FWI. In our computational experiments on two-dimensional domains, the training data set consists of reference simulations with arbitrarily positioned elliptical voids of different shapes and orientations. We compare the performance of the proposed transfer learning NN-based FWI with three other methods: conventional FWI, NN-based FWI without pretraining and conventional FWI with an initial guess predicted from the pretrained NN. Our results show that transfer learning NN-based FWI outperforms the other methods in terms of convergence speed and reconstruction quality.

On Learning what to Learn: heterogeneous observations of dynamics and establishing (possibly causal) relations among them

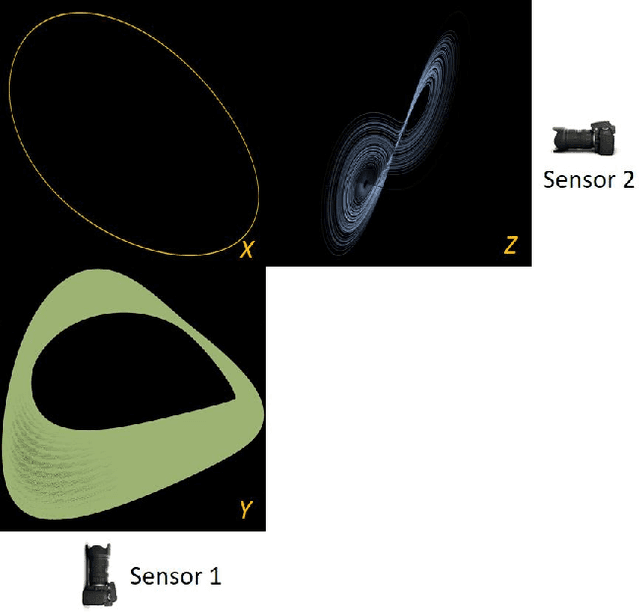
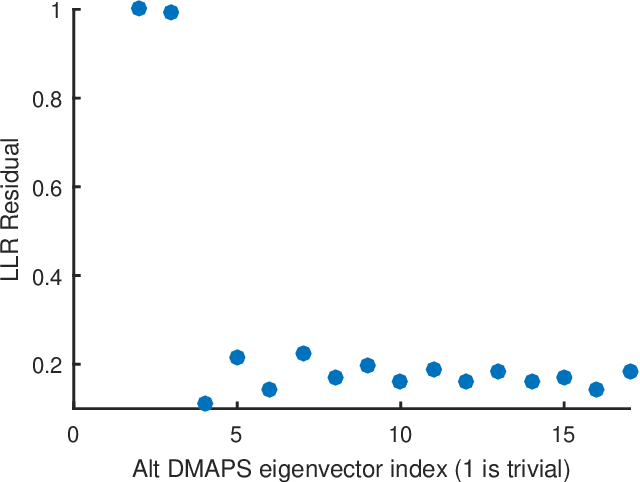
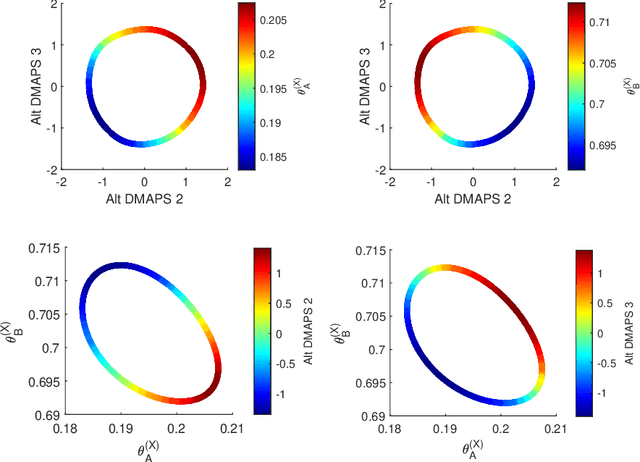
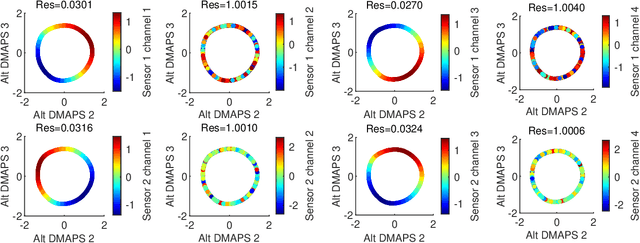
Before we attempt to learn a function between two (sets of) observables of a physical process, we must first decide what the inputs and what the outputs of the desired function are going to be. Here we demonstrate two distinct, data-driven ways of initially deciding ``the right quantities'' to relate through such a function, and then proceed to learn it. This is accomplished by processing multiple simultaneous heterogeneous data streams (ensembles of time series) from observations of a physical system: multiple observation processes of the system. We thus determine (a) what subsets of observables are common between the observation processes (and therefore observable from each other, relatable through a function); and (b) what information is unrelated to these common observables, and therefore particular to each observation process, and not contributing to the desired function. Any data-driven function approximation technique can subsequently be used to learn the input-output relation, from k-nearest neighbors and Geometric Harmonics to Gaussian Processes and Neural Networks. Two particular ``twists'' of the approach are discussed. The first has to do with the identifiability of particular quantities of interest from the measurements. We now construct mappings from a single set of observations of one process to entire level sets of measurements of the process, consistent with this single set. The second attempts to relate our framework to a form of causality: if one of the observation processes measures ``now'', while the second observation process measures ``in the future'', the function to be learned among what is common across observation processes constitutes a dynamical model for the system evolution.

Multi-fidelity Gaussian process surrogate modeling for regression problems in physics

One of the main challenges in surrogate modeling is the limited availability of data due to resource constraints associated with computationally expensive simulations. Multi-fidelity methods provide a solution by chaining models in a hierarchy with increasing fidelity, associated with lower error, but increasing cost. In this paper, we compare different multi-fidelity methods employed in constructing Gaussian process surrogates for regression. Non-linear autoregressive methods in the existing literature are primarily confined to two-fidelity models, and we extend these methods to handle more than two levels of fidelity. Additionally, we propose enhancements for an existing method incorporating delay terms by introducing a structured kernel. We demonstrate the performance of these methods across various academic and real-world scenarios. Our findings reveal that multi-fidelity methods generally have a smaller prediction error for the same computational cost as compared to the single-fidelity method, although their effectiveness varies across different scenarios.

Systematic construction of continuous-time neural networks for linear dynamical systems

Discovering a suitable neural network architecture for modeling complex dynamical systems poses a formidable challenge, often involving extensive trial and error and navigation through a high-dimensional hyper-parameter space. In this paper, we discuss a systematic approach to constructing neural architectures for modeling a subclass of dynamical systems, namely, Linear Time-Invariant (LTI) systems. We use a variant of continuous-time neural networks in which the output of each neuron evolves continuously as a solution of a first-order or second-order Ordinary Differential Equation (ODE). Instead of deriving the network architecture and parameters from data, we propose a gradient-free algorithm to compute sparse architecture and network parameters directly from the given LTI system, leveraging its properties. We bring forth a novel neural architecture paradigm featuring horizontal hidden layers and provide insights into why employing conventional neural architectures with vertical hidden layers may not be favorable. We also provide an upper bound on the numerical errors of our neural networks. Finally, we demonstrate the high accuracy of our constructed networks on three numerical examples.

Gappy local conformal auto-encoders for heterogeneous data fusion: in praise of rigidity

Fusing measurements from multiple, heterogeneous, partial sources, observing a common object or process, poses challenges due to the increasing availability of numbers and types of sensors. In this work we propose, implement and validate an end-to-end computational pipeline in the form of a multiple-auto-encoder neural network architecture for this task. The inputs to the pipeline are several sets of partial observations, and the result is a globally consistent latent space, harmonizing (rigidifying, fusing) all measurements. The key enabler is the availability of multiple slightly perturbed measurements of each instance:, local measurement, "bursts", that allows us to estimate the local distortion induced by each instrument. We demonstrate the approach in a sequence of examples, starting with simple two-dimensional data sets and proceeding to a Wi-Fi localization problem and to the solution of a "dynamical puzzle" arising in spatio-temporal observations of the solutions of Partial Differential Equations.