Multimodal Deep Learning for Dynamic and Static Neuroimaging: Integrating MRI and fMRI for Alzheimer Disease Analysis

Magnetic Resonance Imaging (MRI) provides detailed structural information, while functional MRI (fMRI) captures temporal brain activity. In this work, we present a multimodal deep learning framework that integrates MRI and fMRI for multi-class classification of Alzheimer Disease (AD), Mild Cognitive Impairment, and Normal Cognitive State. Structural features are extracted from MRI using 3D convolutional neural networks, while temporal features are learned from fMRI sequences using recurrent architectures. These representations are fused to enable joint spatial-temporal learning. Experiments were conducted on a small paired MRI-fMRI dataset (29 subjects), both with and without data augmentation. Results show that data augmentation substantially improves classification stability and generalization, particularly for the multimodal 3DCNN-LSTM model. In contrast, augmentation was found to be ineffective for a large-scale single-modality MRI dataset. These findings highlight the importance of dataset size and modality when designing augmentation strategies for neuroimaging-based AD classification.

Electrocardiogram Classification with Transformers Using Koopman and Wavelet Features

Electrocardiogram (ECG) analysis is vital for detecting cardiac abnormalities, yet robust automated classification is challenging due to the complexity and variability of physiological signals. In this work, we investigate transformer-based ECG classification using features derived from the Koopman operator and wavelet transforms. Two tasks are studied: (1) binary classification (Normal vs. Non-normal), and (2) four-class classification (Normal, Atrial Fibrillation, Ventricular Arrhythmia, Block). We use Extended Dynamic Mode Decomposition (EDMD) to approximate the Koopman operator. Our results show that wavelet features excel in binary classification, while Koopman features, when paired with transformers, achieve superior performance in the four-class setting. A simple hybrid of Koopman and wavelet features does not improve accuracy. However, selecting an appropriate EDMD dictionary -- specifically a radial basis function dictionary with tuned parameters -- yields significant gains, surpassing the wavelet-only baseline and the hybrid wavelet-Koopman system. We also present a Koopman-based reconstruction analysis for interpretable insights into the learned dynamics and compare against a recurrent neural network baseline. Overall, our findings demonstrate the effectiveness of Koopman-based feature learning with transformers and highlight promising directions for integrating dynamical systems theory into time-series classification.

Contrastive and Multi-Task Learning on Noisy Brain Signals with Nonlinear Dynamical Signatures

We introduce a two-stage multitask learning framework for analyzing Electroencephalography (EEG) signals that integrates denoising, dynamical modeling, and representation learning. In the first stage, a denoising autoencoder is trained to suppress artifacts and stabilize temporal dynamics, providing robust signal representations. In the second stage, a multitask architecture processes these denoised signals to achieve three objectives: motor imagery classification, chaotic versus non-chaotic regime discrimination using Lyapunov exponent-based labels, and self-supervised contrastive representation learning with NT-Xent loss. A convolutional backbone combined with a Transformer encoder captures spatial-temporal structure, while the dynamical task encourages sensitivity to nonlinear brain dynamics. This staged design mitigates interference between reconstruction and discriminative goals, improves stability across datasets, and supports reproducible training by clearly separating noise reduction from higher-level feature learning. Empirical studies show that our framework not only enhances robustness and generalization but also surpasses strong baselines and recent state-of-the-art methods in EEG decoding, highlighting the effectiveness of combining denoising, dynamical features, and self-supervised learning.

Gradient-free training of recurrent neural networks

Recurrent neural networks are a successful neural architecture for many time-dependent problems, including time series analysis, forecasting, and modeling of dynamical systems. Training such networks with backpropagation through time is a notoriously difficult problem because their loss gradients tend to explode or vanish. In this contribution, we introduce a computational approach to construct all weights and biases of a recurrent neural network without using gradient-based methods. The approach is based on a combination of random feature networks and Koopman operator theory for dynamical systems. The hidden parameters of a single recurrent block are sampled at random, while the outer weights are constructed using extended dynamic mode decomposition. This approach alleviates all problems with backpropagation commonly related to recurrent networks. The connection to Koopman operator theory also allows us to start using results in this area to analyze recurrent neural networks. In computational experiments on time series, forecasting for chaotic dynamical systems, and control problems, as well as on weather data, we observe that the training time and forecasting accuracy of the recurrent neural networks we construct are improved when compared to commonly used gradient-based methods.

Almost-Linear RNNs Yield Highly Interpretable Symbolic Codes in Dynamical Systems Reconstruction

Dynamical systems (DS) theory is fundamental for many areas of science and engineering. It can provide deep insights into the behavior of systems evolving in time, as typically described by differential or recursive equations. A common approach to facilitate mathematical tractability and interpretability of DS models involves decomposing nonlinear DS into multiple linear DS separated by switching manifolds, i.e. piecewise linear (PWL) systems. PWL models are popular in engineering and a frequent choice in mathematics for analyzing the topological properties of DS. However, hand-crafting such models is tedious and only possible for very low-dimensional scenarios, while inferring them from data usually gives rise to unnecessarily complex representations with very many linear subregions. Here we introduce Almost-Linear Recurrent Neural Networks (AL-RNNs) which automatically and robustly produce most parsimonious PWL representations of DS from time series data, using as few PWL nonlinearities as possible. AL-RNNs can be efficiently trained with any SOTA algorithm for dynamical systems reconstruction (DSR), and naturally give rise to a symbolic encoding of the underlying DS that provably preserves important topological properties. We show that for the Lorenz and R\"ossler systems, AL-RNNs discover, in a purely data-driven way, the known topologically minimal PWL representations of the corresponding chaotic attractors. We further illustrate on two challenging empirical datasets that interpretable symbolic encodings of the dynamics can be achieved, tremendously facilitating mathematical and computational analysis of the underlying systems.

Out-of-Domain Generalization in Dynamical Systems Reconstruction

In science we are interested in finding the governing equations, the dynamical rules, underlying empirical phenomena. While traditionally scientific models are derived through cycles of human insight and experimentation, recently deep learning (DL) techniques have been advanced to reconstruct dynamical systems (DS) directly from time series data. State-of-the-art dynamical systems reconstruction (DSR) methods show promise in capturing invariant and long-term properties of observed DS, but their ability to generalize to unobserved domains remains an open challenge. Yet, this is a crucial property we would expect from any viable scientific theory. In this work, we provide a formal framework that addresses generalization in DSR. We explain why and how out-of-domain (OOD) generalization (OODG) in DSR profoundly differs from OODG considered elsewhere in machine learning. We introduce mathematical notions based on topological concepts and ergodic theory to formalize the idea of learnability of a DSR model. We formally prove that black-box DL techniques, without adequate structural priors, generally will not be able to learn a generalizing DSR model. We also show this empirically, considering major classes of DSR algorithms proposed so far, and illustrate where and why they fail to generalize across the whole phase space. Our study provides the first comprehensive mathematical treatment of OODG in DSR, and gives a deeper conceptual understanding of where the fundamental problems in OODG lie and how they could possibly be addressed in practice.

Bifurcations and loss jumps in RNN training

Recurrent neural networks (RNNs) are popular machine learning tools for modeling and forecasting sequential data and for inferring dynamical systems (DS) from observed time series. Concepts from DS theory (DST) have variously been used to further our understanding of both, how trained RNNs solve complex tasks, and the training process itself. Bifurcations are particularly important phenomena in DS, including RNNs, that refer to topological (qualitative) changes in a system's dynamical behavior as one or more of its parameters are varied. Knowing the bifurcation structure of an RNN will thus allow to deduce many of its computational and dynamical properties, like its sensitivity to parameter variations or its behavior during training. In particular, bifurcations may account for sudden loss jumps observed in RNN training that could severely impede the training process. Here we first mathematically prove for a particular class of ReLU-based RNNs that certain bifurcations are indeed associated with loss gradients tending toward infinity or zero. We then introduce a novel heuristic algorithm for detecting all fixed points and k-cycles in ReLU-based RNNs and their existence and stability regions, hence bifurcation manifolds in parameter space. In contrast to previous numerical algorithms for finding fixed points and common continuation methods, our algorithm provides exact results and returns fixed points and cycles up to high orders with surprisingly good scaling behavior. We exemplify the algorithm on the analysis of the training process of RNNs, and find that the recently introduced technique of generalized teacher forcing completely avoids certain types of bifurcations in training. Thus, besides facilitating the DST analysis of trained RNNs, our algorithm provides a powerful instrument for analyzing the training process itself.

Generalized Teacher Forcing for Learning Chaotic Dynamics

Chaotic dynamical systems (DS) are ubiquitous in nature and society. Often we are interested in reconstructing such systems from observed time series for prediction or mechanistic insight, where by reconstruction we mean learning geometrical and invariant temporal properties of the system in question (like attractors). However, training reconstruction algorithms like recurrent neural networks (RNNs) on such systems by gradient-descent based techniques faces severe challenges. This is mainly due to exploding gradients caused by the exponential divergence of trajectories in chaotic systems. Moreover, for (scientific) interpretability we wish to have as low dimensional reconstructions as possible, preferably in a model which is mathematically tractable. Here we report that a surprisingly simple modification of teacher forcing leads to provably strictly all-time bounded gradients in training on chaotic systems, and, when paired with a simple architectural rearrangement of a tractable RNN design, piecewise-linear RNNs (PLRNNs), allows for faithful reconstruction in spaces of at most the dimensionality of the observed system. We show on several DS that with these amendments we can reconstruct DS better than current SOTA algorithms, in much lower dimensions. Performance differences were particularly compelling on real world data with which most other methods severely struggled. This work thus led to a simple yet powerful DS reconstruction algorithm which is highly interpretable at the same time.

Tractable Dendritic RNNs for Reconstructing Nonlinear Dynamical Systems

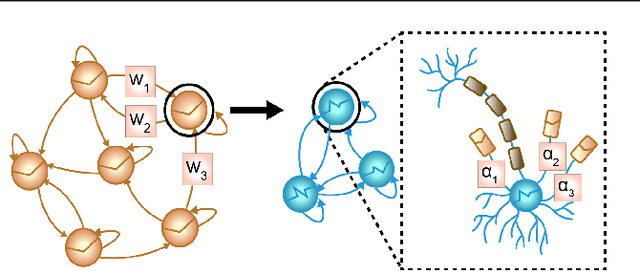
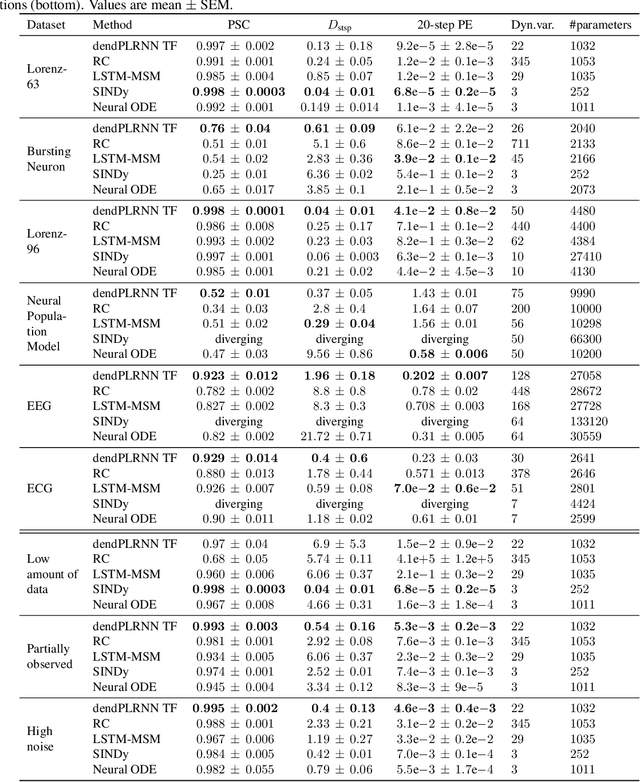
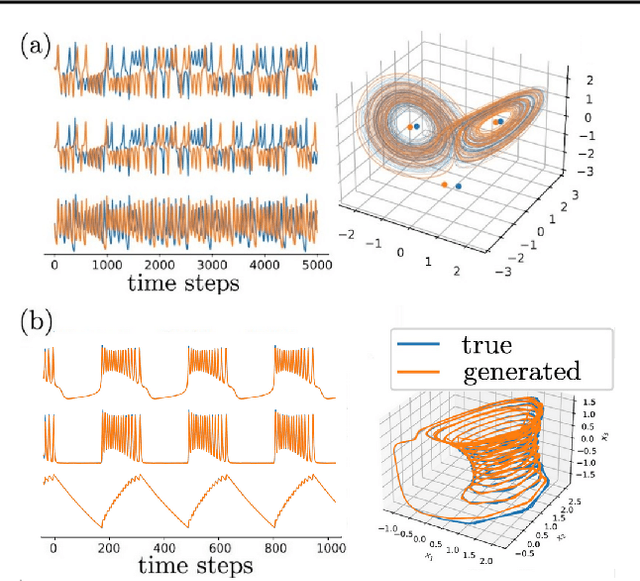
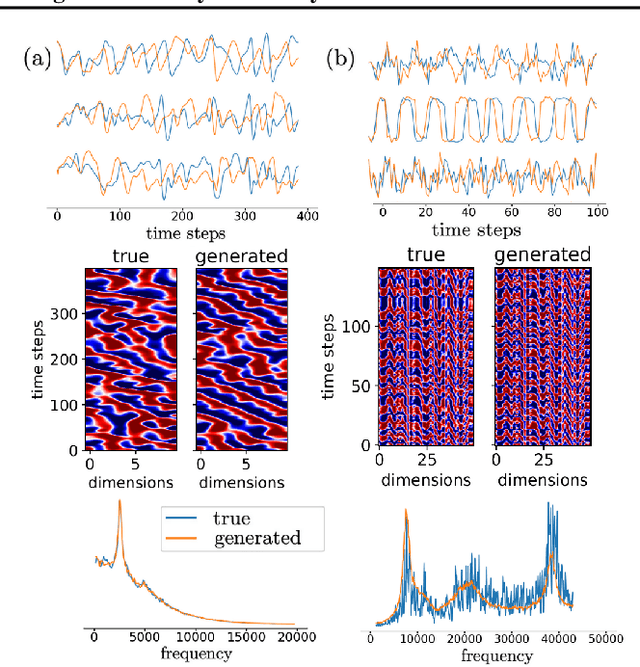
In many scientific disciplines, we are interested in inferring the nonlinear dynamical system underlying a set of observed time series, a challenging task in the face of chaotic behavior and noise. Previous deep learning approaches toward this goal often suffered from a lack of interpretability and tractability. In particular, the high-dimensional latent spaces often required for a faithful embedding, even when the underlying dynamics lives on a lower-dimensional manifold, can hamper theoretical analysis. Motivated by the emerging principles of dendritic computation, we augment a dynamically interpretable and mathematically tractable piecewise-linear (PL) recurrent neural network (RNN) by a linear spline basis expansion. We show that this approach retains all the theoretically appealing properties of the simple PLRNN, yet boosts its capacity for approximating arbitrary nonlinear dynamical systems in comparatively low dimensions. We employ two frameworks for training the system, one combining back-propagation-through-time (BPTT) with teacher forcing, and another based on fast and scalable variational inference. We show that the dendritically expanded PLRNN achieves better reconstructions with fewer parameters and dimensions on various dynamical systems benchmarks and compares favorably to other methods, while retaining a tractable and interpretable structure.

How to train RNNs on chaotic data?

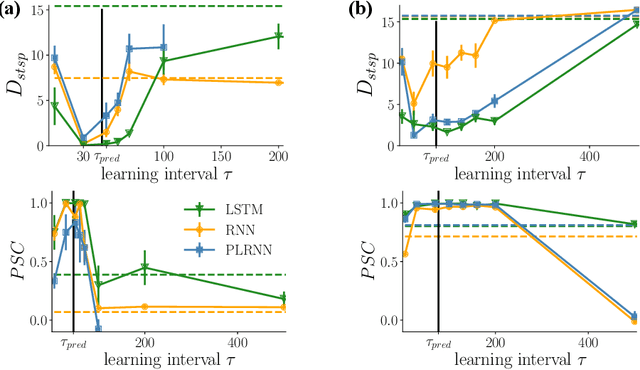
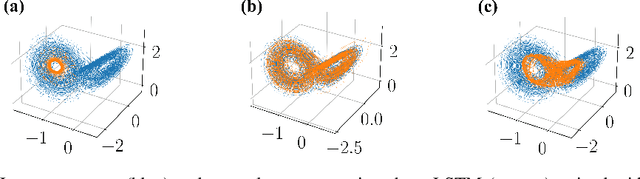
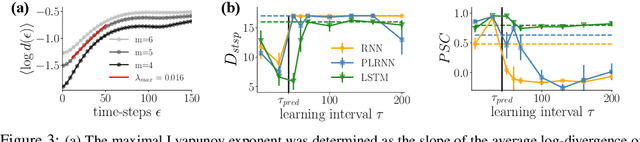
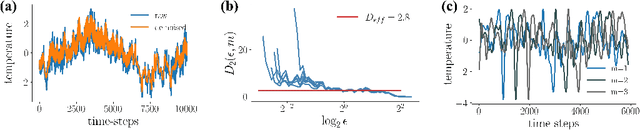
Recurrent neural networks (RNNs) are wide-spread machine learning tools for modeling sequential and time series data. They are notoriously hard to train because their loss gradients backpropagated in time tend to saturate or diverge during training. This is known as the exploding and vanishing gradient problem. Previous solutions to this issue either built on rather complicated, purpose-engineered architectures with gated memory buffers, or - more recently - imposed constraints that ensure convergence to a fixed point or restrict (the eigenspectrum of) the recurrence matrix. Such constraints, however, convey severe limitations on the expressivity of the RNN. Essential intrinsic dynamics such as multistability or chaos are disabled. This is inherently at disaccord with the chaotic nature of many, if not most, time series encountered in nature and society. Here we offer a comprehensive theoretical treatment of this problem by relating the loss gradients during RNN training to the Lyapunov spectrum of RNN-generated orbits. We mathematically prove that RNNs producing stable equilibrium or cyclic behavior have bounded gradients, whereas the gradients of RNNs with chaotic dynamics always diverge. Based on these analyses and insights, we offer an effective yet simple training technique for chaotic data and guidance on how to choose relevant hyperparameters according to the Lyapunov spectrum.