Tractable Dendritic RNNs for Reconstructing Nonlinear Dynamical Systems

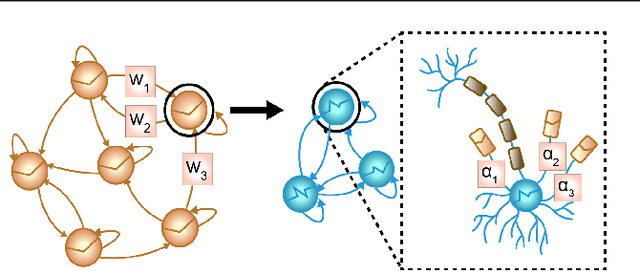
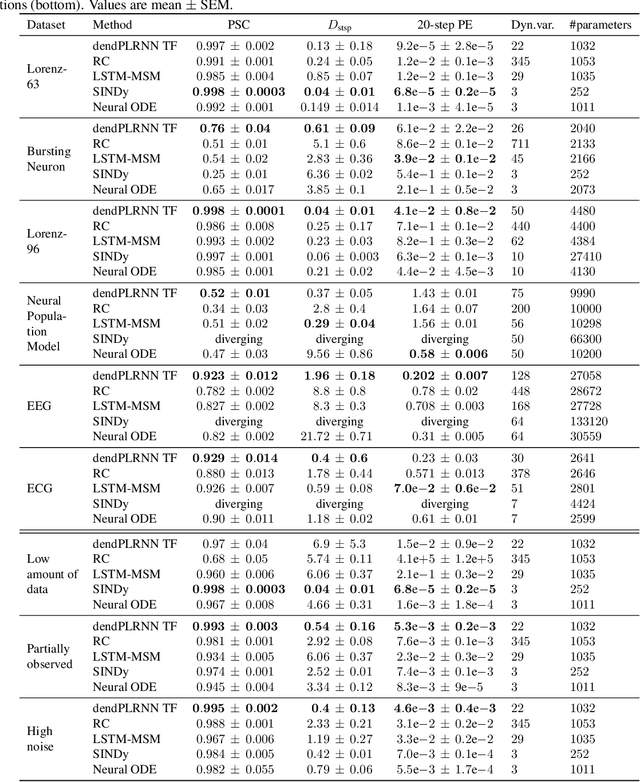
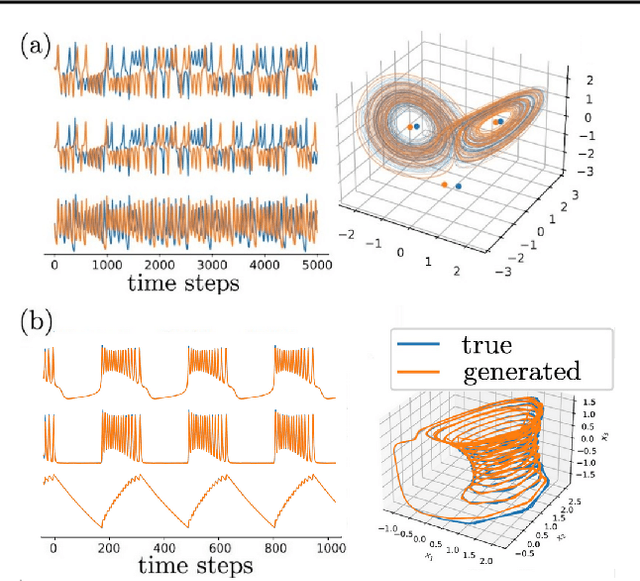
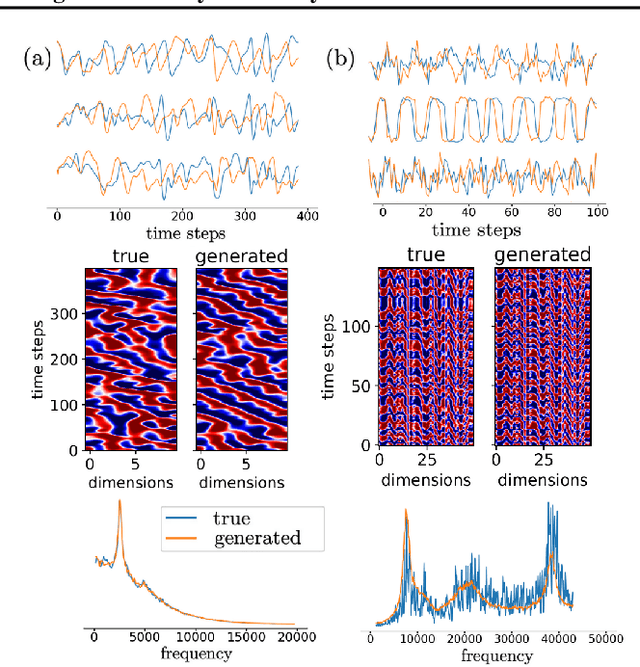
In many scientific disciplines, we are interested in inferring the nonlinear dynamical system underlying a set of observed time series, a challenging task in the face of chaotic behavior and noise. Previous deep learning approaches toward this goal often suffered from a lack of interpretability and tractability. In particular, the high-dimensional latent spaces often required for a faithful embedding, even when the underlying dynamics lives on a lower-dimensional manifold, can hamper theoretical analysis. Motivated by the emerging principles of dendritic computation, we augment a dynamically interpretable and mathematically tractable piecewise-linear (PL) recurrent neural network (RNN) by a linear spline basis expansion. We show that this approach retains all the theoretically appealing properties of the simple PLRNN, yet boosts its capacity for approximating arbitrary nonlinear dynamical systems in comparatively low dimensions. We employ two frameworks for training the system, one combining back-propagation-through-time (BPTT) with teacher forcing, and another based on fast and scalable variational inference. We show that the dendritically expanded PLRNN achieves better reconstructions with fewer parameters and dimensions on various dynamical systems benchmarks and compares favorably to other methods, while retaining a tractable and interpretable structure.

How to train RNNs on chaotic data?

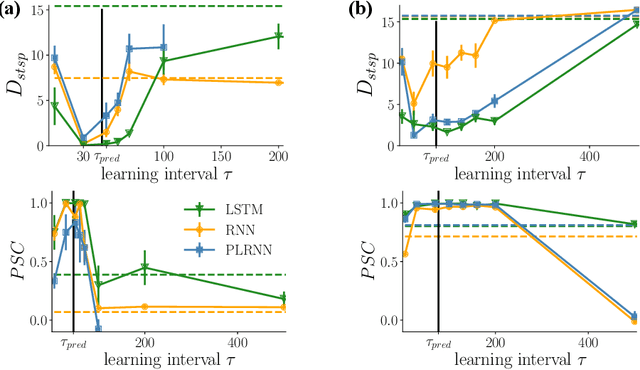
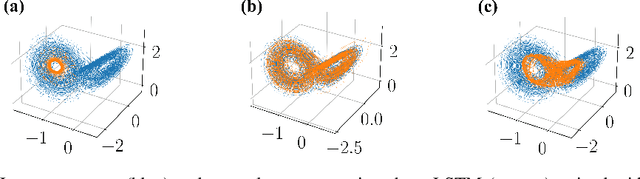
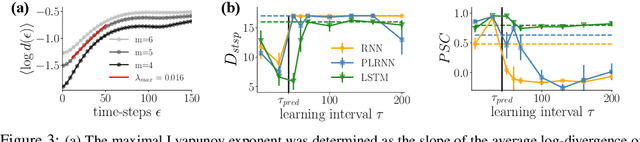
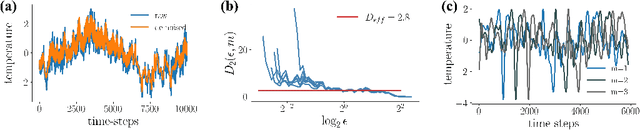
Recurrent neural networks (RNNs) are wide-spread machine learning tools for modeling sequential and time series data. They are notoriously hard to train because their loss gradients backpropagated in time tend to saturate or diverge during training. This is known as the exploding and vanishing gradient problem. Previous solutions to this issue either built on rather complicated, purpose-engineered architectures with gated memory buffers, or - more recently - imposed constraints that ensure convergence to a fixed point or restrict (the eigenspectrum of) the recurrence matrix. Such constraints, however, convey severe limitations on the expressivity of the RNN. Essential intrinsic dynamics such as multistability or chaos are disabled. This is inherently at disaccord with the chaotic nature of many, if not most, time series encountered in nature and society. Here we offer a comprehensive theoretical treatment of this problem by relating the loss gradients during RNN training to the Lyapunov spectrum of RNN-generated orbits. We mathematically prove that RNNs producing stable equilibrium or cyclic behavior have bounded gradients, whereas the gradients of RNNs with chaotic dynamics always diverge. Based on these analyses and insights, we offer an effective yet simple training technique for chaotic data and guidance on how to choose relevant hyperparameters according to the Lyapunov spectrum.