Implementing LLMs in industrial process modeling: Addressing Categorical Variables

Important variables of processes are, in many occasions, categorical, i.e. names or labels representing, e.g. categories of inputs, or types of reactors or a sequence of steps. In this work, we use Large Language Models (LLMs) to derive embeddings of such inputs that represent their actual meaning, or reflect the ``distances" between categories, i.e. how similar or dissimilar they are. This is a marked difference from the current standard practice of using binary, or one-hot encoding to replace categorical variables with sequences of ones and zeros. Combined with dimensionality reduction techniques, either linear such as Principal Components Analysis (PCA), or nonlinear such as Uniform Manifold Approximation and Projection (UMAP), the proposed approach leads to a \textit{meaningful}, low-dimensional feature space. The significance of obtaining meaningful embeddings is illustrated in the context of an industrial coating process for cutting tools that includes both numerical and categorical inputs. The proposed approach enables feature importance which is a marked improvement compared to the current state-of-the-art (SotA) in the encoding of categorical variables.

Conformal Disentanglement: A Neural Framework for Perspective Synthesis and Differentiation

For multiple scientific endeavors it is common to measure a phenomenon of interest in more than one ways. We make observations of objects from several different perspectives in space, at different points in time; we may also measure different properties of a mixture using different types of instruments. After collecting this heterogeneous information, it is necessary to be able to synthesize a complete picture of what is `common' across its sources: the subject we ultimately want to study. However, isolated (`clean') observations of a system are not always possible: observations often contain information about other systems in its environment, or about the measuring instruments themselves. In that sense, each observation may contain information that `does not matter' to the original object of study; this `uncommon' information between sensors observing the same object may still be important, and decoupling it from the main signal(s) useful. We introduce a neural network autoencoder framework capable of both tasks: it is structured to identify `common' variables, and, making use of orthogonality constraints to define geometric independence, to also identify disentangled `uncommon' information originating from the heterogeneous sensors. We demonstrate applications in several computational examples.

On Learning what to Learn: heterogeneous observations of dynamics and establishing (possibly causal) relations among them

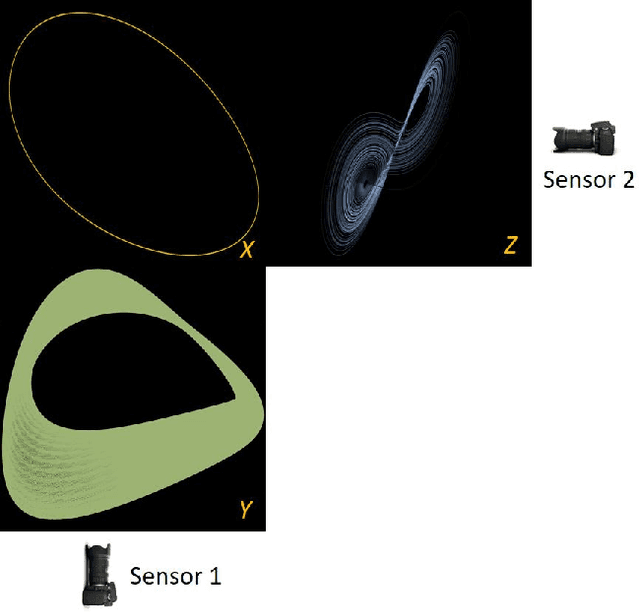
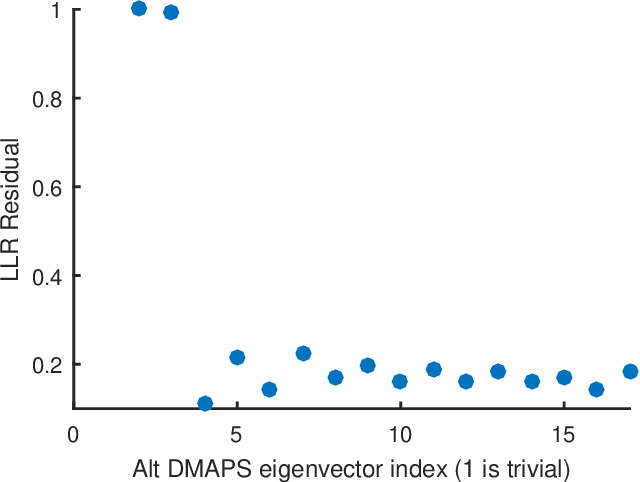
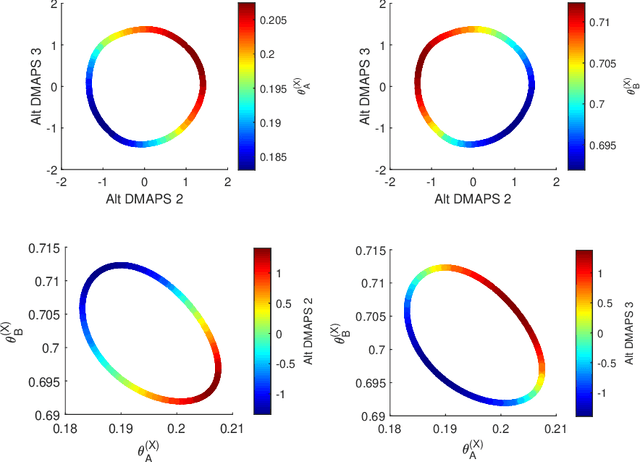
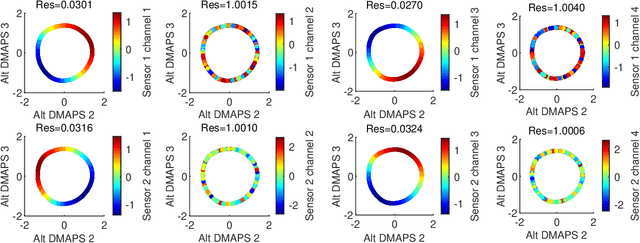
Before we attempt to learn a function between two (sets of) observables of a physical process, we must first decide what the inputs and what the outputs of the desired function are going to be. Here we demonstrate two distinct, data-driven ways of initially deciding ``the right quantities'' to relate through such a function, and then proceed to learn it. This is accomplished by processing multiple simultaneous heterogeneous data streams (ensembles of time series) from observations of a physical system: multiple observation processes of the system. We thus determine (a) what subsets of observables are common between the observation processes (and therefore observable from each other, relatable through a function); and (b) what information is unrelated to these common observables, and therefore particular to each observation process, and not contributing to the desired function. Any data-driven function approximation technique can subsequently be used to learn the input-output relation, from k-nearest neighbors and Geometric Harmonics to Gaussian Processes and Neural Networks. Two particular ``twists'' of the approach are discussed. The first has to do with the identifiability of particular quantities of interest from the measurements. We now construct mappings from a single set of observations of one process to entire level sets of measurements of the process, consistent with this single set. The second attempts to relate our framework to a form of causality: if one of the observation processes measures ``now'', while the second observation process measures ``in the future'', the function to be learned among what is common across observation processes constitutes a dynamical model for the system evolution.

Discovering deposition process regimes: leveraging unsupervised learning for process insights, surrogate modeling, and sensitivity analysis

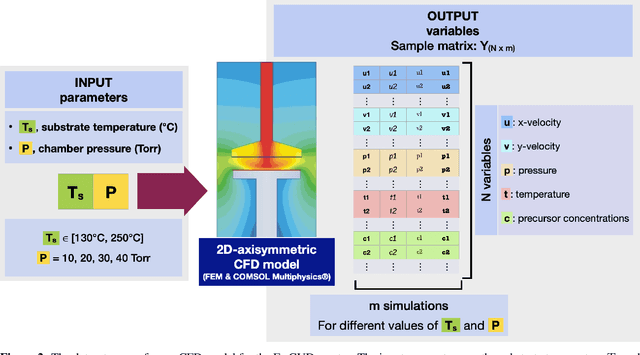
This work introduces a comprehensive approach utilizing data-driven methods to elucidate the deposition process regimes in Chemical Vapor Deposition (CVD) reactors and the interplay of physical mechanism that dominate in each one of them. Through this work, we address three key objectives. Firstly, our methodology relies on process outcomes, derived by a detailed CFD model, to identify clusters of "outcomes" corresponding to distinct process regimes, wherein the relative influence of input variables undergoes notable shifts. This phenomenon is experimentally validated through Arrhenius plot analysis, affirming the efficacy of our approach. Secondly, we demonstrate the development of an efficient surrogate model, based on Polynomial Chaos Expansion (PCE), that maintains accuracy, facilitating streamlined computational analyses. Finally, as a result of PCE, sensitivity analysis is made possible by means of Sobol' indices, that quantify the impact of process inputs across identified regimes. The insights gained from our analysis contribute to the formulation of hypotheses regarding phenomena occurring beyond the transition regime. Notably, the significance of temperature even in the diffusion-limited regime, as evidenced by the Arrhenius plot, suggests activation of gas phase reactions at elevated temperatures. Importantly, our proposed methods yield insights that align with experimental observations and theoretical principles, aiding decision-making in process design and optimization. By circumventing the need for costly and time-consuming experiments, our approach offers a pragmatic pathway towards enhanced process efficiency. Moreover, this study underscores the potential of data-driven computational methods for innovating reactor design paradigms.

Integrating supervised and unsupervised learning approaches to unveil critical process inputs

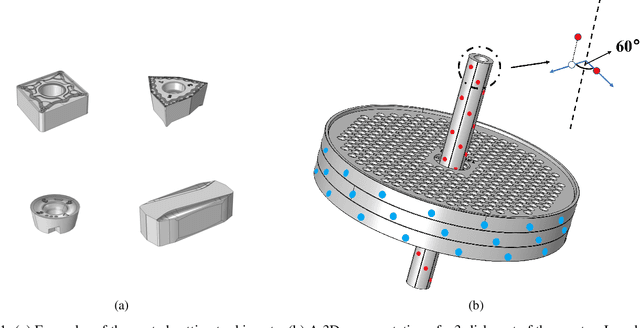
This study introduces a machine learning framework tailored to large-scale industrial processes characterized by a plethora of numerical and categorical inputs. The framework aims to (i) discern critical parameters influencing the output and (ii) generate accurate out-of-sample qualitative and quantitative predictions of production outcomes. Specifically, we address the pivotal question of the significance of each input in shaping the process outcome, using an industrial Chemical Vapor Deposition (CVD) process as an example. The initial objective involves merging subject matter expertise and clustering techniques exclusively on the process output, here, coating thickness measurements at various positions in the reactor. This approach identifies groups of production runs that share similar qualitative characteristics, such as film mean thickness and standard deviation. In particular, the differences of the outcomes represented by the different clusters can be attributed to differences in specific inputs, indicating that these inputs are critical for the production outcome. Leveraging this insight, we subsequently implement supervised classification and regression methods using the identified critical process inputs. The proposed methodology proves to be valuable in scenarios with a multitude of inputs and insufficient data for the direct application of deep learning techniques, providing meaningful insights into the underlying processes.

Nonlinear Manifold Learning Determines Microgel Size from Raman Spectroscopy

Polymer particle size constitutes a crucial characteristic of product quality in polymerization. Raman spectroscopy is an established and reliable process analytical technology for in-line concentration monitoring. Recent approaches and some theoretical considerations show a correlation between Raman signals and particle sizes but do not determine polymer size from Raman spectroscopic measurements accurately and reliably. With this in mind, we propose three alternative machine learning workflows to perform this task, all involving diffusion maps, a nonlinear manifold learning technique for dimensionality reduction: (i) directly from diffusion maps, (ii) alternating diffusion maps, and (iii) conformal autoencoder neural networks. We apply the workflows to a data set of Raman spectra with associated size measured via dynamic light scattering of 47 microgel (cross-linked polymer) samples in a diameter range of 208nm to 483 nm. The conformal autoencoders substantially outperform state-of-the-art methods and results for the first time in a promising prediction of polymer size from Raman spectra.

Nonlinear dimensionality reduction then and now: AIMs for dissipative PDEs in the ML era

This study presents a collection of purely data-driven workflows for constructing reduced-order models (ROMs) for distributed dynamical systems. The ROMs we focus on, are data-assisted models inspired by, and templated upon, the theory of Approximate Inertial Manifolds (AIMs); the particular motivation is the so-called post-processing Galerkin method of Garcia-Archilla, Novo and Titi. Its applicability can be extended: the need for accurate truncated Galerkin projections and for deriving closed-formed corrections can be circumvented using machine learning tools. When the right latent variables are not a priori known, we illustrate how autoencoders as well as Diffusion Maps (a manifold learning scheme) can be used to discover good sets of latent variables and test their explainability. The proposed methodology can express the ROMs in terms of (a) theoretical (Fourier coefficients), (b) linear data-driven (POD modes) and/or (c) nonlinear data-driven (Diffusion Maps) coordinates. Both Black-Box and (theoretically-informed and data-corrected) Gray-Box models are described; the necessity for the latter arises when truncated Galerkin projections are so inaccurate as to not be amenable to post-processing. We use the Chafee-Infante reaction-diffusion and the Kuramoto-Sivashinsky dissipative partial differential equations to illustrate and successfully test the overall framework.