Towards Coordinate- and Dimension-Agnostic Machine Learning for Partial Differential Equations

The machine learning methods for data-driven identification of partial differential equations (PDEs) are typically defined for a given number of spatial dimensions and a choice of coordinates the data have been collected in. This dependence prevents the learned evolution equation from generalizing to other spaces. In this work, we reformulate the problem in terms of coordinate- and dimension-independent representations, paving the way toward what we call ``spatially liberated" PDE learning. To this end, we employ a machine learning approach to predict the evolution of scalar field systems expressed in the formalism of exterior calculus, which is coordinate-free and immediately generalizes to arbitrary dimensions by construction. We demonstrate the performance of this approach in the FitzHugh-Nagumo and Barkley reaction-diffusion models, as well as the Patlak-Keller-Segel model informed by in-situ chemotactic bacteria observations. We provide extensive numerical experiments that demonstrate that our approach allows for seamless transitions across various spatial contexts. We show that the field dynamics learned in one space can be used to make accurate predictions in other spaces with different dimensions, coordinate systems, boundary conditions, and curvatures.

Data-Driven, ML-assisted Approaches to Problem Well-Posedness

Classically, to solve differential equation problems, it is necessary to specify sufficient initial and/or boundary conditions so as to allow the existence of a unique solution. Well-posedness of differential equation problems thus involves studying the existence and uniqueness of solutions, and their dependence to such pre-specified conditions. However, in part due to mathematical necessity, these conditions are usually specified "to arbitrary precision" only on (appropriate portions of) the boundary of the space-time domain. This does not mirror how data acquisition is performed in realistic situations, where one may observe entire "patches" of solution data at arbitrary space-time locations; alternatively one might have access to more than one solutions stemming from the same differential operator. In our short work, we demonstrate how standard tools from machine and manifold learning can be used to infer, in a data driven manner, certain well-posedness features of differential equation problems, for initial/boundary condition combinations under which rigorous existence/uniqueness theorems are not known. Our study naturally combines a data assimilation perspective with an operator-learning one.

Thinner Latent Spaces: Detecting dimension and imposing invariance through autoencoder gradient constraints

Conformal Autoencoders are a neural network architecture that imposes orthogonality conditions between the gradients of latent variables towards achieving disentangled representations of data. In this letter we show that orthogonality relations within the latent layer of the network can be leveraged to infer the intrinsic dimensionality of nonlinear manifold data sets (locally characterized by the dimension of their tangent space), while simultaneously computing encoding and decoding (embedding) maps. We outline the relevant theory relying on differential geometry, and describe the corresponding gradient-descent optimization algorithm. The method is applied to standard data sets and we highlight its applicability, advantages, and shortcomings. In addition, we demonstrate that the same computational technology can be used to build coordinate invariance to local group actions when defined only on a (reduced) submanifold of the embedding space.

Conformal Disentanglement: A Neural Framework for Perspective Synthesis and Differentiation

For multiple scientific endeavors it is common to measure a phenomenon of interest in more than one ways. We make observations of objects from several different perspectives in space, at different points in time; we may also measure different properties of a mixture using different types of instruments. After collecting this heterogeneous information, it is necessary to be able to synthesize a complete picture of what is `common' across its sources: the subject we ultimately want to study. However, isolated (`clean') observations of a system are not always possible: observations often contain information about other systems in its environment, or about the measuring instruments themselves. In that sense, each observation may contain information that `does not matter' to the original object of study; this `uncommon' information between sensors observing the same object may still be important, and decoupling it from the main signal(s) useful. We introduce a neural network autoencoder framework capable of both tasks: it is structured to identify `common' variables, and, making use of orthogonality constraints to define geometric independence, to also identify disentangled `uncommon' information originating from the heterogeneous sensors. We demonstrate applications in several computational examples.

Machine Learning for the identification of phase-transitions in interacting agent-based systems

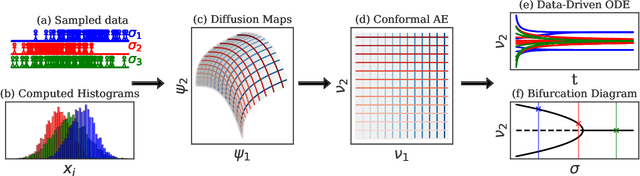
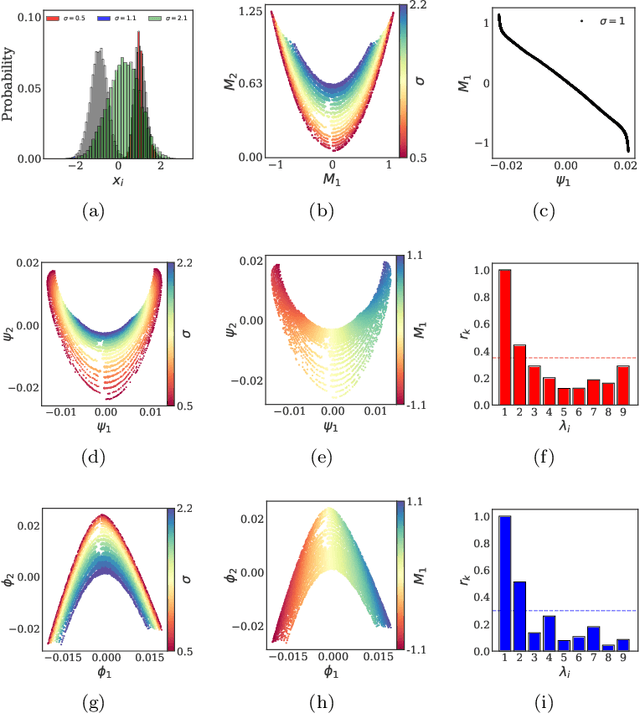
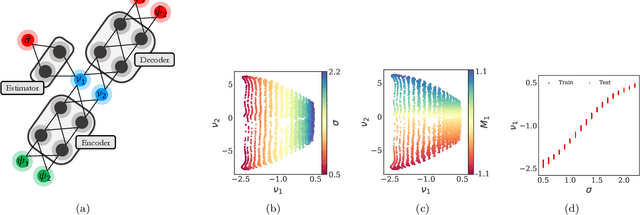
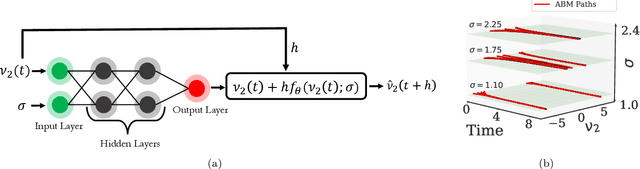
Deriving closed-form, analytical expressions for reduced-order models, and judiciously choosing the closures leading to them, has long been the strategy of choice for studying phase- and noise-induced transitions for agent-based models (ABMs). In this paper, we propose a data-driven framework that pinpoints phase transitions for an ABM in its mean-field limit, using a smaller number of variables than traditional closed-form models. To this end, we use the manifold learning algorithm Diffusion Maps to identify a parsimonious set of data-driven latent variables, and show that they are in one-to-one correspondence with the expected theoretical order parameter of the ABM. We then utilize a deep learning framework to obtain a conformal reparametrization of the data-driven coordinates that facilitates, in our example, the identification of a single parameter-dependent ODE in these coordinates. We identify this ODE through a residual neural network inspired by a numerical integration scheme (forward Euler). We then use the identified ODE -- enabled through an odd symmetry transformation -- to construct the bifurcation diagram exhibiting the phase transition.

The passive symmetries of machine learning

Any representation of data involves arbitrary investigator choices. Because those choices are external to the data-generating process, each choice leads to an exact symmetry, corresponding to the group of transformations that takes one possible representation to another. These are the passive symmetries; they include coordinate freedom, gauge symmetry and units covariance, all of which have led to important results in physics. Our goal is to understand the implications of passive symmetries for machine learning: Which passive symmetries play a role (e.g., permutation symmetry in graph neural networks)? What are dos and don'ts in machine learning practice? We assay conditions under which passive symmetries can be implemented as group equivariances. We also discuss links to causal modeling, and argue that the implementation of passive symmetries is particularly valuable when the goal of the learning problem is to generalize out of sample. While this paper is purely conceptual, we believe that it can have a significant impact on helping machine learning make the transition that took place for modern physics in the first half of the Twentieth century.

On the Parameter Combinations That Matter and on Those That do Not

We present a data-driven approach to characterizing nonidentifiability of a model's parameters and illustrate it through dynamic kinetic models. By employing Diffusion Maps and their extensions, we discover the minimal combinations of parameters required to characterize the dynamic output behavior: a set of effective parameters for the model. Furthermore, we use Conformal Autoencoder Neural Networks, as well as a kernel-based Jointly Smooth Function technique, to disentangle the redundant parameter combinations that do not affect the output behavior from the ones that do. We discuss the interpretability of our data-driven effective parameters and demonstrate the utility of the approach both for behavior prediction and parameter estimation. In the latter task, it becomes important to describe level sets in parameter space that are consistent with a particular output behavior. We validate our approach on a model of multisite phosphorylation, where a reduced set of effective parameters, nonlinear combinations of the physical ones, has previously been established analytically.