Diffeomorphic Latent Neural Operators for Data-Efficient Learning of Solutions to Partial Differential Equations

A computed approximation of the solution operator to a system of partial differential equations (PDEs) is needed in various areas of science and engineering. Neural operators have been shown to be quite effective at predicting these solution generators after training on high-fidelity ground truth data (e.g. numerical simulations). However, in order to generalize well to unseen spatial domains, neural operators must be trained on an extensive amount of geometrically varying data samples that may not be feasible to acquire or simulate in certain contexts (e.g., patient-specific medical data, large-scale computationally intensive simulations.) We propose that in order to learn a PDE solution operator that can generalize across multiple domains without needing to sample enough data expressive enough for all possible geometries, we can train instead a latent neural operator on just a few ground truth solution fields diffeomorphically mapped from different geometric/spatial domains to a fixed reference configuration. Furthermore, the form of the solutions is dependent on the choice of mapping to and from the reference domain. We emphasize that preserving properties of the differential operator when constructing these mappings can significantly reduce the data requirement for achieving an accurate model due to the regularity of the solution fields that the latent neural operator is training on. We provide motivating numerical experimentation that demonstrates an extreme case of this consideration by exploiting the conformal invariance of the Laplacian

Diffeomorphic Latent Neural Operator Learning for Data-Efficient Predictions of Solutions to Partial Differential Equations

A computed approximation of the solution operator to a system of partial differential equations (PDEs) is needed in various areas of science and engineering. Neural operators have been shown to be quite effective at predicting these solution generators after training on high-fidelity ground truth data (e.g. numerical simulations). However, in order to generalize well to unseen spatial domains, neural operators must be trained on an extensive amount of geometrically varying data samples that may not be feasible to acquire or simulate in certain contexts (i.e., patient-specific medical data, large-scale computationally intensive simulations.) We propose that in order to learn a PDE solution operator that can generalize across multiple domains without needing to sample enough data expressive enough for all possible geometries, we can train instead a latent neural operator on just a few ground truth solution fields diffeomorphically mapped from different geometric/spatial domains to a fixed reference configuration. Furthermore, the form of the solutions is dependent on the choice of mapping to and from the reference domain. We emphasize that preserving properties of the differential operator when constructing these mappings can significantly reduce the data requirement for achieving an accurate model due to the regularity of the solution fields that the latent neural operator is training on. We provide motivating numerical experimentation that demonstrates an extreme case of this consideration by exploiting the conformal invariance of the Laplacian

Conditional regression for the Nonlinear Single-Variable Model

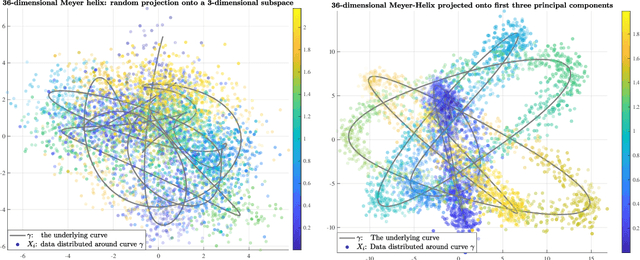
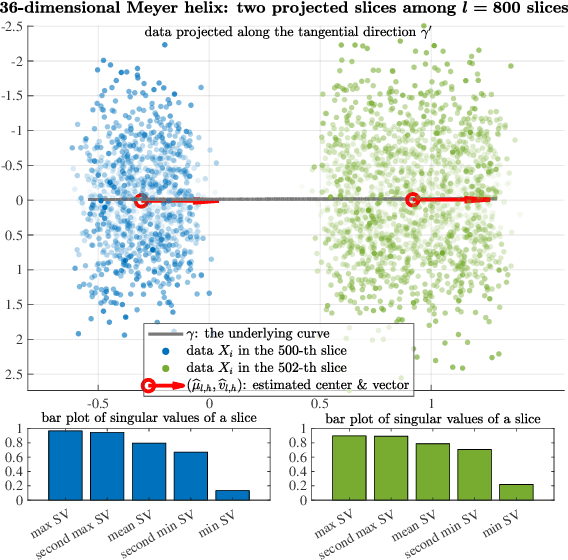
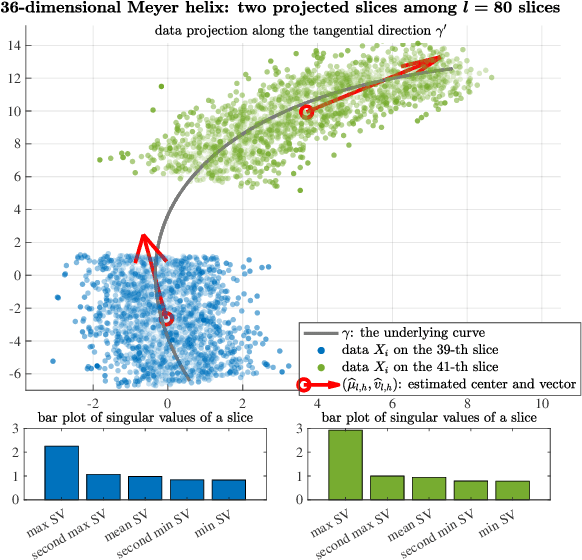
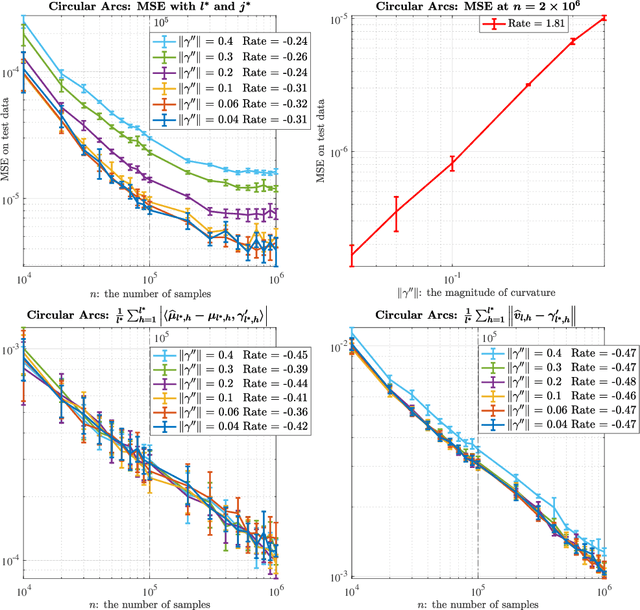
Several statistical models for regression of a function $F$ on $\mathbb{R}^d$ without the statistical and computational curse of dimensionality exist, for example by imposing and exploiting geometric assumptions on the distribution of the data (e.g. that its support is low-dimensional), or strong smoothness assumptions on $F$, or a special structure $F$. Among the latter, compositional models assume $F=f\circ g$ with $g$ mapping to $\mathbb{R}^r$ with $r\ll d$, have been studied, and include classical single- and multi-index models and recent works on neural networks. While the case where $g$ is linear is rather well-understood, much less is known when $g$ is nonlinear, and in particular for which $g$'s the curse of dimensionality in estimating $F$, or both $f$ and $g$, may be circumvented. In this paper, we consider a model $F(X):=f(\Pi_\gamma X) $ where $\Pi_\gamma:\mathbb{R}^d\to[0,\rm{len}_\gamma]$ is the closest-point projection onto the parameter of a regular curve $\gamma: [0,\rm{len}_\gamma]\to\mathbb{R}^d$ and $f:[0,\rm{len}_\gamma]\to\mathbb{R}^1$. The input data $X$ is not low-dimensional, far from $\gamma$, conditioned on $\Pi_\gamma(X)$ being well-defined. The distribution of the data, $\gamma$ and $f$ are unknown. This model is a natural nonlinear generalization of the single-index model, which corresponds to $\gamma$ being a line. We propose a nonparametric estimator, based on conditional regression, and show that under suitable assumptions, the strongest of which being that $f$ is coarsely monotone, it can achieve the $one$-$dimensional$ optimal min-max rate for non-parametric regression, up to the level of noise in the observations, and be constructed in time $\mathcal{O}(d^2n\log n)$. All the constants in the learning bounds, in the minimal number of samples required for our bounds to hold, and in the computational complexity are at most low-order polynomials in $d$.

Graph Fourier Neural Kernels (G-FuNK): Learning Solutions of Nonlinear Diffusive Parametric PDEs on Multiple Domains

Predicting time-dependent dynamics of complex systems governed by non-linear partial differential equations (PDEs) with varying parameters and domains is a challenging task motivated by applications across various fields. We introduce a novel family of neural operators based on our Graph Fourier Neural Kernels, designed to learn solution generators for nonlinear PDEs in which the highest-order term is diffusive, across multiple domains and parameters. G-FuNK combines components that are parameter- and domain-adapted with others that are not. The domain-adapted components are constructed using a weighted graph on the discretized domain, where the graph Laplacian approximates the highest-order diffusive term, ensuring boundary condition compliance and capturing the parameter and domain-specific behavior. Meanwhile, the learned components transfer across domains and parameters via Fourier Neural Operators. This approach naturally embeds geometric and directional information, improving generalization to new test domains without need for retraining the network. To handle temporal dynamics, our method incorporates an integrated ODE solver to predict the evolution of the system. Experiments show G-FuNK's capability to accurately approximate heat, reaction diffusion, and cardiac electrophysiology equations across various geometries and anisotropic diffusivity fields. G-FuNK achieves low relative errors on unseen domains and fiber fields, significantly accelerating predictions compared to traditional finite-element solvers.

Thinner Latent Spaces: Detecting dimension and imposing invariance through autoencoder gradient constraints

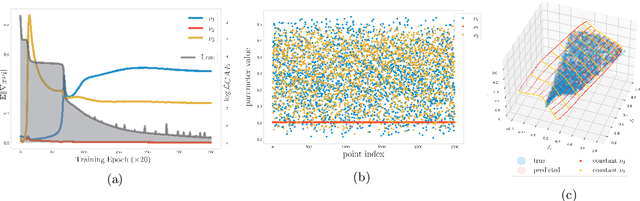
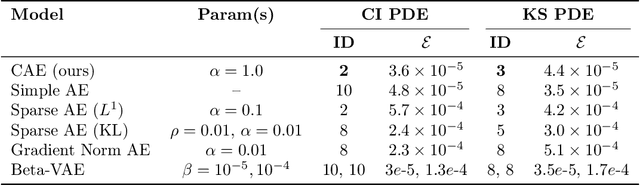
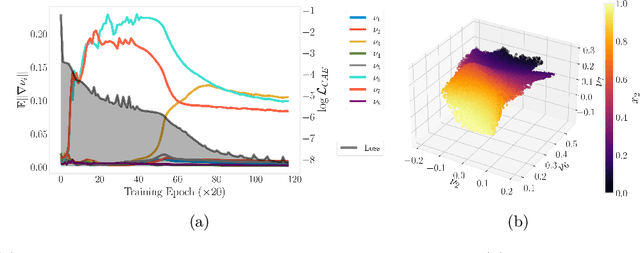
Conformal Autoencoders are a neural network architecture that imposes orthogonality conditions between the gradients of latent variables towards achieving disentangled representations of data. In this letter we show that orthogonality relations within the latent layer of the network can be leveraged to infer the intrinsic dimensionality of nonlinear manifold data sets (locally characterized by the dimension of their tangent space), while simultaneously computing encoding and decoding (embedding) maps. We outline the relevant theory relying on differential geometry, and describe the corresponding gradient-descent optimization algorithm. The method is applied to standard data sets and we highlight its applicability, advantages, and shortcomings. In addition, we demonstrate that the same computational technology can be used to build coordinate invariance to local group actions when defined only on a (reduced) submanifold of the embedding space.

Interacting Particle Systems on Networks: joint inference of the network and the interaction kernel

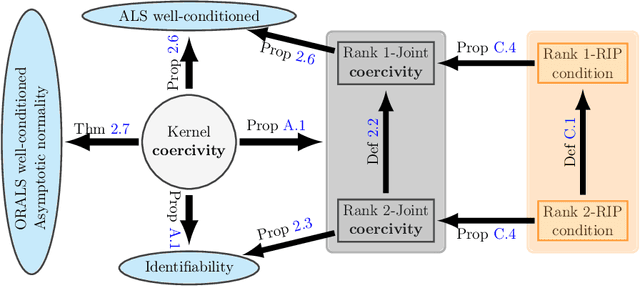
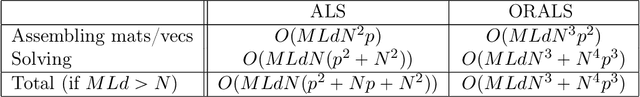
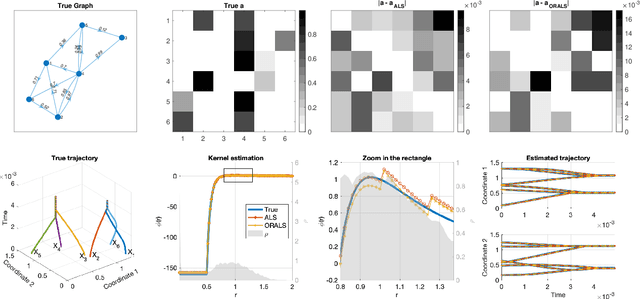
Modeling multi-agent systems on networks is a fundamental challenge in a wide variety of disciplines. We jointly infer the weight matrix of the network and the interaction kernel, which determine respectively which agents interact with which others and the rules of such interactions from data consisting of multiple trajectories. The estimator we propose leads naturally to a non-convex optimization problem, and we investigate two approaches for its solution: one is based on the alternating least squares (ALS) algorithm; another is based on a new algorithm named operator regression with alternating least squares (ORALS). Both algorithms are scalable to large ensembles of data trajectories. We establish coercivity conditions guaranteeing identifiability and well-posedness. The ALS algorithm appears statistically efficient and robust even in the small data regime but lacks performance and convergence guarantees. The ORALS estimator is consistent and asymptotically normal under a coercivity condition. We conduct several numerical experiments ranging from Kuramoto particle systems on networks to opinion dynamics in leader-follower models.

DIMON: Learning Solution Operators of Partial Differential Equations on a Diffeomorphic Family of Domains

The solution of a PDE over varying initial/boundary conditions on multiple domains is needed in a wide variety of applications, but it is computationally expensive if the solution is computed de novo whenever the initial/boundary conditions of the domain change. We introduce a general operator learning framework, called DIffeomorphic Mapping Operator learNing (DIMON) to learn approximate PDE solutions over a family of domains $\{\Omega_{\theta}}_\theta$, that learns the map from initial/boundary conditions and domain $\Omega_\theta$ to the solution of the PDE, or to specified functionals thereof. DIMON is based on transporting a given problem (initial/boundary conditions and domain $\Omega_{\theta}$) to a problem on a reference domain $\Omega_{0}$, where training data from multiple problems is used to learn the map to the solution on $\Omega_{0}$, which is then re-mapped to the original domain $\Omega_{\theta}$. We consider several problems to demonstrate the performance of the framework in learning both static and time-dependent PDEs on non-rigid geometries; these include solving the Laplace equation, reaction-diffusion equations, and a multiscale PDE that characterizes the electrical propagation on the left ventricle. This work paves the way toward the fast prediction of PDE solutions on a family of domains and the application of neural operators in engineering and precision medicine.

Learning Transition Operators From Sparse Space-Time Samples

We consider the nonlinear inverse problem of learning a transition operator $\mathbf{A}$ from partial observations at different times, in particular from sparse observations of entries of its powers $\mathbf{A},\mathbf{A}^2,\cdots,\mathbf{A}^{T}$. This Spatio-Temporal Transition Operator Recovery problem is motivated by the recent interest in learning time-varying graph signals that are driven by graph operators depending on the underlying graph topology. We address the nonlinearity of the problem by embedding it into a higher-dimensional space of suitable block-Hankel matrices, where it becomes a low-rank matrix completion problem, even if $\mathbf{A}$ is of full rank. For both a uniform and an adaptive random space-time sampling model, we quantify the recoverability of the transition operator via suitable measures of incoherence of these block-Hankel embedding matrices. For graph transition operators these measures of incoherence depend on the interplay between the dynamics and the graph topology. We develop a suitable non-convex iterative reweighted least squares (IRLS) algorithm, establish its quadratic local convergence, and show that, in optimal scenarios, no more than $\mathcal{O}(rn \log(nT))$ space-time samples are sufficient to ensure accurate recovery of a rank-$r$ operator $\mathbf{A}$ of size $n \times n$. This establishes that spatial samples can be substituted by a comparable number of space-time samples. We provide an efficient implementation of the proposed IRLS algorithm with space complexity of order $O(r n T)$ and per-iteration time complexity linear in $n$. Numerical experiments for transition operators based on several graph models confirm that the theoretical findings accurately track empirical phase transitions, and illustrate the applicability and scalability of the proposed algorithm.

Learning Interaction Variables and Kernels from Observations of Agent-Based Systems

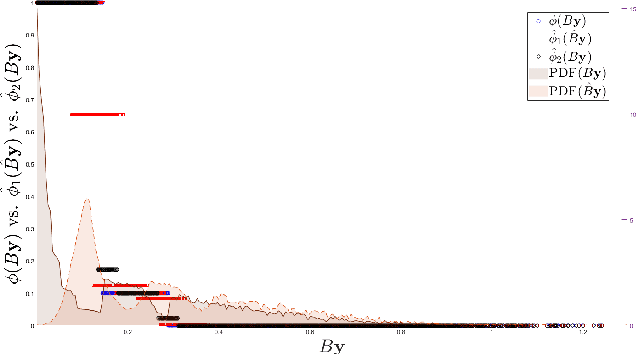
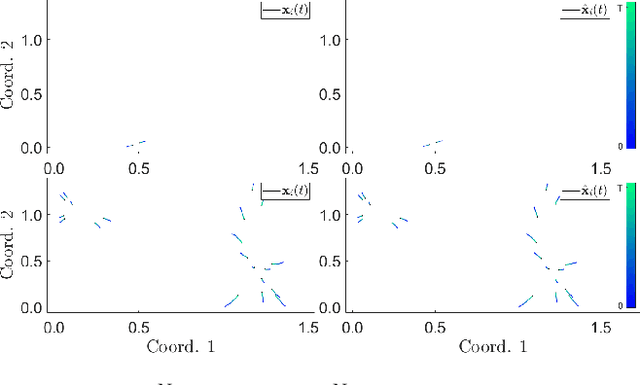
Dynamical systems across many disciplines are modeled as interacting particles or agents, with interaction rules that depend on a very small number of variables (e.g. pairwise distances, pairwise differences of phases, etc...), functions of the state of pairs of agents. Yet, these interaction rules can generate self-organized dynamics, with complex emergent behaviors (clustering, flocking, swarming, etc.). We propose a learning technique that, given observations of states and velocities along trajectories of the agents, yields both the variables upon which the interaction kernel depends and the interaction kernel itself, in a nonparametric fashion. This yields an effective dimension reduction which avoids the curse of dimensionality from the high-dimensional observation data (states and velocities of all the agents). We demonstrate the learning capability of our method to a variety of first-order interacting systems.

Unsupervised learning of observation functions in state-space models by nonparametric moment methods

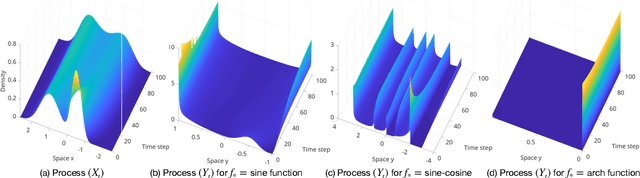
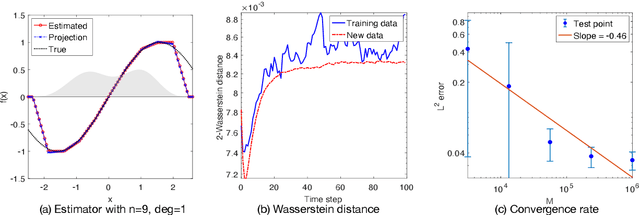
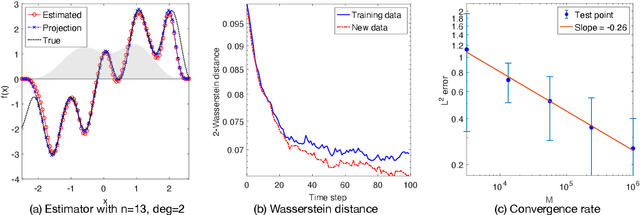
We investigate the unsupervised learning of non-invertible observation functions in nonlinear state-space models. Assuming abundant data of the observation process along with the distribution of the state process, we introduce a nonparametric generalized moment method to estimate the observation function via constrained regression. The major challenge comes from the non-invertibility of the observation function and the lack of data pairs between the state and observation. We address the fundamental issue of identifiability from quadratic loss functionals and show that the function space of identifiability is the closure of a RKHS that is intrinsic to the state process. Numerical results show that the first two moments and temporal correlations, along with upper and lower bounds, can identify functions ranging from piecewise polynomials to smooth functions, leading to convergent estimators. The limitations of this method, such as non-identifiability due to symmetry and stationarity, are also discussed.