Unsupervised learning of observation functions in state-space models by nonparametric moment methods

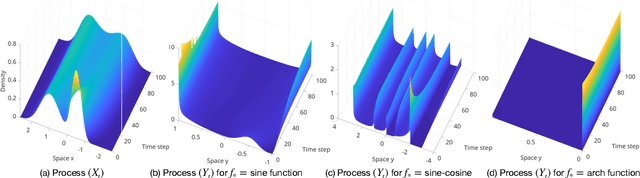
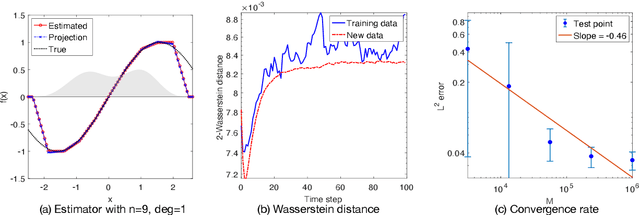
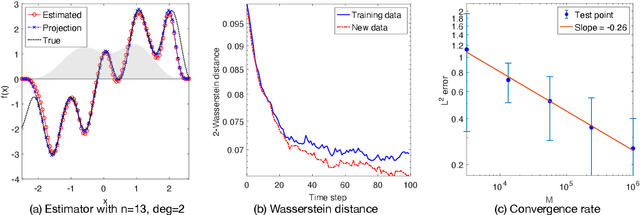
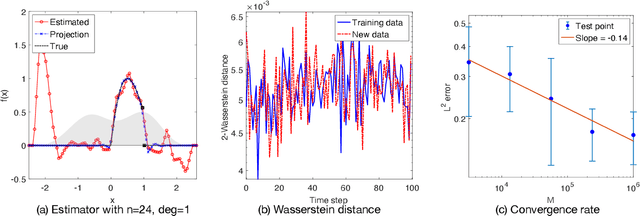
We investigate the unsupervised learning of non-invertible observation functions in nonlinear state-space models. Assuming abundant data of the observation process along with the distribution of the state process, we introduce a nonparametric generalized moment method to estimate the observation function via constrained regression. The major challenge comes from the non-invertibility of the observation function and the lack of data pairs between the state and observation. We address the fundamental issue of identifiability from quadratic loss functionals and show that the function space of identifiability is the closure of a RKHS that is intrinsic to the state process. Numerical results show that the first two moments and temporal correlations, along with upper and lower bounds, can identify functions ranging from piecewise polynomials to smooth functions, leading to convergent estimators. The limitations of this method, such as non-identifiability due to symmetry and stationarity, are also discussed.

Nonparametric learning of kernels in nonlocal operators

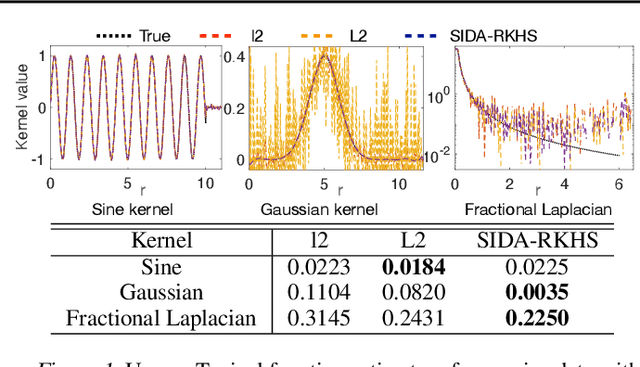
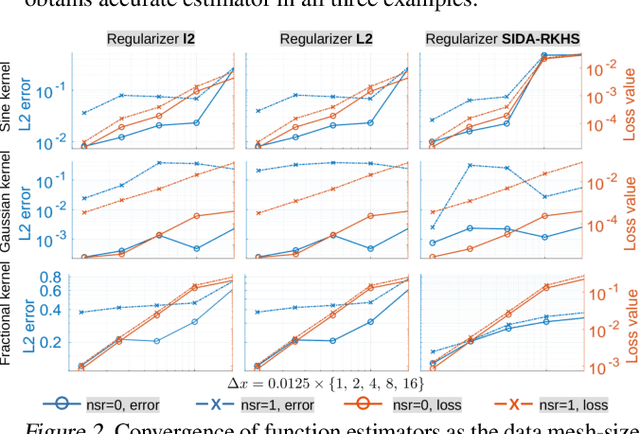
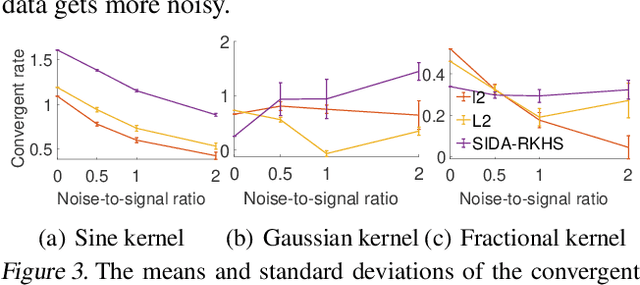
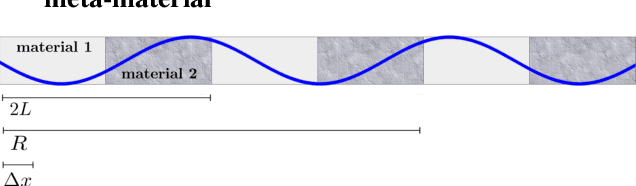
Nonlocal operators with integral kernels have become a popular tool for designing solution maps between function spaces, due to their efficiency in representing long-range dependence and the attractive feature of being resolution-invariant. In this work, we provide a rigorous identifiability analysis and convergence study for the learning of kernels in nonlocal operators. It is found that the kernel learning is an ill-posed or even ill-defined inverse problem, leading to divergent estimators in the presence of modeling errors or measurement noises. To resolve this issue, we propose a nonparametric regression algorithm with a novel data adaptive RKHS Tikhonov regularization method based on the function space of identifiability. The method yields a noisy-robust convergent estimator of the kernel as the data resolution refines, on both synthetic and real-world datasets. In particular, the method successfully learns a homogenized model for the stress wave propagation in a heterogeneous solid, revealing the unknown governing laws from real-world data at microscale. Our regularization method outperforms baseline methods in robustness, generalizability and accuracy.

Data adaptive RKHS Tikhonov regularization for learning kernels in operators

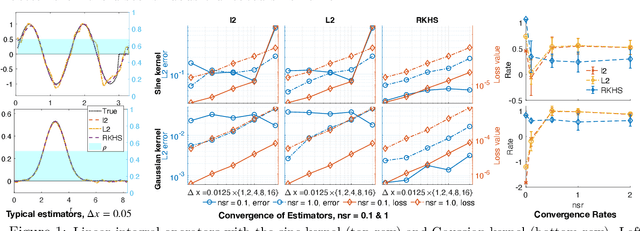
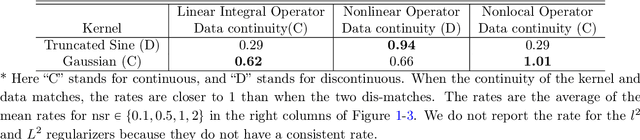
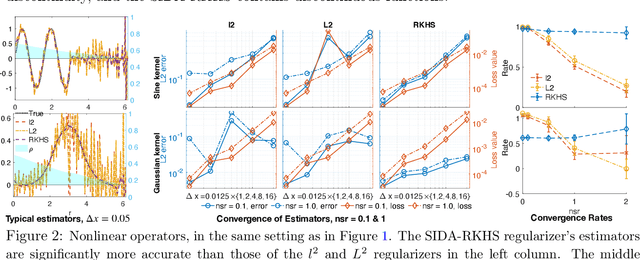
We present DARTR: a Data Adaptive RKHS Tikhonov Regularization method for the linear inverse problem of nonparametric learning of function parameters in operators. A key ingredient is a system intrinsic data-adaptive (SIDA) RKHS, whose norm restricts the learning to take place in the function space of identifiability. DARTR utilizes this norm and selects the regularization parameter by the L-curve method. We illustrate its performance in examples including integral operators, nonlinear operators and nonlocal operators with discrete synthetic data. Numerical results show that DARTR leads to an accurate estimator robust to both numerical error due to discrete data and noise in data, and the estimator converges at a consistent rate as the data mesh refines under different levels of noises, outperforming two baseline regularizers using $l^2$ and $L^2$ norms.