Self-test loss functions for learning weak-form operators and gradient flows

The construction of loss functions presents a major challenge in data-driven modeling involving weak-form operators in PDEs and gradient flows, particularly due to the need to select test functions appropriately. We address this challenge by introducing self-test loss functions, which employ test functions that depend on the unknown parameters, specifically for cases where the operator depends linearly on the unknowns. The proposed self-test loss function conserves energy for gradient flows and coincides with the expected log-likelihood ratio for stochastic differential equations. Importantly, it is quadratic, facilitating theoretical analysis of identifiability and well-posedness of the inverse problem, while also leading to efficient parametric or nonparametric regression algorithms. It is computationally simple, requiring only low-order derivatives or even being entirely derivative-free, and numerical experiments demonstrate its robustness against noisy and discrete data.

Nonlocal Attention Operator: Materializing Hidden Knowledge Towards Interpretable Physics Discovery

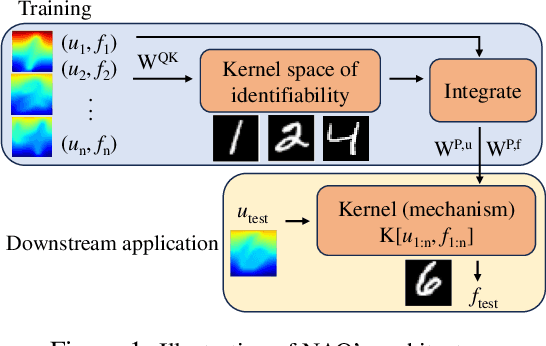
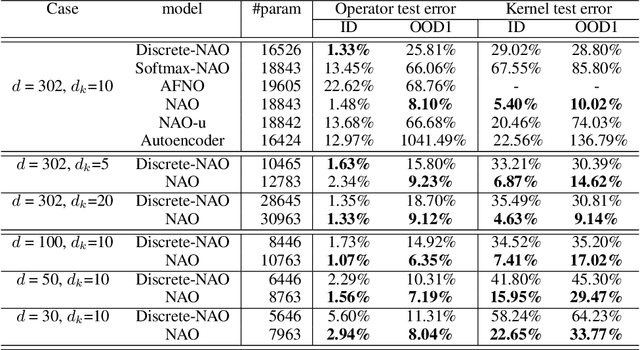
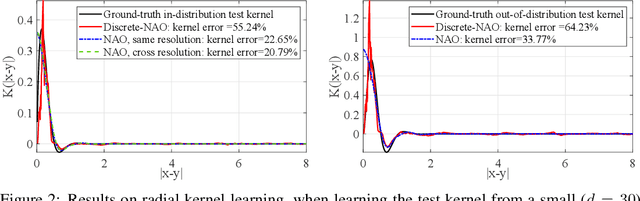
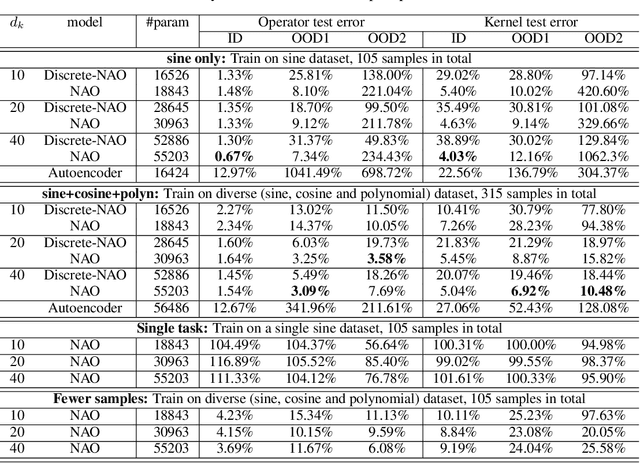
Despite the recent popularity of attention-based neural architectures in core AI fields like natural language processing (NLP) and computer vision (CV), their potential in modeling complex physical systems remains under-explored. Learning problems in physical systems are often characterized as discovering operators that map between function spaces based on a few instances of function pairs. This task frequently presents a severely ill-posed PDE inverse problem. In this work, we propose a novel neural operator architecture based on the attention mechanism, which we coin Nonlocal Attention Operator (NAO), and explore its capability towards developing a foundation physical model. In particular, we show that the attention mechanism is equivalent to a double integral operator that enables nonlocal interactions among spatial tokens, with a data-dependent kernel characterizing the inverse mapping from data to the hidden parameter field of the underlying operator. As such, the attention mechanism extracts global prior information from training data generated by multiple systems, and suggests the exploratory space in the form of a nonlinear kernel map. Consequently, NAO can address ill-posedness and rank deficiency in inverse PDE problems by encoding regularization and achieving generalizability. We empirically demonstrate the advantages of NAO over baseline neural models in terms of generalizability to unseen data resolutions and system states. Our work not only suggests a novel neural operator architecture for learning interpretable foundation models of physical systems, but also offers a new perspective towards understanding the attention mechanism.

MathOdyssey: Benchmarking Mathematical Problem-Solving Skills in Large Language Models Using Odyssey Math Data

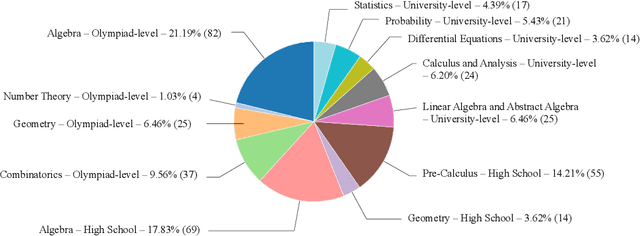
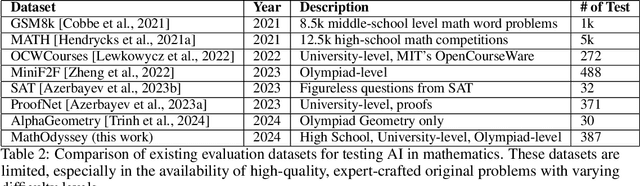
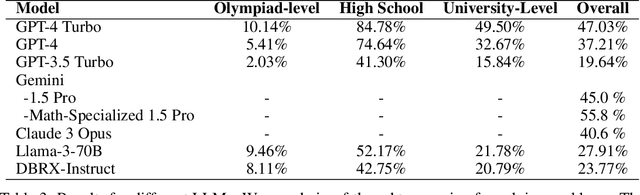
Large language models (LLMs) have significantly advanced natural language understanding and demonstrated strong problem-solving abilities. Despite these successes, most LLMs still struggle with solving mathematical problems due to the intricate reasoning required. This paper investigates the mathematical problem-solving capabilities of LLMs using the newly developed "MathOdyssey" dataset. The dataset includes diverse mathematical problems at high school and university levels, created by experts from notable institutions to rigorously test LLMs in advanced problem-solving scenarios and cover a wider range of subject areas. By providing the MathOdyssey dataset as a resource to the AI community, we aim to contribute to the understanding and improvement of AI capabilities in complex mathematical problem-solving. We conduct benchmarking on open-source models, such as Llama-3 and DBRX-Instruct, and closed-source models from the GPT series and Gemini models. Our results indicate that while LLMs perform well on routine and moderately difficult tasks, they face significant challenges with Olympiad-level problems and complex university-level questions. Our analysis shows a narrowing performance gap between open-source and closed-source models, yet substantial challenges remain, particularly with the most demanding problems. This study highlights the ongoing need for research to enhance the mathematical reasoning of LLMs. The dataset, results, and code are publicly available.

Interacting Particle Systems on Networks: joint inference of the network and the interaction kernel

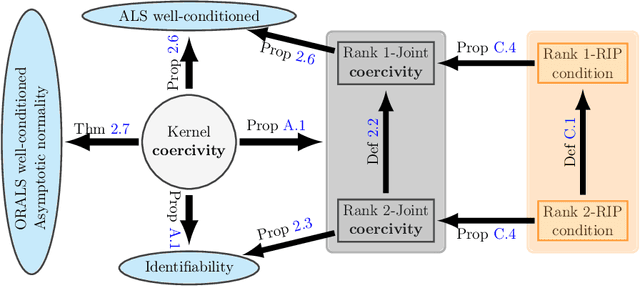
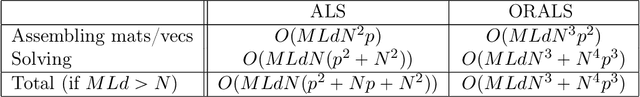
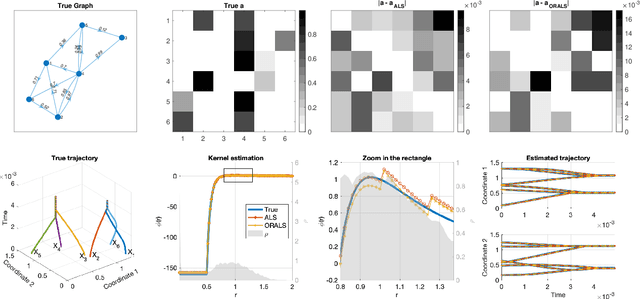
Modeling multi-agent systems on networks is a fundamental challenge in a wide variety of disciplines. We jointly infer the weight matrix of the network and the interaction kernel, which determine respectively which agents interact with which others and the rules of such interactions from data consisting of multiple trajectories. The estimator we propose leads naturally to a non-convex optimization problem, and we investigate two approaches for its solution: one is based on the alternating least squares (ALS) algorithm; another is based on a new algorithm named operator regression with alternating least squares (ORALS). Both algorithms are scalable to large ensembles of data trajectories. We establish coercivity conditions guaranteeing identifiability and well-posedness. The ALS algorithm appears statistically efficient and robust even in the small data regime but lacks performance and convergence guarantees. The ORALS estimator is consistent and asymptotically normal under a coercivity condition. We conduct several numerical experiments ranging from Kuramoto particle systems on networks to opinion dynamics in leader-follower models.

Optimal minimax rate of learning interaction kernels

Nonparametric estimation of nonlocal interaction kernels is crucial in various applications involving interacting particle systems. The inference challenge, situated at the nexus of statistical learning and inverse problems, comes from the nonlocal dependency. A central question is whether the optimal minimax rate of convergence for this problem aligns with the rate of $M^{-\frac{2\beta}{2\beta+1}}$ in classical nonparametric regression, where $M$ is the sample size and $\beta$ represents the smoothness exponent of the radial kernel. Our study confirms this alignment for systems with a finite number of particles. We introduce a tamed least squares estimator (tLSE) that attains the optimal convergence rate for a broad class of exchangeable distributions. The tLSE bridges the smallest eigenvalue of random matrices and Sobolev embedding. This estimator relies on nonasymptotic estimates for the left tail probability of the smallest eigenvalue of the normal matrix. The lower minimax rate is derived using the Fano-Tsybakov hypothesis testing method. Our findings reveal that provided the inverse problem in the large sample limit satisfies a coercivity condition, the left tail probability does not alter the bias-variance tradeoff, and the optimal minimax rate remains intact. Our tLSE method offers a straightforward approach for establishing the optimal minimax rate for models with either local or nonlocal dependency.

Energy-Aware Routing Algorithm for Mobile Ground-to-Air Charging

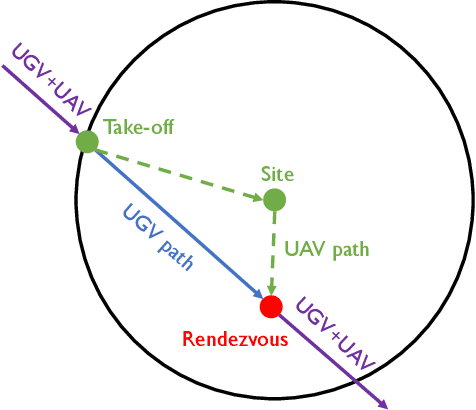
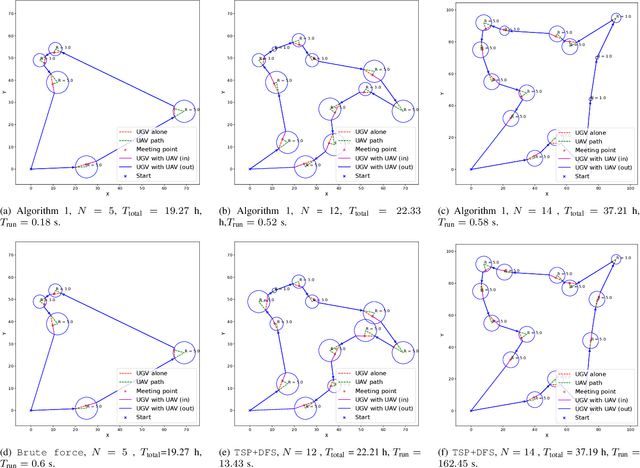
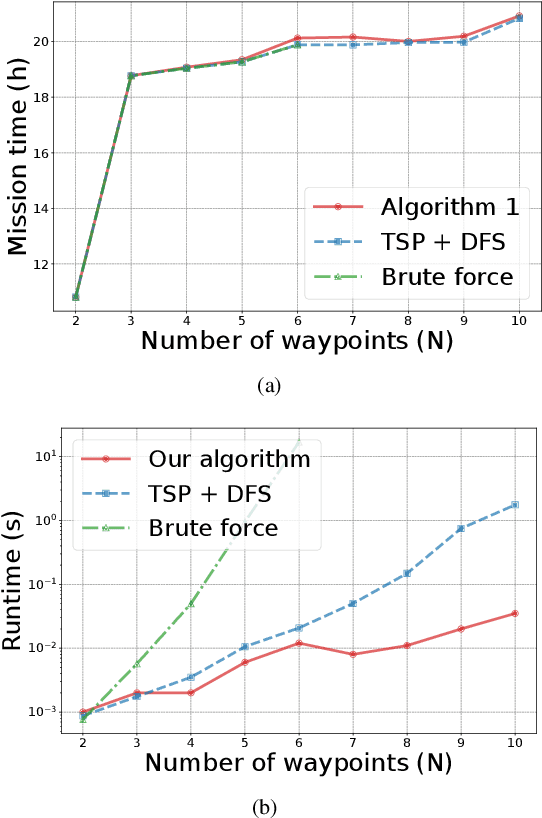
We investigate the problem of energy-constrained planning for a cooperative system of an Unmanned Ground Vehicles (UGV) and an Unmanned Aerial Vehicle (UAV). In scenarios where the UGV serves as a mobile base to ferry the UAV and as a charging station to recharge the UAV, we formulate a novel energy-constrained routing problem. To tackle this problem, we design an energy-aware routing algorithm, aiming to minimize the overall mission duration under the energy limitations of both vehicles. The algorithm first solves a Traveling Salesman Problem (TSP) to generate a guided tour. Then, it employs the Monte-Carlo Tree Search (MCTS) algorithm to refine the tour and generate paths for the two vehicles. We evaluate the performance of our algorithm through extensive simulations and a proof-of-concept experiment. The results show that our algorithm consistently achieves near-optimal mission time and maintains fast running time across a wide range of problem instances.

Small noise analysis for Tikhonov and RKHS regularizations

Regularization plays a pivotal role in ill-posed machine learning and inverse problems. However, the fundamental comparative analysis of various regularization norms remains open. We establish a small noise analysis framework to assess the effects of norms in Tikhonov and RKHS regularizations, in the context of ill-posed linear inverse problems with Gaussian noise. This framework studies the convergence rates of regularized estimators in the small noise limit and reveals the potential instability of the conventional L2-regularizer. We solve such instability by proposing an innovative class of adaptive fractional RKHS regularizers, which covers the L2 Tikhonov and RKHS regularizations by adjusting the fractional smoothness parameter. A surprising insight is that over-smoothing via these fractional RKHSs consistently yields optimal convergence rates, but the optimal hyper-parameter may decay too fast to be selected in practice.

Benchmarking optimality of time series classification methods in distinguishing diffusions

Performance benchmarking is a crucial component of time series classification (TSC) algorithm design, and a fast-growing number of datasets have been established for empirical benchmarking. However, the empirical benchmarks are costly and do not guarantee statistical optimality. This study proposes to benchmark the optimality of TSC algorithms in distinguishing diffusion processes by the likelihood ratio test (LRT). The LRT is optimal in the sense of the Neyman-Pearson lemma: it has the smallest false positive rate among classifiers with a controlled level of false negative rate. The LRT requires the likelihood ratio of the time series to be computable. The diffusion processes from stochastic differential equations provide such time series and are flexible in design for generating linear or nonlinear time series. We demonstrate the benchmarking with three scalable state-of-the-art TSC algorithms: random forest, ResNet, and ROCKET. Test results show that they can achieve LRT optimality for univariate time series and multivariate Gaussian processes. However, these model-agnostic algorithms are suboptimal in classifying nonlinear multivariate time series from high-dimensional stochastic interacting particle systems. Additionally, the LRT benchmark provides tools to analyze the dependence of classification accuracy on the time length, dimension, temporal sampling frequency, and randomness of the time series. Thus, the LRT with diffusion processes can systematically and efficiently benchmark the optimality of TSC algorithms and may guide their future improvements.

A Data-Adaptive Prior for Bayesian Learning of Kernels in Operators

Kernels are efficient in representing nonlocal dependence and they are widely used to design operators between function spaces. Thus, learning kernels in operators from data is an inverse problem of general interest. Due to the nonlocal dependence, the inverse problem can be severely ill-posed with a data-dependent singular inversion operator. The Bayesian approach overcomes the ill-posedness through a non-degenerate prior. However, a fixed non-degenerate prior leads to a divergent posterior mean when the observation noise becomes small, if the data induces a perturbation in the eigenspace of zero eigenvalues of the inversion operator. We introduce a data-adaptive prior to achieve a stable posterior whose mean always has a small noise limit. The data-adaptive prior's covariance is the inversion operator with a hyper-parameter selected adaptive to data by the L-curve method. Furthermore, we provide a detailed analysis on the computational practice of the data-adaptive prior, and demonstrate it on Toeplitz matrices and integral operators. Numerical tests show that a fixed prior can lead to a divergent posterior mean in the presence of any of the four types of errors: discretization error, model error, partial observation and wrong noise assumption. In contrast, the data-adaptive prior always attains posterior means with small noise limits.

Unsupervised learning of observation functions in state-space models by nonparametric moment methods

We investigate the unsupervised learning of non-invertible observation functions in nonlinear state-space models. Assuming abundant data of the observation process along with the distribution of the state process, we introduce a nonparametric generalized moment method to estimate the observation function via constrained regression. The major challenge comes from the non-invertibility of the observation function and the lack of data pairs between the state and observation. We address the fundamental issue of identifiability from quadratic loss functionals and show that the function space of identifiability is the closure of a RKHS that is intrinsic to the state process. Numerical results show that the first two moments and temporal correlations, along with upper and lower bounds, can identify functions ranging from piecewise polynomials to smooth functions, leading to convergent estimators. The limitations of this method, such as non-identifiability due to symmetry and stationarity, are also discussed.