Nonlocal Attention Operator: Materializing Hidden Knowledge Towards Interpretable Physics Discovery

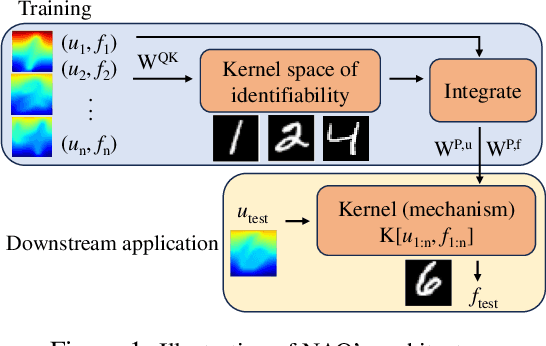
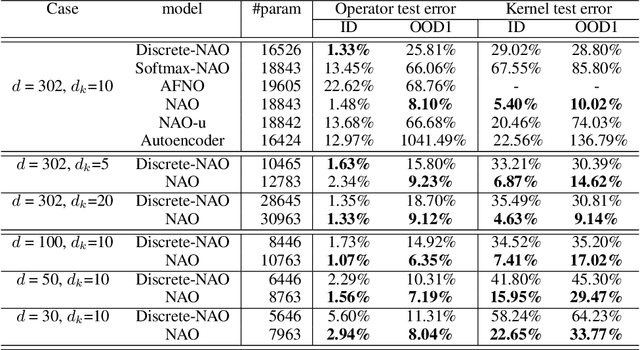
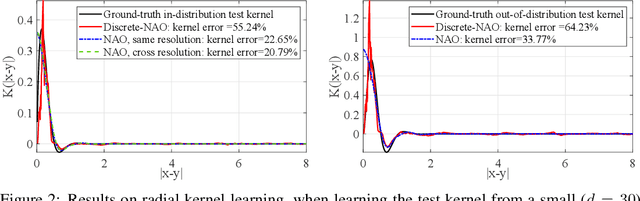
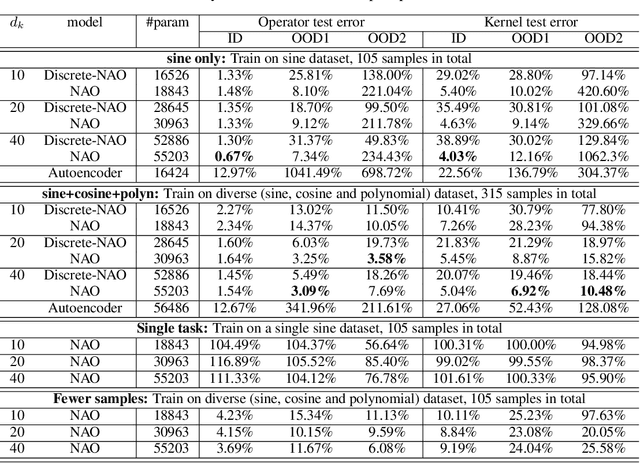
Despite the recent popularity of attention-based neural architectures in core AI fields like natural language processing (NLP) and computer vision (CV), their potential in modeling complex physical systems remains under-explored. Learning problems in physical systems are often characterized as discovering operators that map between function spaces based on a few instances of function pairs. This task frequently presents a severely ill-posed PDE inverse problem. In this work, we propose a novel neural operator architecture based on the attention mechanism, which we coin Nonlocal Attention Operator (NAO), and explore its capability towards developing a foundation physical model. In particular, we show that the attention mechanism is equivalent to a double integral operator that enables nonlocal interactions among spatial tokens, with a data-dependent kernel characterizing the inverse mapping from data to the hidden parameter field of the underlying operator. As such, the attention mechanism extracts global prior information from training data generated by multiple systems, and suggests the exploratory space in the form of a nonlinear kernel map. Consequently, NAO can address ill-posedness and rank deficiency in inverse PDE problems by encoding regularization and achieving generalizability. We empirically demonstrate the advantages of NAO over baseline neural models in terms of generalizability to unseen data resolutions and system states. Our work not only suggests a novel neural operator architecture for learning interpretable foundation models of physical systems, but also offers a new perspective towards understanding the attention mechanism.

Large language models, physics-based modeling, experimental measurements: the trinity of data-scarce learning of polymer properties

Large language models (LLMs) bear promise as a fast and accurate material modeling paradigm for evaluation, analysis, and design. Their vast number of trainable parameters necessitates a wealth of data to achieve accuracy and mitigate overfitting. However, experimental measurements are often limited and costly to obtain in sufficient quantities for finetuning. To this end, we present a physics-based training pipeline that tackles the pathology of data scarcity. The core enabler is a physics-based modeling framework that generates a multitude of synthetic data to align the LLM to a physically consistent initial state before finetuning. Our framework features a two-phase training strategy: (1) utilizing the large-in-amount while less accurate synthetic data for supervised pretraining, and (2) finetuning the phase-1 model with limited experimental data. We empirically demonstrate that supervised pretraining is vital to obtaining accurate finetuned LLMs, via the lens of learning polymer flammability metrics where cone calorimeter data is sparse.

Heterogeneous Peridynamic Neural Operators: Discover Biotissue Constitutive Law and Microstructure From Digital Image Correlation Measurements

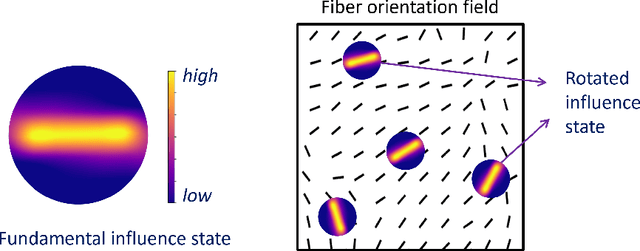
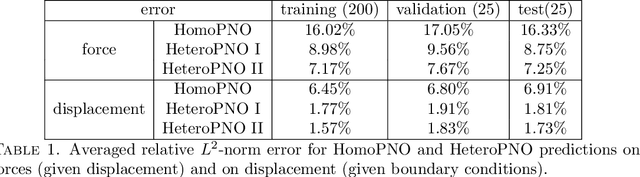
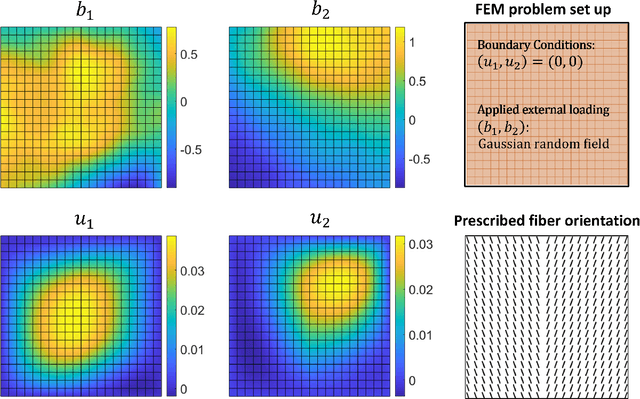
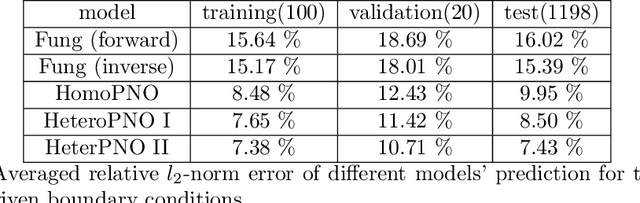
Human tissues are highly organized structures with specific collagen fiber arrangements varying from point to point. The effects of such heterogeneity play an important role for tissue function, and hence it is of critical to discover and understand the distribution of such fiber orientations from experimental measurements, such as the digital image correlation data. To this end, we introduce the heterogeneous peridynamic neural operator (HeteroPNO) approach, for data-driven constitutive modeling of heterogeneous anisotropic materials. The goal is to learn both a nonlocal constitutive law together with the material microstructure, in the form of a heterogeneous fiber orientation field, from loading field-displacement field measurements. To this end, we propose a two-phase learning approach. Firstly, we learn a homogeneous constitutive law in the form of a neural network-based kernel function and a nonlocal bond force, to capture complex homogeneous material responses from data. Then, in the second phase we reinitialize the learnt bond force and the kernel function, and training them together with a fiber orientation field for each material point. Owing to the state-based peridynamic skeleton, our HeteroPNO-learned material models are objective and have the balance of linear and angular momentum guaranteed. Moreover, the effects from heterogeneity and nonlinear constitutive relationship are captured by the kernel function and the bond force respectively, enabling physical interpretability. As a result, our HeteroPNO architecture can learn a constitutive model for a biological tissue with anisotropic heterogeneous response undergoing large deformation regime. Moreover, the framework is capable to provide displacement and stress field predictions for new and unseen loading instances.

Peridynamic Neural Operators: A Data-Driven Nonlocal Constitutive Model for Complex Material Responses

Neural operators, which can act as implicit solution operators of hidden governing equations, have recently become popular tools for learning the responses of complex real-world physical systems. Nevertheless, most neural operator applications have thus far been data-driven and neglect the intrinsic preservation of fundamental physical laws in data. In this work, we introduce a novel integral neural operator architecture called the Peridynamic Neural Operator (PNO) that learns a nonlocal constitutive law from data. This neural operator provides a forward model in the form of state-based peridynamics, with objectivity and momentum balance laws automatically guaranteed. As applications, we demonstrate the expressivity and efficacy of our model in learning complex material behaviors from both synthetic and experimental data sets. We show that, owing to its ability to capture complex responses, our learned neural operator achieves improved accuracy and efficiency compared to baseline models that use predefined constitutive laws. Moreover, by preserving the essential physical laws within the neural network architecture, the PNO is robust in treating noisy data. The method shows generalizability to different domain configurations, external loadings, and discretizations.

Domain Agnostic Fourier Neural Operators

Fourier neural operators (FNOs) can learn highly nonlinear mappings between function spaces, and have recently become a popular tool for learning responses of complex physical systems. However, to achieve good accuracy and efficiency, FNOs rely on the Fast Fourier transform (FFT), which is restricted to modeling problems on rectangular domains. To lift such a restriction and permit FFT on irregular geometries as well as topology changes, we introduce domain agnostic Fourier neural operator (DAFNO), a novel neural operator architecture for learning surrogates with irregular geometries and evolving domains. The key idea is to incorporate a smoothed characteristic function in the integral layer architecture of FNOs, and leverage FFT to achieve rapid computations, in such a way that the geometric information is explicitly encoded in the architecture. In our empirical evaluation, DAFNO has achieved state-of-the-art accuracy as compared to baseline neural operator models on two benchmark datasets of material modeling and airfoil simulation. To further demonstrate the capability and generalizability of DAFNO in handling complex domains with topology changes, we consider a brittle material fracture evolution problem. With only one training crack simulation sample, DAFNO has achieved generalizability to unseen loading scenarios and substantially different crack patterns from the trained scenario.