Stewart Silling
Monotone Peridynamic Neural Operator for Nonlinear Material Modeling with Conditionally Unique Solutions
May 02, 2025



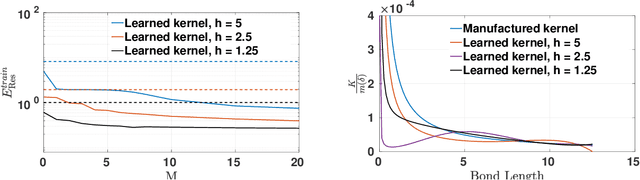
Abstract:Data-driven methods have emerged as powerful tools for modeling the responses of complex nonlinear materials directly from experimental measurements. Among these methods, the data-driven constitutive models present advantages in physical interpretability and generalizability across different boundary conditions/domain settings. However, the well-posedness of these learned models is generally not guaranteed a priori, which makes the models prone to non-physical solutions in downstream simulation tasks. In this study, we introduce monotone peridynamic neural operator (MPNO), a novel data-driven nonlocal constitutive model learning approach based on neural operators. Our approach learns a nonlocal kernel together with a nonlinear constitutive relation, while ensuring solution uniqueness through a monotone gradient network. This architectural constraint on gradient induces convexity of the learnt energy density function, thereby guaranteeing solution uniqueness of MPNO in small deformation regimes. To validate our approach, we evaluate MPNO's performance on both synthetic and real-world datasets. On synthetic datasets with manufactured kernel and constitutive relation, we show that the learnt model converges to the ground-truth as the measurement grid size decreases both theoretically and numerically. Additionally, our MPNO exhibits superior generalization capabilities than the conventional neural networks: it yields smaller displacement solution errors in down-stream tasks with new and unseen loadings. Finally, we showcase the practical utility of our approach through applications in learning a homogenized model from molecular dynamics data, highlighting its expressivity and robustness in real-world scenarios.
Embedded Nonlocal Operator Regression (ENOR): Quantifying model error in learning nonlocal operators
Oct 27, 2024



Abstract:Nonlocal, integral operators have become an efficient surrogate for bottom-up homogenization, due to their ability to represent long-range dependence and multiscale effects. However, the nonlocal homogenized model has unavoidable discrepancy from the microscale model. Such errors accumulate and propagate in long-term simulations, making the resultant prediction unreliable. To develop a robust and reliable bottom-up homogenization framework, we propose a new framework, which we coin Embedded Nonlocal Operator Regression (ENOR), to learn a nonlocal homogenized surrogate model and its structural model error. This framework provides discrepancy-adaptive uncertainty quantification for homogenized material response predictions in long-term simulations. The method is built on Nonlocal Operator Regression (NOR), an optimization-based nonlocal kernel learning approach, together with an embedded model error term in the trainable kernel. Then, Bayesian inference is employed to infer the model error term parameters together with the kernel parameters. To make the problem computationally feasible, we use a multilevel delayed acceptance Markov chain Monte Carlo (MLDA-MCMC) method, enabling efficient Bayesian model calibration and model error estimation. We apply this technique to predict long-term wave propagation in a heterogeneous one-dimensional bar, and compare its performance with additive noise models. Owing to its ability to capture model error, the learned ENOR achieves improved estimation of posterior predictive uncertainty.
Nonlocal Attention Operator: Materializing Hidden Knowledge Towards Interpretable Physics Discovery
Aug 14, 2024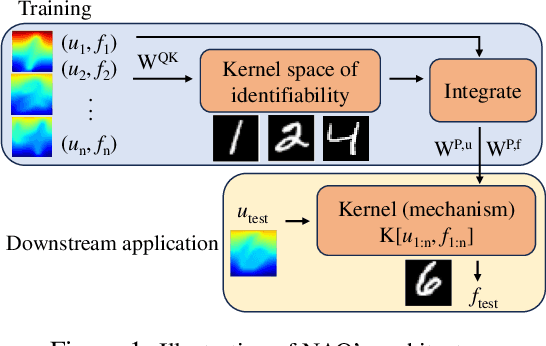
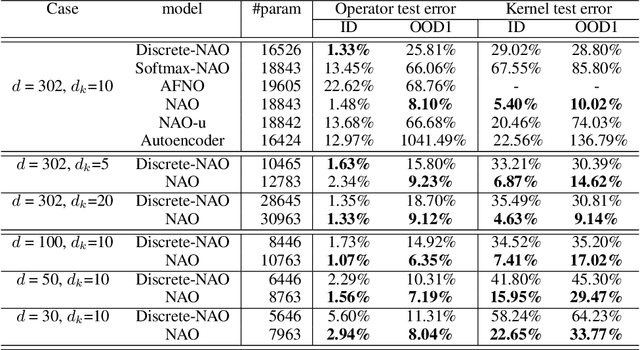
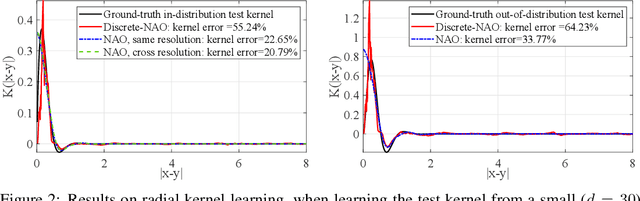
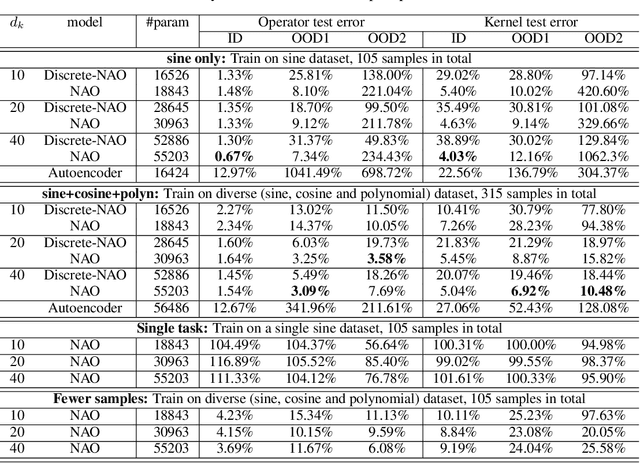
Abstract:Despite the recent popularity of attention-based neural architectures in core AI fields like natural language processing (NLP) and computer vision (CV), their potential in modeling complex physical systems remains under-explored. Learning problems in physical systems are often characterized as discovering operators that map between function spaces based on a few instances of function pairs. This task frequently presents a severely ill-posed PDE inverse problem. In this work, we propose a novel neural operator architecture based on the attention mechanism, which we coin Nonlocal Attention Operator (NAO), and explore its capability towards developing a foundation physical model. In particular, we show that the attention mechanism is equivalent to a double integral operator that enables nonlocal interactions among spatial tokens, with a data-dependent kernel characterizing the inverse mapping from data to the hidden parameter field of the underlying operator. As such, the attention mechanism extracts global prior information from training data generated by multiple systems, and suggests the exploratory space in the form of a nonlinear kernel map. Consequently, NAO can address ill-posedness and rank deficiency in inverse PDE problems by encoding regularization and achieving generalizability. We empirically demonstrate the advantages of NAO over baseline neural models in terms of generalizability to unseen data resolutions and system states. Our work not only suggests a novel neural operator architecture for learning interpretable foundation models of physical systems, but also offers a new perspective towards understanding the attention mechanism.
Heterogeneous Peridynamic Neural Operators: Discover Biotissue Constitutive Law and Microstructure From Digital Image Correlation Measurements
Mar 27, 2024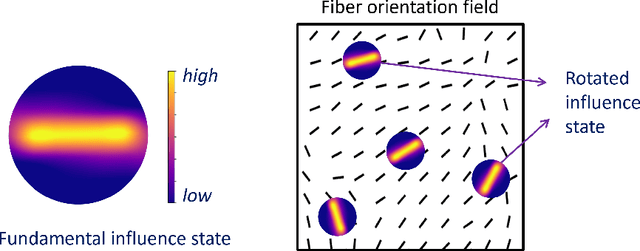
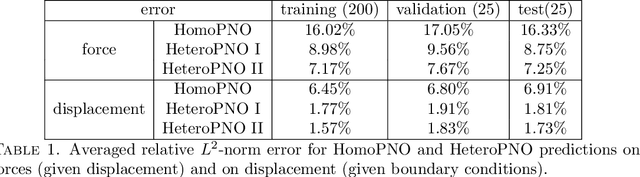
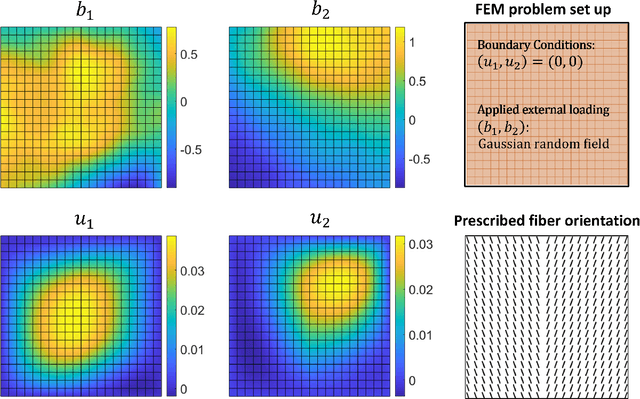
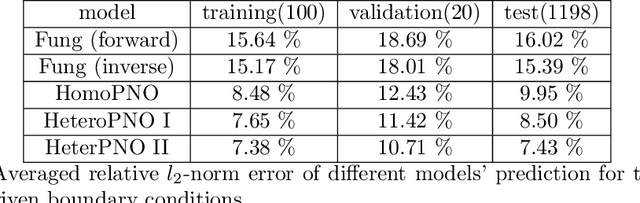
Abstract:Human tissues are highly organized structures with specific collagen fiber arrangements varying from point to point. The effects of such heterogeneity play an important role for tissue function, and hence it is of critical to discover and understand the distribution of such fiber orientations from experimental measurements, such as the digital image correlation data. To this end, we introduce the heterogeneous peridynamic neural operator (HeteroPNO) approach, for data-driven constitutive modeling of heterogeneous anisotropic materials. The goal is to learn both a nonlocal constitutive law together with the material microstructure, in the form of a heterogeneous fiber orientation field, from loading field-displacement field measurements. To this end, we propose a two-phase learning approach. Firstly, we learn a homogeneous constitutive law in the form of a neural network-based kernel function and a nonlocal bond force, to capture complex homogeneous material responses from data. Then, in the second phase we reinitialize the learnt bond force and the kernel function, and training them together with a fiber orientation field for each material point. Owing to the state-based peridynamic skeleton, our HeteroPNO-learned material models are objective and have the balance of linear and angular momentum guaranteed. Moreover, the effects from heterogeneity and nonlinear constitutive relationship are captured by the kernel function and the bond force respectively, enabling physical interpretability. As a result, our HeteroPNO architecture can learn a constitutive model for a biological tissue with anisotropic heterogeneous response undergoing large deformation regime. Moreover, the framework is capable to provide displacement and stress field predictions for new and unseen loading instances.
Peridynamic Neural Operators: A Data-Driven Nonlocal Constitutive Model for Complex Material Responses
Jan 11, 2024Abstract:Neural operators, which can act as implicit solution operators of hidden governing equations, have recently become popular tools for learning the responses of complex real-world physical systems. Nevertheless, most neural operator applications have thus far been data-driven and neglect the intrinsic preservation of fundamental physical laws in data. In this work, we introduce a novel integral neural operator architecture called the Peridynamic Neural Operator (PNO) that learns a nonlocal constitutive law from data. This neural operator provides a forward model in the form of state-based peridynamics, with objectivity and momentum balance laws automatically guaranteed. As applications, we demonstrate the expressivity and efficacy of our model in learning complex material behaviors from both synthetic and experimental data sets. We show that, owing to its ability to capture complex responses, our learned neural operator achieves improved accuracy and efficiency compared to baseline models that use predefined constitutive laws. Moreover, by preserving the essential physical laws within the neural network architecture, the PNO is robust in treating noisy data. The method shows generalizability to different domain configurations, external loadings, and discretizations.
Towards a unified nonlocal, peridynamics framework for the coarse-graining of molecular dynamics data with fractures
Jan 11, 2023Abstract:Molecular dynamics (MD) has served as a powerful tool for designing materials with reduced reliance on laboratory testing. However, the use of MD directly to treat the deformation and failure of materials at the mesoscale is still largely beyond reach. Herein, we propose a learning framework to extract a peridynamic model as a mesoscale continuum surrogate from MD simulated material fracture datasets. Firstly, we develop a novel coarse-graining method, to automatically handle the material fracture and its corresponding discontinuities in MD displacement dataset. Inspired by the Weighted Essentially Non-Oscillatory scheme, the key idea lies at an adaptive procedure to automatically choose the locally smoothest stencil, then reconstruct the coarse-grained material displacement field as piecewise smooth solutions containing discontinuities. Then, based on the coarse-grained MD data, a two-phase optimization-based learning approach is proposed to infer the optimal peridynamics model with damage criterion. In the first phase, we identify the optimal nonlocal kernel function from datasets without material damage, to capture the material stiffness properties. Then, in the second phase, the material damage criterion is learnt as a smoothed step function from the data with fractures. As a result, a peridynamics surrogate is obtained. Our peridynamics surrogate model can be employed in further prediction tasks with different grid resolutions from training, and hence allows for substantial reductions in computational cost compared with MD. We illustrate the efficacy of the proposed approach with several numerical tests for single layer graphene. Our tests show that the proposed data-driven model is robust and generalizable: it is capable in modeling the initialization and growth of fractures under discretization and loading settings that are different from the ones used during training.
Nonlocal Kernel Network (NKN): a Stable and Resolution-Independent Deep Neural Network
Jan 06, 2022
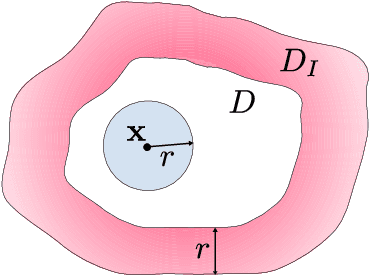

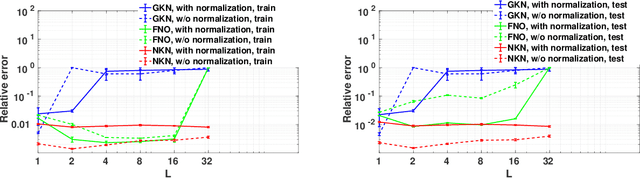
Abstract:Neural operators have recently become popular tools for designing solution maps between function spaces in the form of neural networks. Differently from classical scientific machine learning approaches that learn parameters of a known partial differential equation (PDE) for a single instance of the input parameters at a fixed resolution, neural operators approximate the solution map of a family of PDEs. Despite their success, the uses of neural operators are so far restricted to relatively shallow neural networks and confined to learning hidden governing laws. In this work, we propose a novel nonlocal neural operator, which we refer to as nonlocal kernel network (NKN), that is resolution independent, characterized by deep neural networks, and capable of handling a variety of tasks such as learning governing equations and classifying images. Our NKN stems from the interpretation of the neural network as a discrete nonlocal diffusion reaction equation that, in the limit of infinite layers, is equivalent to a parabolic nonlocal equation, whose stability is analyzed via nonlocal vector calculus. The resemblance with integral forms of neural operators allows NKNs to capture long-range dependencies in the feature space, while the continuous treatment of node-to-node interactions makes NKNs resolution independent. The resemblance with neural ODEs, reinterpreted in a nonlocal sense, and the stable network dynamics between layers allow for generalization of NKN's optimal parameters from shallow to deep networks. This fact enables the use of shallow-to-deep initialization techniques. Our tests show that NKNs outperform baseline methods in both learning governing equations and image classification tasks and generalize well to different resolutions and depths.
A data-driven peridynamic continuum model for upscaling molecular dynamics
Aug 04, 2021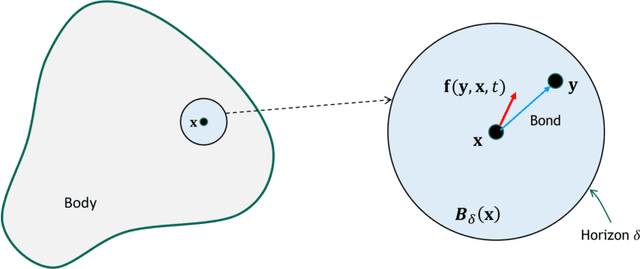

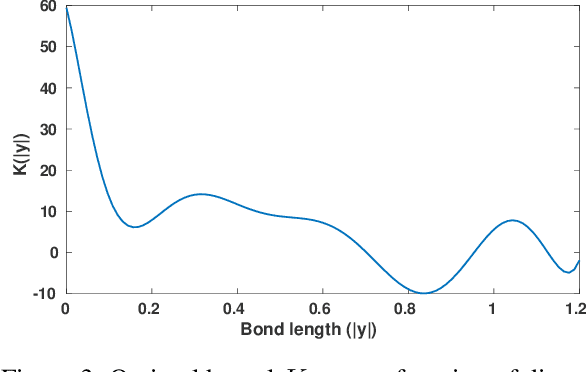
Abstract:Nonlocal models, including peridynamics, often use integral operators that embed lengthscales in their definition. However, the integrands in these operators are difficult to define from the data that are typically available for a given physical system, such as laboratory mechanical property tests. In contrast, molecular dynamics (MD) does not require these integrands, but it suffers from computational limitations in the length and time scales it can address. To combine the strengths of both methods and to obtain a coarse-grained, homogenized continuum model that efficiently and accurately captures materials' behavior, we propose a learning framework to extract, from MD data, an optimal Linear Peridynamic Solid (LPS) model as a surrogate for MD displacements. To maximize the accuracy of the learnt model we allow the peridynamic influence function to be partially negative, while preserving the well-posedness of the resulting model. To achieve this, we provide sufficient well-posedness conditions for discretized LPS models with sign-changing influence functions and develop a constrained optimization algorithm that minimizes the equation residual while enforcing such solvability conditions. This framework guarantees that the resulting model is mathematically well-posed, physically consistent, and that it generalizes well to settings that are different from the ones used during training. We illustrate the efficacy of the proposed approach with several numerical tests for single layer graphene. Our two-dimensional tests show the robustness of the proposed algorithm on validation data sets that include thermal noise, different domain shapes and external loadings, and discretizations substantially different from the ones used for training.
Data-driven learning of nonlocal models: from high-fidelity simulations to constitutive laws
Dec 08, 2020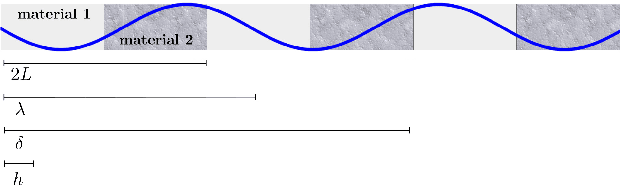
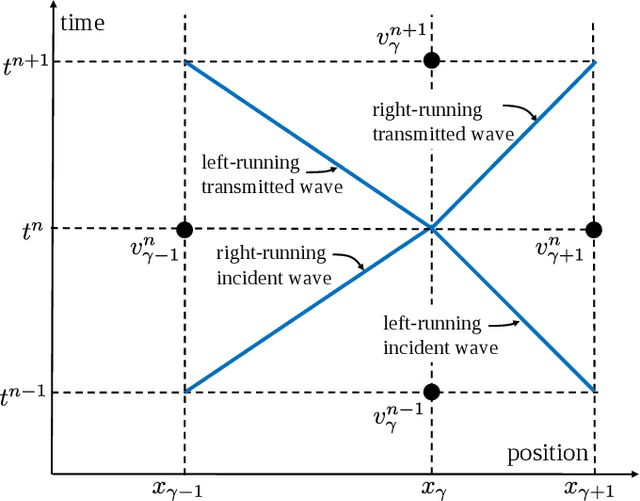
Abstract:We show that machine learning can improve the accuracy of simulations of stress waves in one-dimensional composite materials. We propose a data-driven technique to learn nonlocal constitutive laws for stress wave propagation models. The method is an optimization-based technique in which the nonlocal kernel function is approximated via Bernstein polynomials. The kernel, including both its functional form and parameters, is derived so that when used in a nonlocal solver, it generates solutions that closely match high-fidelity data. The optimal kernel therefore acts as a homogenized nonlocal continuum model that accurately reproduces wave motion in a smaller-scale, more detailed model that can include multiple materials. We apply this technique to wave propagation within a heterogeneous bar with a periodic microstructure. Several one-dimensional numerical tests illustrate the accuracy of our algorithm. The optimal kernel is demonstrated to reproduce high-fidelity data for a composite material in applications that are substantially different from the problems used as training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge