MetaNO: How to Transfer Your Knowledge on Learning Hidden Physics

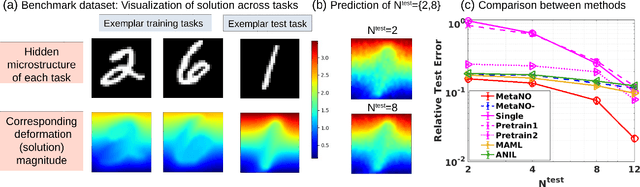
Gradient-based meta-learning methods have primarily been applied to classical machine learning tasks such as image classification. Recently, PDE-solving deep learning methods, such as neural operators, are starting to make an important impact on learning and predicting the response of a complex physical system directly from observational data. Since the data acquisition in this context is commonly challenging and costly, the call of utilization and transfer of existing knowledge to new and unseen physical systems is even more acute. Herein, we propose a novel meta-learning approach for neural operators, which can be seen as transferring the knowledge of solution operators between governing (unknown) PDEs with varying parameter fields. Our approach is a provably universal solution operator for multiple PDE solving tasks, with a key theoretical observation that underlying parameter fields can be captured in the first layer of neural operator models, in contrast to typical final-layer transfer in existing meta-learning methods. As applications, we demonstrate the efficacy of our proposed approach on PDE-based datasets and a real-world material modeling problem, illustrating that our method can handle complex and nonlinear physical response learning tasks while greatly improving the sampling efficiency in unseen tasks.

Towards a unified nonlocal, peridynamics framework for the coarse-graining of molecular dynamics data with fractures

Molecular dynamics (MD) has served as a powerful tool for designing materials with reduced reliance on laboratory testing. However, the use of MD directly to treat the deformation and failure of materials at the mesoscale is still largely beyond reach. Herein, we propose a learning framework to extract a peridynamic model as a mesoscale continuum surrogate from MD simulated material fracture datasets. Firstly, we develop a novel coarse-graining method, to automatically handle the material fracture and its corresponding discontinuities in MD displacement dataset. Inspired by the Weighted Essentially Non-Oscillatory scheme, the key idea lies at an adaptive procedure to automatically choose the locally smoothest stencil, then reconstruct the coarse-grained material displacement field as piecewise smooth solutions containing discontinuities. Then, based on the coarse-grained MD data, a two-phase optimization-based learning approach is proposed to infer the optimal peridynamics model with damage criterion. In the first phase, we identify the optimal nonlocal kernel function from datasets without material damage, to capture the material stiffness properties. Then, in the second phase, the material damage criterion is learnt as a smoothed step function from the data with fractures. As a result, a peridynamics surrogate is obtained. Our peridynamics surrogate model can be employed in further prediction tasks with different grid resolutions from training, and hence allows for substantial reductions in computational cost compared with MD. We illustrate the efficacy of the proposed approach with several numerical tests for single layer graphene. Our tests show that the proposed data-driven model is robust and generalizable: it is capable in modeling the initialization and growth of fractures under discretization and loading settings that are different from the ones used during training.

INO: Invariant Neural Operators for Learning Complex Physical Systems with Momentum Conservation

Neural operators, which emerge as implicit solution operators of hidden governing equations, have recently become popular tools for learning responses of complex real-world physical systems. Nevertheless, the majority of neural operator applications has thus far been data-driven, which neglects the intrinsic preservation of fundamental physical laws in data. In this paper, we introduce a novel integral neural operator architecture, to learn physical models with fundamental conservation laws automatically guaranteed. In particular, by replacing the frame-dependent position information with its invariant counterpart in the kernel space, the proposed neural operator is by design translation- and rotation-invariant, and consequently abides by the conservation laws of linear and angular momentums. As applications, we demonstrate the expressivity and efficacy of our model in learning complex material behaviors from both synthetic and experimental datasets, and show that, by automatically satisfying these essential physical laws, our learned neural operator is not only generalizable in handling translated and rotated datasets, but also achieves state-of-the-art accuracy and efficiency as compared to baseline neural operator models.

MetaNOR: A Meta-Learnt Nonlocal Operator Regression Approach for Metamaterial Modeling

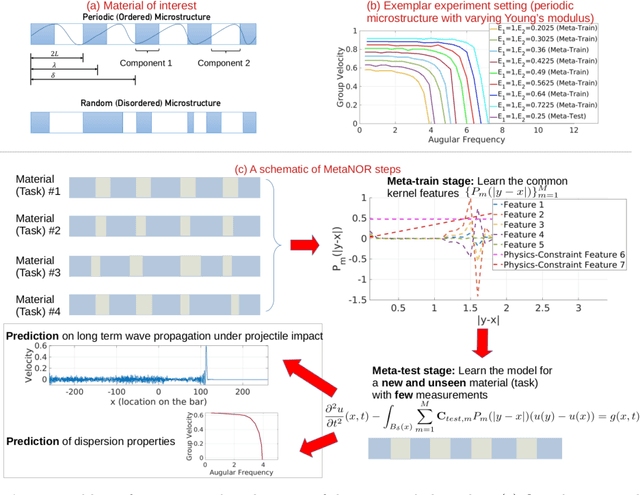
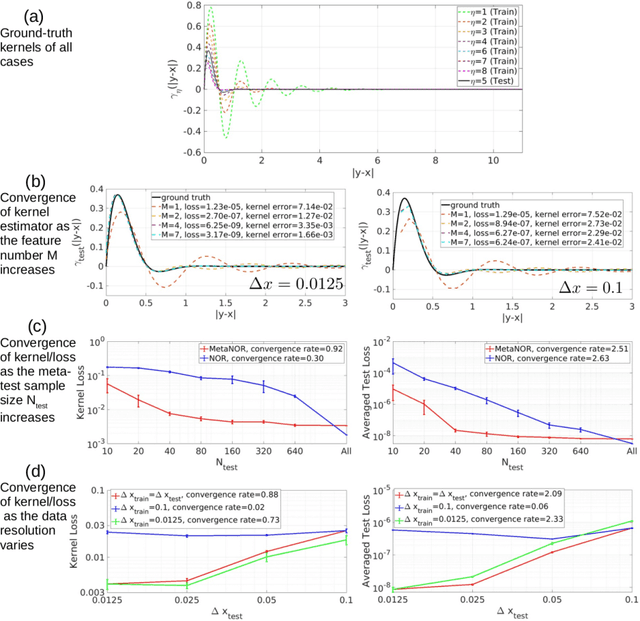
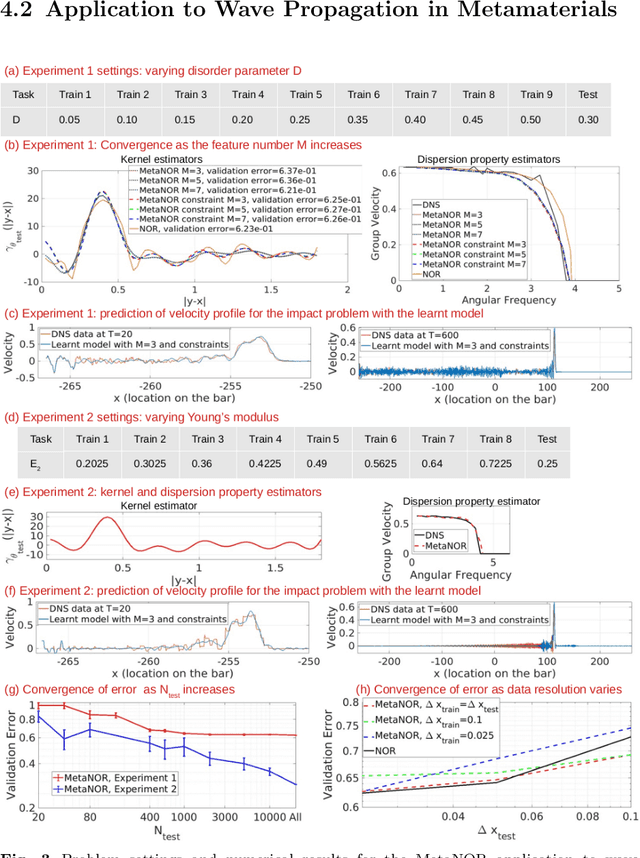
We propose MetaNOR, a meta-learnt approach for transfer-learning operators based on the nonlocal operator regression. The overall goal is to efficiently provide surrogate models for new and unknown material-learning tasks with different microstructures. The algorithm consists of two phases: (1) learning a common nonlocal kernel representation from existing tasks; (2) transferring the learned knowledge and rapidly learning surrogate operators for unseen tasks with a different material, where only a few test samples are required. We apply MetaNOR to model the wave propagation within 1D metamaterials, showing substantial improvements on the sampling efficiency for new materials.

A Physics-Guided Neural Operator Learning Approach to Model Biological Tissues from Digital Image Correlation Measurements

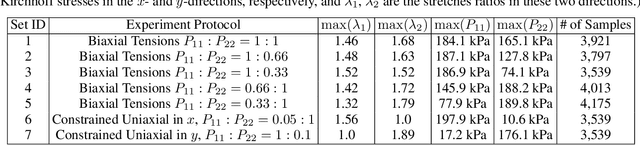
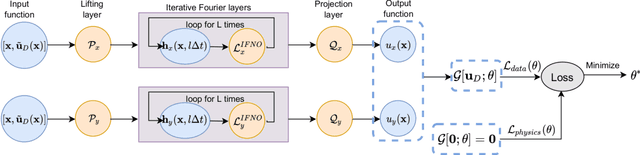
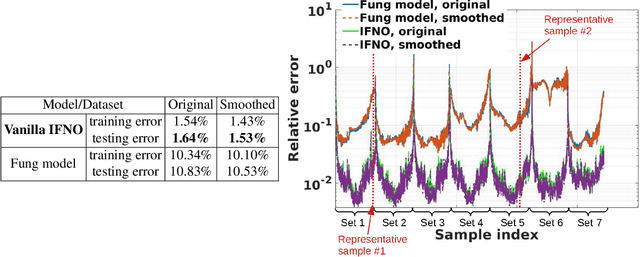
We present a data-driven workflow to biological tissue modeling, which aims to predict the displacement field based on digital image correlation (DIC) measurements under unseen loading scenarios, without postulating a specific constitutive model form nor possessing knowledges on the material microstructure. To this end, a material database is constructed from the DIC displacement tracking measurements of multiple biaxial stretching protocols on a porcine tricuspid valve anterior leaflet, with which we build a neural operator learning model. The material response is modeled as a solution operator from the loading to the resultant displacement field, with the material microstructure properties learned implicitly from the data and naturally embedded in the network parameters. Using various combinations of loading protocols, we compare the predictivity of this framework with finite element analysis based on the phenomenological Fung-type model. From in-distribution tests, the predictivity of our approach presents good generalizability to different loading conditions and outperforms the conventional constitutive modeling at approximately one order of magnitude. When tested on out-of-distribution loading ratios, the neural operator learning approach becomes less effective. To improve the generalizability of our framework, we propose a physics-guided neural operator learning model via imposing partial physics knowledge. This method is shown to improve the model's extrapolative performance in the small-deformation regime. Our results demonstrate that with sufficient data coverage and/or guidance from partial physics constraints, the data-driven approach can be a more effective method for modeling biological materials than the traditional constitutive modeling.

Learning Deep Implicit Fourier Neural Operators (IFNOs) with Applications to Heterogeneous Material Modeling

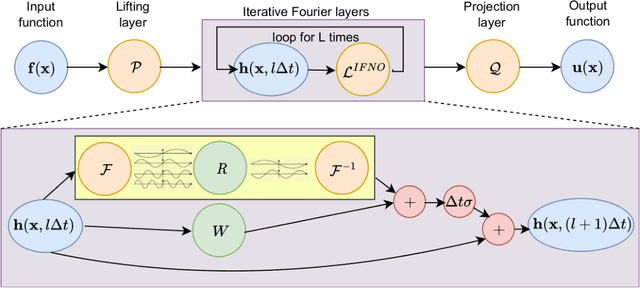
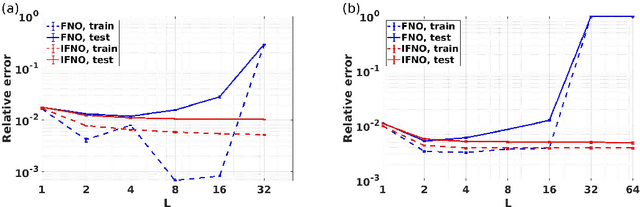
Constitutive modeling based on continuum mechanics theory has been a classical approach for modeling the mechanical responses of materials. However, when constitutive laws are unknown or when defects and/or high degrees of heterogeneity are present, these classical models may become inaccurate. In this work, we propose to use data-driven modeling, which directly utilizes high-fidelity simulation and/or experimental measurements to predict a material's response without using conventional constitutive models. Specifically, the material response is modeled by learning the implicit mappings between loading conditions and the resultant displacement and/or damage fields, with the neural network serving as a surrogate for a solution operator. To model the complex responses due to material heterogeneity and defects, we develop a novel deep neural operator architecture, which we coin as the Implicit Fourier Neural Operator (IFNO). In the IFNO, the increment between layers is modeled as an integral operator to capture the long-range dependencies in the feature space. As the network gets deeper, the limit of IFNO becomes a fixed point equation that yields an implicit neural operator and naturally mimics the displacement/damage fields solving procedure in material modeling problems. We demonstrate the performance of our proposed method for a number of examples, including hyperelastic, anisotropic and brittle materials. As an application, we further employ the proposed approach to learn the material models directly from digital image correlation (DIC) tracking measurements, and show that the learned solution operators substantially outperform the conventional constitutive models in predicting displacement fields.

Nonlocal Kernel Network (NKN): a Stable and Resolution-Independent Deep Neural Network

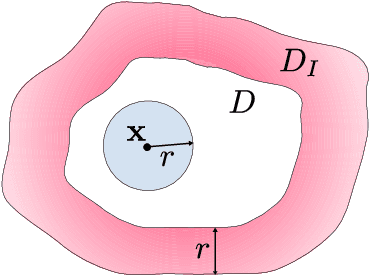
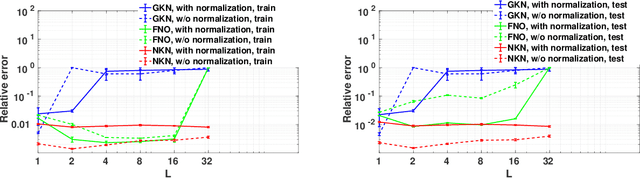
Neural operators have recently become popular tools for designing solution maps between function spaces in the form of neural networks. Differently from classical scientific machine learning approaches that learn parameters of a known partial differential equation (PDE) for a single instance of the input parameters at a fixed resolution, neural operators approximate the solution map of a family of PDEs. Despite their success, the uses of neural operators are so far restricted to relatively shallow neural networks and confined to learning hidden governing laws. In this work, we propose a novel nonlocal neural operator, which we refer to as nonlocal kernel network (NKN), that is resolution independent, characterized by deep neural networks, and capable of handling a variety of tasks such as learning governing equations and classifying images. Our NKN stems from the interpretation of the neural network as a discrete nonlocal diffusion reaction equation that, in the limit of infinite layers, is equivalent to a parabolic nonlocal equation, whose stability is analyzed via nonlocal vector calculus. The resemblance with integral forms of neural operators allows NKNs to capture long-range dependencies in the feature space, while the continuous treatment of node-to-node interactions makes NKNs resolution independent. The resemblance with neural ODEs, reinterpreted in a nonlocal sense, and the stable network dynamics between layers allow for generalization of NKN's optimal parameters from shallow to deep networks. This fact enables the use of shallow-to-deep initialization techniques. Our tests show that NKNs outperform baseline methods in both learning governing equations and image classification tasks and generalize well to different resolutions and depths.

A data-driven peridynamic continuum model for upscaling molecular dynamics

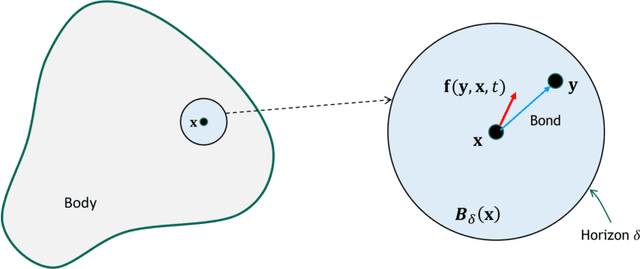
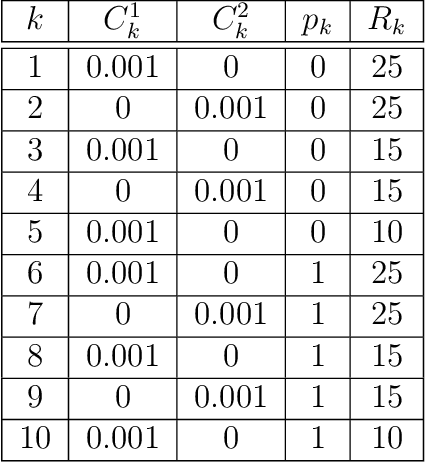
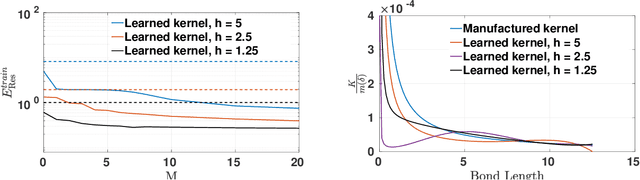
Nonlocal models, including peridynamics, often use integral operators that embed lengthscales in their definition. However, the integrands in these operators are difficult to define from the data that are typically available for a given physical system, such as laboratory mechanical property tests. In contrast, molecular dynamics (MD) does not require these integrands, but it suffers from computational limitations in the length and time scales it can address. To combine the strengths of both methods and to obtain a coarse-grained, homogenized continuum model that efficiently and accurately captures materials' behavior, we propose a learning framework to extract, from MD data, an optimal Linear Peridynamic Solid (LPS) model as a surrogate for MD displacements. To maximize the accuracy of the learnt model we allow the peridynamic influence function to be partially negative, while preserving the well-posedness of the resulting model. To achieve this, we provide sufficient well-posedness conditions for discretized LPS models with sign-changing influence functions and develop a constrained optimization algorithm that minimizes the equation residual while enforcing such solvability conditions. This framework guarantees that the resulting model is mathematically well-posed, physically consistent, and that it generalizes well to settings that are different from the ones used during training. We illustrate the efficacy of the proposed approach with several numerical tests for single layer graphene. Our two-dimensional tests show the robustness of the proposed algorithm on validation data sets that include thermal noise, different domain shapes and external loadings, and discretizations substantially different from the ones used for training.

Data-driven learning of nonlocal models: from high-fidelity simulations to constitutive laws

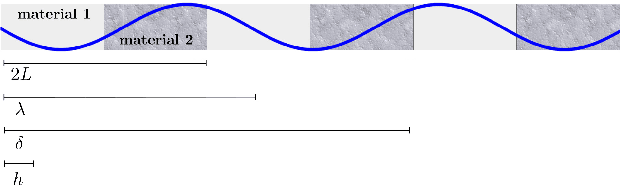
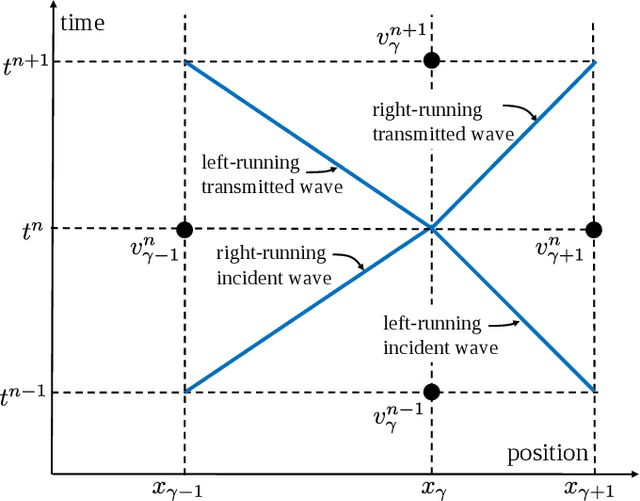
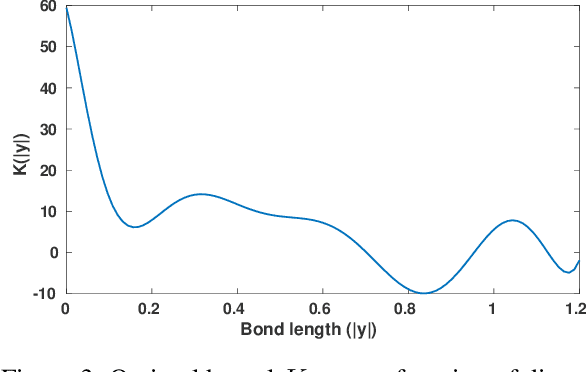
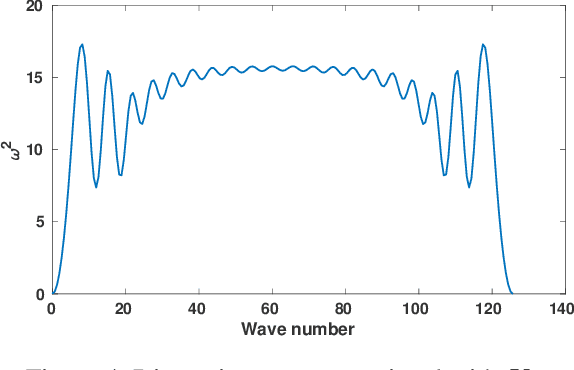
We show that machine learning can improve the accuracy of simulations of stress waves in one-dimensional composite materials. We propose a data-driven technique to learn nonlocal constitutive laws for stress wave propagation models. The method is an optimization-based technique in which the nonlocal kernel function is approximated via Bernstein polynomials. The kernel, including both its functional form and parameters, is derived so that when used in a nonlocal solver, it generates solutions that closely match high-fidelity data. The optimal kernel therefore acts as a homogenized nonlocal continuum model that accurately reproduces wave motion in a smaller-scale, more detailed model that can include multiple materials. We apply this technique to wave propagation within a heterogeneous bar with a periodic microstructure. Several one-dimensional numerical tests illustrate the accuracy of our algorithm. The optimal kernel is demonstrated to reproduce high-fidelity data for a composite material in applications that are substantially different from the problems used as training data.

Data-driven learning of robust nonlocal physics from high-fidelity synthetic data

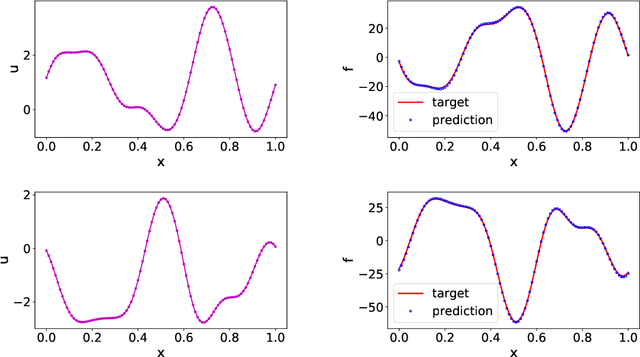
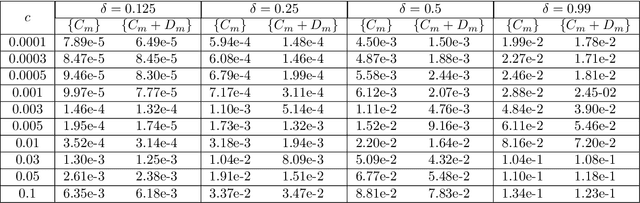
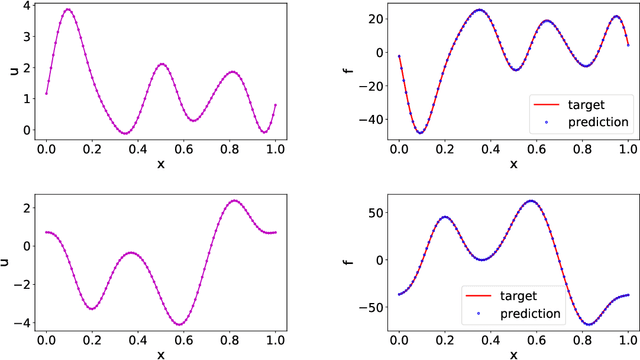
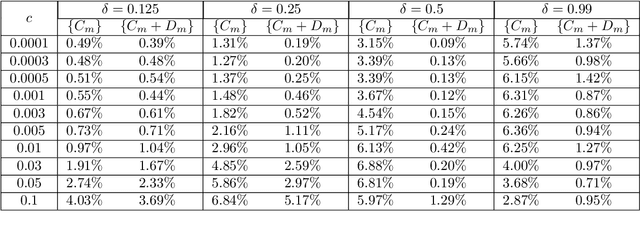
A key challenge to nonlocal models is the analytical complexity of deriving them from first principles, and frequently their use is justified a posteriori. In this work we extract nonlocal models from data, circumventing these challenges and providing data-driven justification for the resulting model form. Extracting provably robust data-driven surrogates is a major challenge for machine learning (ML) approaches, due to nonlinearities and lack of convexity. Our scheme allows extraction of provably invertible nonlocal models whose kernels may be partially negative. To achieve this, based on established nonlocal theory, we embed in our algorithm sufficient conditions on the non-positive part of the kernel that guarantee well-posedness of the learnt operator. These conditions are imposed as inequality constraints and ensure that models are robust, even in small-data regimes. We demonstrate this workflow for a range of applications, including reproduction of manufactured nonlocal kernels; numerical homogenization of Darcy flow associated with a heterogeneous periodic microstructure; nonlocal approximation to high-order local transport phenomena; and approximation of globally supported fractional diffusion operators by truncated kernels.