Heterogeneous Peridynamic Neural Operators: Discover Biotissue Constitutive Law and Microstructure From Digital Image Correlation Measurements

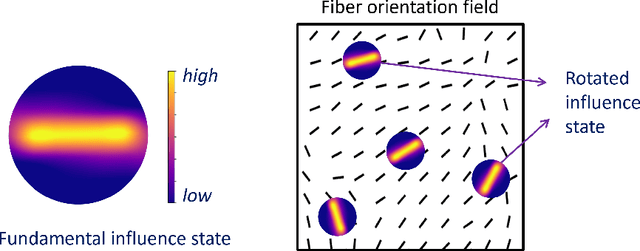
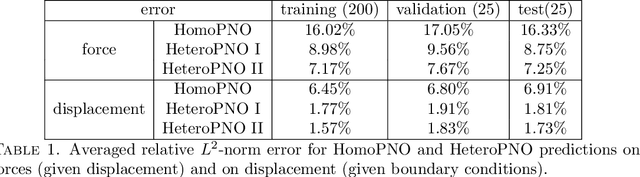
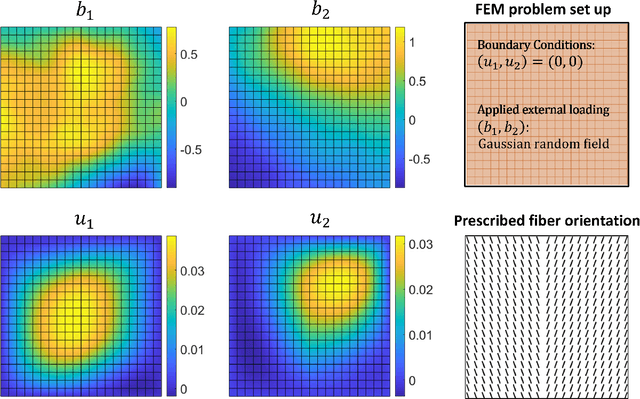
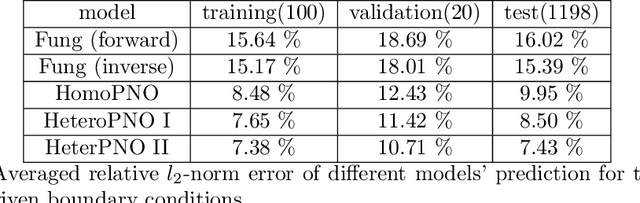
Human tissues are highly organized structures with specific collagen fiber arrangements varying from point to point. The effects of such heterogeneity play an important role for tissue function, and hence it is of critical to discover and understand the distribution of such fiber orientations from experimental measurements, such as the digital image correlation data. To this end, we introduce the heterogeneous peridynamic neural operator (HeteroPNO) approach, for data-driven constitutive modeling of heterogeneous anisotropic materials. The goal is to learn both a nonlocal constitutive law together with the material microstructure, in the form of a heterogeneous fiber orientation field, from loading field-displacement field measurements. To this end, we propose a two-phase learning approach. Firstly, we learn a homogeneous constitutive law in the form of a neural network-based kernel function and a nonlocal bond force, to capture complex homogeneous material responses from data. Then, in the second phase we reinitialize the learnt bond force and the kernel function, and training them together with a fiber orientation field for each material point. Owing to the state-based peridynamic skeleton, our HeteroPNO-learned material models are objective and have the balance of linear and angular momentum guaranteed. Moreover, the effects from heterogeneity and nonlinear constitutive relationship are captured by the kernel function and the bond force respectively, enabling physical interpretability. As a result, our HeteroPNO architecture can learn a constitutive model for a biological tissue with anisotropic heterogeneous response undergoing large deformation regime. Moreover, the framework is capable to provide displacement and stress field predictions for new and unseen loading instances.

MetaNO: How to Transfer Your Knowledge on Learning Hidden Physics

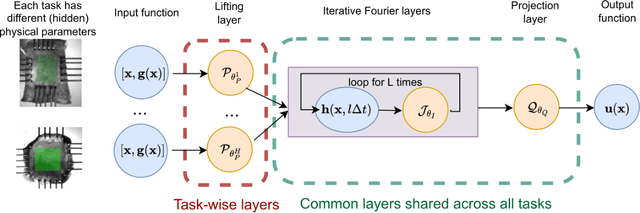
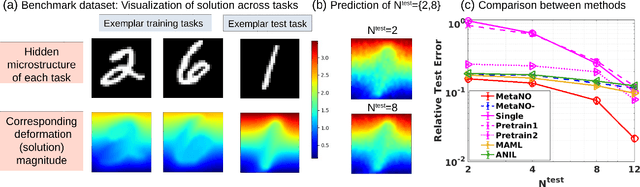
Gradient-based meta-learning methods have primarily been applied to classical machine learning tasks such as image classification. Recently, PDE-solving deep learning methods, such as neural operators, are starting to make an important impact on learning and predicting the response of a complex physical system directly from observational data. Since the data acquisition in this context is commonly challenging and costly, the call of utilization and transfer of existing knowledge to new and unseen physical systems is even more acute. Herein, we propose a novel meta-learning approach for neural operators, which can be seen as transferring the knowledge of solution operators between governing (unknown) PDEs with varying parameter fields. Our approach is a provably universal solution operator for multiple PDE solving tasks, with a key theoretical observation that underlying parameter fields can be captured in the first layer of neural operator models, in contrast to typical final-layer transfer in existing meta-learning methods. As applications, we demonstrate the efficacy of our proposed approach on PDE-based datasets and a real-world material modeling problem, illustrating that our method can handle complex and nonlinear physical response learning tasks while greatly improving the sampling efficiency in unseen tasks.

Anomaly Detection in Driving by Cluster Analysis Twice

Events deviating from normal traffic patterns in driving, anomalies, such as aggressive driving or bumpy roads, may harm delivery efficiency for transportation and logistics (T&L) business. Thus, detecting anomalies in driving is critical for the T&L industry. So far numerous researches have used vehicle sensor data to identify anomalies. Most previous works captured anomalies by using deep learning or machine learning algorithms, which require prior training processes and huge computational costs. This study proposes a method namely Anomaly Detection in Driving by Cluster Analysis Twice (ADDCAT) which clusters the processed sensor data in different physical properties. An event is said to be an anomaly if it never fits with the major cluster, which is considered as the pattern of normality in driving. This method provides a way to detect anomalies in driving with no prior training processes and huge computational costs needed. This paper validated the performance of the method on an open dataset.

A Physics-Guided Neural Operator Learning Approach to Model Biological Tissues from Digital Image Correlation Measurements

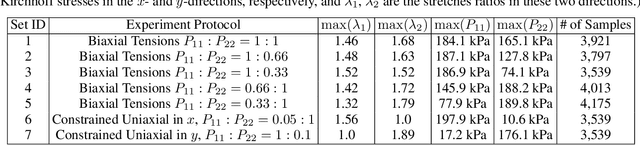
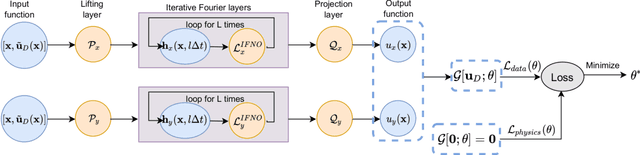
We present a data-driven workflow to biological tissue modeling, which aims to predict the displacement field based on digital image correlation (DIC) measurements under unseen loading scenarios, without postulating a specific constitutive model form nor possessing knowledges on the material microstructure. To this end, a material database is constructed from the DIC displacement tracking measurements of multiple biaxial stretching protocols on a porcine tricuspid valve anterior leaflet, with which we build a neural operator learning model. The material response is modeled as a solution operator from the loading to the resultant displacement field, with the material microstructure properties learned implicitly from the data and naturally embedded in the network parameters. Using various combinations of loading protocols, we compare the predictivity of this framework with finite element analysis based on the phenomenological Fung-type model. From in-distribution tests, the predictivity of our approach presents good generalizability to different loading conditions and outperforms the conventional constitutive modeling at approximately one order of magnitude. When tested on out-of-distribution loading ratios, the neural operator learning approach becomes less effective. To improve the generalizability of our framework, we propose a physics-guided neural operator learning model via imposing partial physics knowledge. This method is shown to improve the model's extrapolative performance in the small-deformation regime. Our results demonstrate that with sufficient data coverage and/or guidance from partial physics constraints, the data-driven approach can be a more effective method for modeling biological materials than the traditional constitutive modeling.

Learning Deep Implicit Fourier Neural Operators (IFNOs) with Applications to Heterogeneous Material Modeling

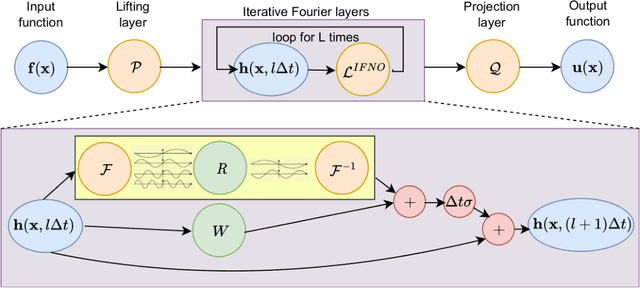
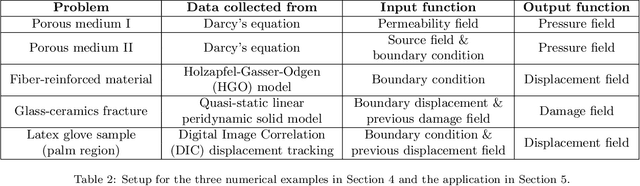
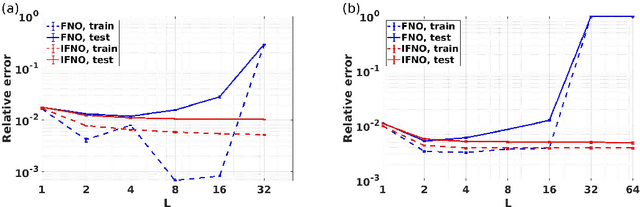
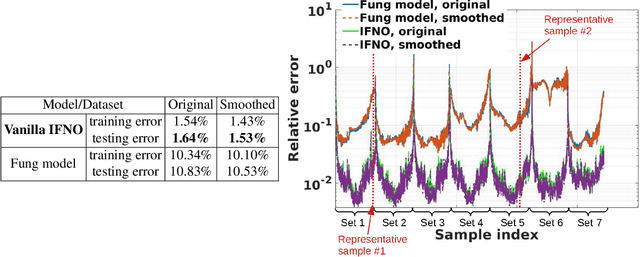
Constitutive modeling based on continuum mechanics theory has been a classical approach for modeling the mechanical responses of materials. However, when constitutive laws are unknown or when defects and/or high degrees of heterogeneity are present, these classical models may become inaccurate. In this work, we propose to use data-driven modeling, which directly utilizes high-fidelity simulation and/or experimental measurements to predict a material's response without using conventional constitutive models. Specifically, the material response is modeled by learning the implicit mappings between loading conditions and the resultant displacement and/or damage fields, with the neural network serving as a surrogate for a solution operator. To model the complex responses due to material heterogeneity and defects, we develop a novel deep neural operator architecture, which we coin as the Implicit Fourier Neural Operator (IFNO). In the IFNO, the increment between layers is modeled as an integral operator to capture the long-range dependencies in the feature space. As the network gets deeper, the limit of IFNO becomes a fixed point equation that yields an implicit neural operator and naturally mimics the displacement/damage fields solving procedure in material modeling problems. We demonstrate the performance of our proposed method for a number of examples, including hyperelastic, anisotropic and brittle materials. As an application, we further employ the proposed approach to learn the material models directly from digital image correlation (DIC) tracking measurements, and show that the learned solution operators substantially outperform the conventional constitutive models in predicting displacement fields.