Data-driven particle dynamics: Structure-preserving coarse-graining for emergent behavior in non-equilibrium systems

Multiscale systems are ubiquitous in science and technology, but are notoriously challenging to simulate as short spatiotemporal scales must be appropriately linked to emergent bulk physics. When expensive high-dimensional dynamical systems are coarse-grained into low-dimensional models, the entropic loss of information leads to emergent physics which are dissipative, history-dependent, and stochastic. To machine learn coarse-grained dynamics from time-series observations of particle trajectories, we propose a framework using the metriplectic bracket formalism that preserves these properties by construction; most notably, the framework guarantees discrete notions of the first and second laws of thermodynamics, conservation of momentum, and a discrete fluctuation-dissipation balance crucial for capturing non-equilibrium statistics. We introduce the mathematical framework abstractly before specializing to a particle discretization. As labels are generally unavailable for entropic state variables, we introduce a novel self-supervised learning strategy to identify emergent structural variables. We validate the method on benchmark systems and demonstrate its utility on two challenging examples: (1) coarse-graining star polymers at challenging levels of coarse-graining while preserving non-equilibrium statistics, and (2) learning models from high-speed video of colloidal suspensions that capture coupling between local rearrangement events and emergent stochastic dynamics. We provide open-source implementations in both PyTorch and LAMMPS, enabling large-scale inference and extensibility to diverse particle-based systems.

Structure-Preserving Digital Twins via Conditional Neural Whitney Forms

We present a framework for constructing real-time digital twins based on structure-preserving reduced finite element models conditioned on a latent variable Z. The approach uses conditional attention mechanisms to learn both a reduced finite element basis and a nonlinear conservation law within the framework of finite element exterior calculus (FEEC). This guarantees numerical well-posedness and exact preservation of conserved quantities, regardless of data sparsity or optimization error. The conditioning mechanism supports real-time calibration to parametric variables, allowing the construction of digital twins which support closed loop inference and calibration to sensor data. The framework interfaces with conventional finite element machinery in a non-invasive manner, allowing treatment of complex geometries and integration of learned models with conventional finite element techniques. Benchmarks include advection diffusion, shock hydrodynamics, electrostatics, and a complex battery thermal runaway problem. The method achieves accurate predictions on complex geometries with sparse data (25 LES simulations), including capturing the transition to turbulence and achieving real-time inference ~0.1s with a speedup of 3.1x10^8 relative to LES. An open-source implementation is available on GitHub.

Gaussian Variational Schemes on Bounded and Unbounded Domains

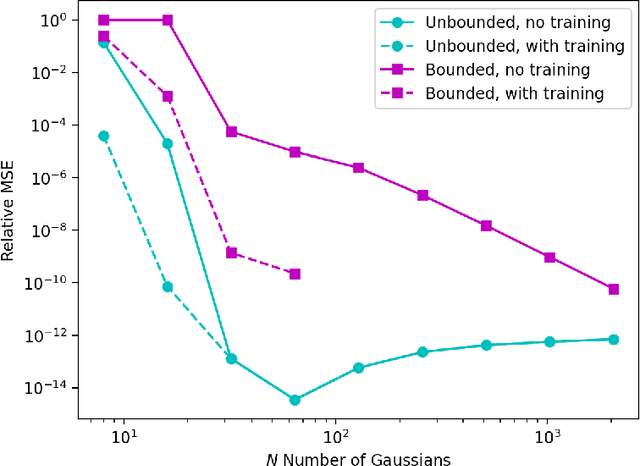
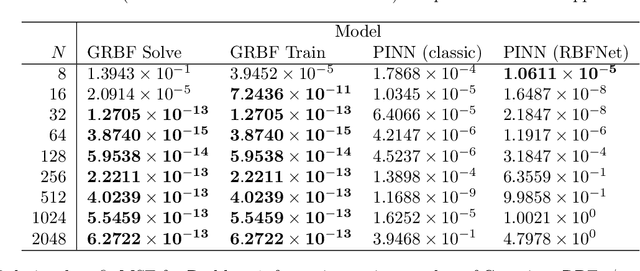
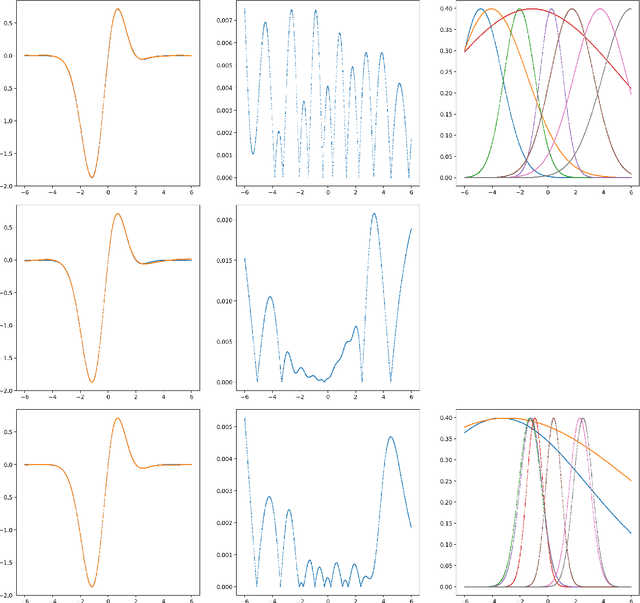
A machine-learnable variational scheme using Gaussian radial basis functions (GRBFs) is presented and used to approximate linear problems on bounded and unbounded domains. In contrast to standard mesh-free methods, which use GRBFs to discretize strong-form differential equations, this work exploits the relationship between integrals of GRBFs, their derivatives, and polynomial moments to produce exact quadrature formulae which enable weak-form expressions. Combined with trainable GRBF means and covariances, this leads to a flexible, generalized Galerkin variational framework which is applied in the infinite-domain setting where the scheme is conforming, as well as the bounded-domain setting where it is not. Error rates for the proposed GRBF scheme are derived in each case, and examples are presented demonstrating utility of this approach as a surrogate modeling technique.

Efficiently Parameterized Neural Metriplectic Systems

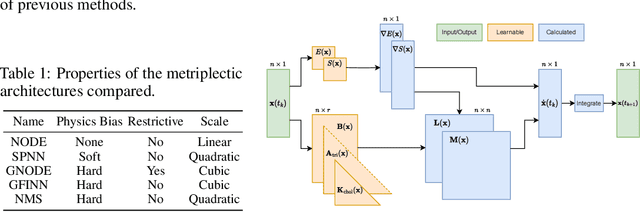
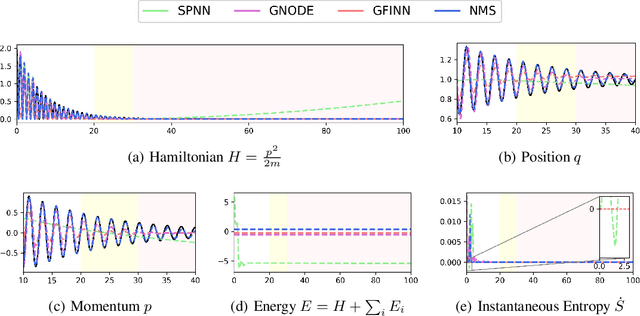
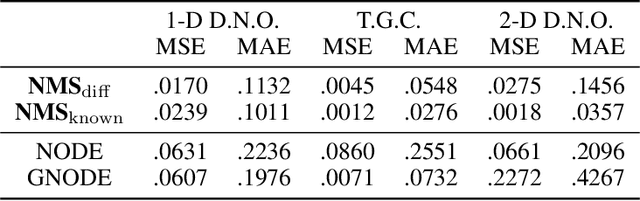
Metriplectic systems are learned from data in a way that scales quadratically in both the size of the state and the rank of the metriplectic data. Besides being provably energy conserving and entropy stable, the proposed approach comes with approximation results demonstrating its ability to accurately learn metriplectic dynamics from data as well as an error estimate indicating its potential for generalization to unseen timescales when approximation error is low. Examples are provided which illustrate performance in the presence of both full state information as well as when entropic variables are unknown, confirming that the proposed approach exhibits superior accuracy and scalability without compromising on model expressivity.

Graph Convolutions Enrich the Self-Attention in Transformers!

Transformers, renowned for their self-attention mechanism, have achieved state-of-the-art performance across various tasks in natural language processing, computer vision, time-series modeling, etc. However, one of the challenges with deep Transformer models is the oversmoothing problem, where representations across layers converge to indistinguishable values, leading to significant performance degradation. We interpret the original self-attention as a simple graph filter and redesign it from a graph signal processing (GSP) perspective. We propose graph-filter-based self-attention (GFSA) to learn a general yet effective one, whose complexity, however, is slightly larger than that of the original self-attention mechanism. We demonstrate that GFSA improves the performance of Transformers in various fields, including computer vision, natural language processing, graph pattern classification, speech recognition, and code classification.

Causal disentanglement of multimodal data

Causal representation learning algorithms discover lower-dimensional representations of data that admit a decipherable interpretation of cause and effect; as achieving such interpretable representations is challenging, many causal learning algorithms utilize elements indicating prior information, such as (linear) structural causal models, interventional data, or weak supervision. Unfortunately, in exploratory causal representation learning, such elements and prior information may not be available or warranted. Alternatively, scientific datasets often have multiple modalities or physics-based constraints, and the use of such scientific, multimodal data has been shown to improve disentanglement in fully unsupervised settings. Consequently, we introduce a causal representation learning algorithm (causalPIMA) that can use multimodal data and known physics to discover important features with causal relationships. Our innovative algorithm utilizes a new differentiable parametrization to learn a directed acyclic graph (DAG) together with a latent space of a variational autoencoder in an end-to-end differentiable framework via a single, tractable evidence lower bound loss function. We place a Gaussian mixture prior on the latent space and identify each of the mixtures with an outcome of the DAG nodes; this novel identification enables feature discovery with causal relationships. Tested against a synthetic and a scientific dataset, our results demonstrate the capability of learning an interpretable causal structure while simultaneously discovering key features in a fully unsupervised setting.

Reversible and irreversible bracket-based dynamics for deep graph neural networks

Recent works have shown that physics-inspired architectures allow the training of deep graph neural networks (GNNs) without oversmoothing. The role of these physics is unclear, however, with successful examples of both reversible (e.g., Hamiltonian) and irreversible (e.g., diffusion) phenomena producing comparable results despite diametrically opposed mechanisms, and further complications arising due to empirical departures from mathematical theory. This work presents a series of novel GNN architectures based upon structure-preserving bracket-based dynamical systems, which are provably guaranteed to either conserve energy or generate positive dissipation with increasing depth. It is shown that the theoretically principled framework employed here allows for inherently explainable constructions, which contextualize departures from theory in current architectures and better elucidate the roles of reversibility and irreversibility in network performance.

Probabilistic partition of unity networks for high-dimensional regression problems

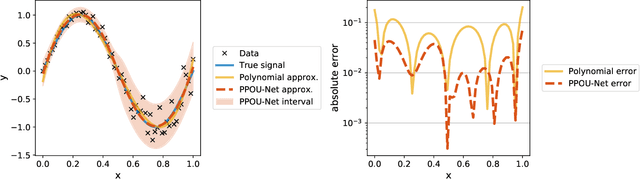
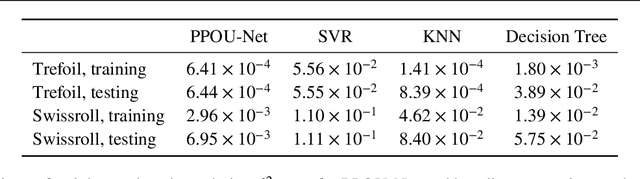
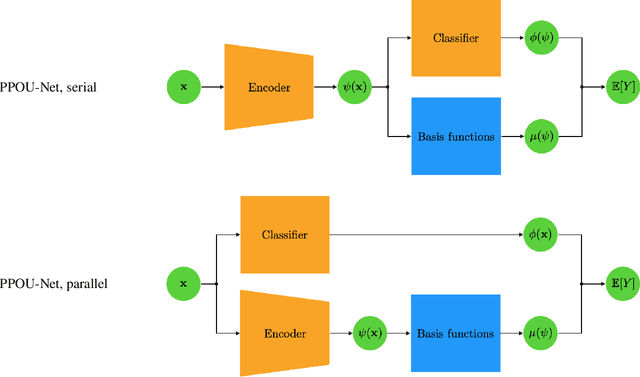
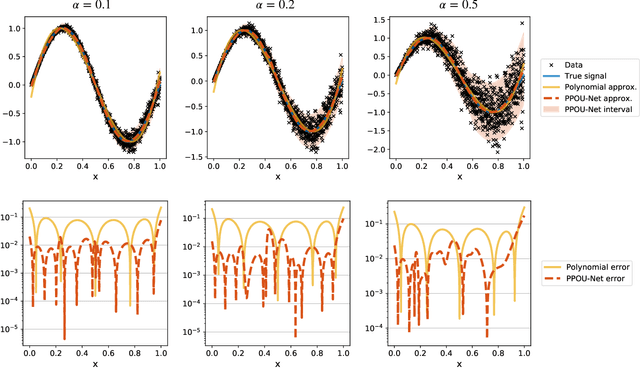
We explore the probabilistic partition of unity network (PPOU-Net) model in the context of high-dimensional regression problems. With the PPOU-Nets, the target function for any given input is approximated by a mixture of experts model, where each cluster is associated with a fixed-degree polynomial. The weights of the clusters are determined by a DNN that defines a partition of unity. The weighted average of the polynomials approximates the target function and produces uncertainty quantification naturally. Our training strategy leverages automatic differentiation and the expectation maximization (EM) algorithm. During the training, we (i) apply gradient descent to update the DNN coefficients; (ii) update the polynomial coefficients using weighted least-squares solves; and (iii) compute the variance of each cluster according to a closed-form formula derived from the EM algorithm. The PPOU-Nets consistently outperform the baseline fully-connected neural networks of comparable sizes in numerical experiments of various data dimensions. We also explore the proposed model in applications of quantum computing, where the PPOU-Nets act as surrogate models for cost landscapes associated with variational quantum circuits.

Parameter-varying neural ordinary differential equations with partition-of-unity networks

In this study, we propose parameter-varying neural ordinary differential equations (NODEs) where the evolution of model parameters is represented by partition-of-unity networks (POUNets), a mixture of experts architecture. The proposed variant of NODEs, synthesized with POUNets, learn a meshfree partition of space and represent the evolution of ODE parameters using sets of polynomials associated to each partition. We demonstrate the effectiveness of the proposed method for three important tasks: data-driven dynamics modeling of (1) hybrid systems, (2) switching linear dynamical systems, and (3) latent dynamics for dynamical systems with varying external forcing.

Scalable algorithms for physics-informed neural and graph networks

Physics-informed machine learning (PIML) has emerged as a promising new approach for simulating complex physical and biological systems that are governed by complex multiscale processes for which some data are also available. In some instances, the objective is to discover part of the hidden physics from the available data, and PIML has been shown to be particularly effective for such problems for which conventional methods may fail. Unlike commercial machine learning where training of deep neural networks requires big data, in PIML big data are not available. Instead, we can train such networks from additional information obtained by employing the physical laws and evaluating them at random points in the space-time domain. Such physics-informed machine learning integrates multimodality and multifidelity data with mathematical models, and implements them using neural networks or graph networks. Here, we review some of the prevailing trends in embedding physics into machine learning, using physics-informed neural networks (PINNs) based primarily on feed-forward neural networks and automatic differentiation. For more complex systems or systems of systems and unstructured data, graph neural networks (GNNs) present some distinct advantages, and here we review how physics-informed learning can be accomplished with GNNs based on graph exterior calculus to construct differential operators; we refer to these architectures as physics-informed graph networks (PIGNs). We present representative examples for both forward and inverse problems and discuss what advances are needed to scale up PINNs, PIGNs and more broadly GNNs for large-scale engineering problems.