Deep Operator Neural Network Model Predictive Control

In this paper, we consider the design of model predictive control (MPC) algorithms based on deep operator neural networks (DeepONets). These neural networks are capable of accurately approximating real and complex valued solutions of continuous time nonlinear systems without relying on recurrent architectures. The DeepONet architecture is made up of two feedforward neural networks: the branch network, which encodes the input function space, and the trunk network, which represents dependencies on temporal variables or initial conditions. Utilizing the original DeepONet architecture as a predictor within MPC for Multi Input Multi Output (MIMO) systems requires multiple branch networks, to generate multi output predictions, one for each input. Moreover, to predict multiple time steps into the future, the network has to be evaluated multiple times. Motivated by this, we introduce a multi step DeepONet (MS-DeepONet) architecture that computes in one shot multi step predictions of system outputs from multi step input sequences, which is better suited for MPC. We prove that the MS DeepONet is a universal approximator in terms of multi step sequence prediction. Additionally, we develop automated hyper parameter selection strategies and implement MPC frameworks using both the standard DeepONet and the proposed MS DeepONet architectures in PyTorch. The implementation is publicly available on GitHub. Simulation results demonstrate that MS-DeepONet consistently outperforms the standard DeepONet in learning and predictive control tasks across several nonlinear benchmark systems: the van der Pol oscillator, the quadruple tank process, and a cart pendulum unstable system, where it successfully learns and executes multiple swing up and stabilization policies.

$PINN - a Domain Decomposition Method for Bayesian Physics-Informed Neural Networks

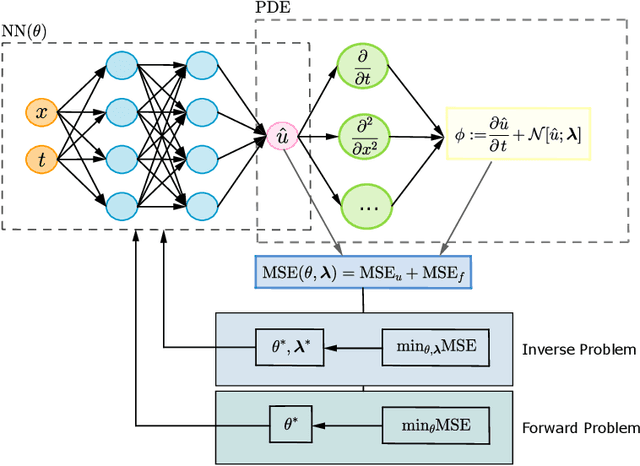
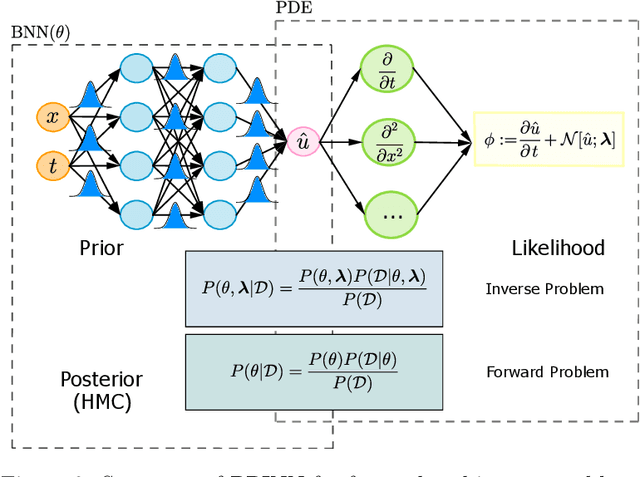
Physics-Informed Neural Networks (PINNs) are a novel computational approach for solving partial differential equations (PDEs) with noisy and sparse initial and boundary data. Although, efficient quantification of epistemic and aleatoric uncertainties in big multi-scale problems remains challenging. We propose \$PINN a novel method of computing global uncertainty in PDEs using a Bayesian framework, by combining local Bayesian Physics-Informed Neural Networks (BPINN) with domain decomposition. The solution continuity across subdomains is obtained by imposing the flux continuity across the interface of neighboring subdomains. To demonstrate the effectiveness of \$PINN, we conduct a series of computational experiments on PDEs in 1D and 2D spatial domains. Although we have adopted conservative PINNs (cPINNs), the method can be seamlessly extended to other domain decomposition techniques. The results infer that the proposed method recovers the global uncertainty by computing the local uncertainty exactly more efficiently as the uncertainty in each subdomain can be computed concurrently. The robustness of \$PINN is verified by adding uncorrelated random noise to the training data up to 15% and testing for different domain sizes.

Leveraging Deep Operator Networks (DeepONet) for Acoustic Full Waveform Inversion (FWI)

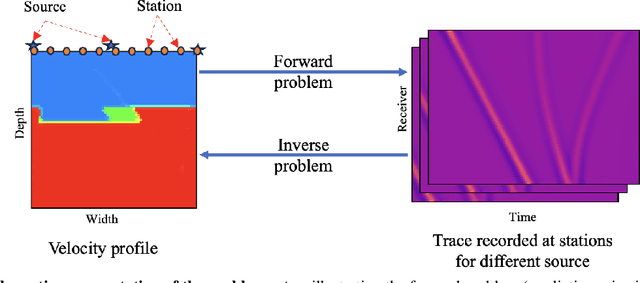
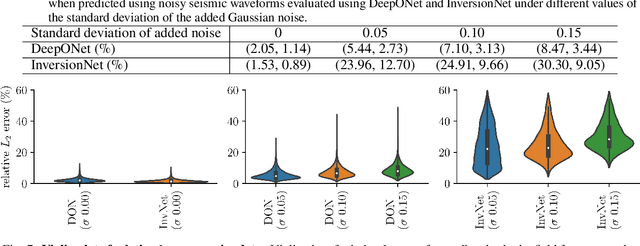
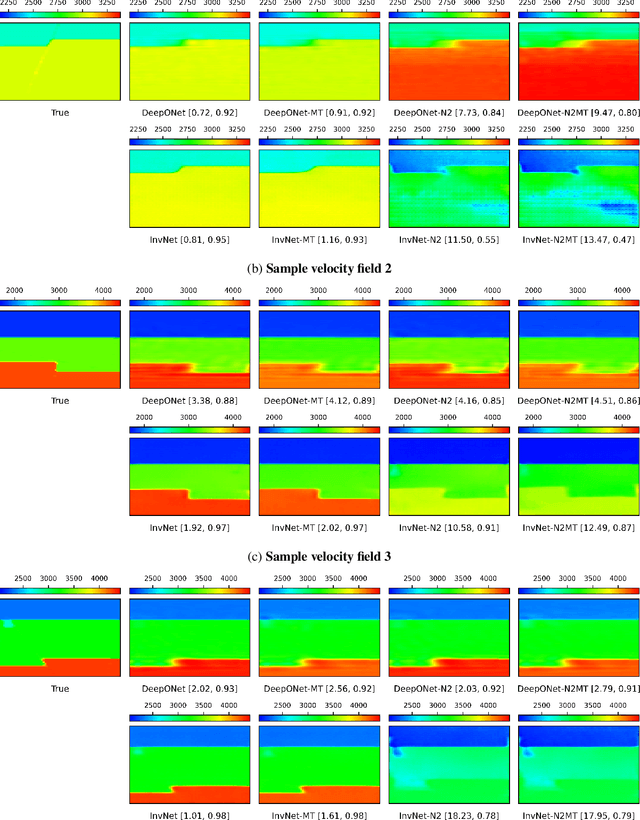
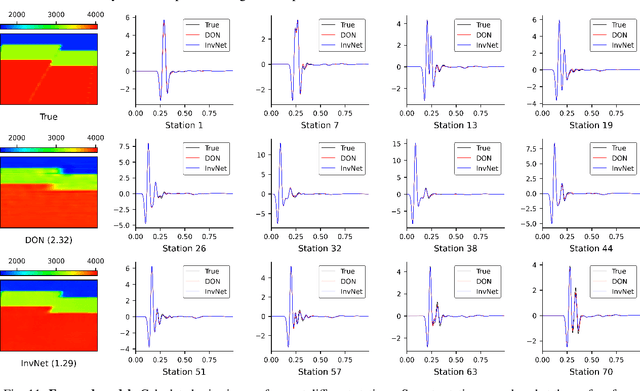
Full Waveform Inversion (FWI) is an important geophysical technique considered in subsurface property prediction. It solves the inverse problem of predicting high-resolution Earth interior models from seismic data. Traditional FWI methods are computationally demanding. Inverse problems in geophysics often face challenges of non-uniqueness due to limited data, as data are often collected only on the surface. In this study, we introduce a novel methodology that leverages Deep Operator Networks (DeepONet) to attempt to improve both the efficiency and accuracy of FWI. The proposed DeepONet methodology inverts seismic waveforms for the subsurface velocity field. This approach is able to capture some key features of the subsurface velocity field. We have shown that the architecture can be applied to noisy seismic data with an accuracy that is better than some other machine learning methods. We also test our proposed method with out-of-distribution prediction for different velocity models. The proposed DeepONet shows comparable and better accuracy in some velocity models than some other machine learning methods. To improve the FWI workflow, we propose using the DeepONet output as a starting model for conventional FWI and that it may improve FWI performance. While we have only shown that DeepONet facilitates faster convergence than starting with a homogeneous velocity field, it may have some benefits compared to other approaches to constructing starting models. This integration of DeepONet into FWI may accelerate the inversion process and may also enhance its robustness and reliability.

Representation Meets Optimization: Training PINNs and PIKANs for Gray-Box Discovery in Systems Pharmacology

Physics-Informed Kolmogorov-Arnold Networks (PIKANs) are gaining attention as an effective counterpart to the original multilayer perceptron-based Physics-Informed Neural Networks (PINNs). Both representation models can address inverse problems and facilitate gray-box system identification. However, a comprehensive understanding of their performance in terms of accuracy and speed remains underexplored. In particular, we introduce a modified PIKAN architecture, tanh-cPIKAN, which is based on Chebyshev polynomials for parametrization of the univariate functions with an extra nonlinearity for enhanced performance. We then present a systematic investigation of how choices of the optimizer, representation, and training configuration influence the performance of PINNs and PIKANs in the context of systems pharmacology modeling. We benchmark a wide range of first-order, second-order, and hybrid optimizers, including various learning rate schedulers. We use the new Optax library to identify the most effective combinations for learning gray-boxes under ill-posed, non-unique, and data-sparse conditions. We examine the influence of model architecture (MLP vs. KAN), numerical precision (single vs. double), the need for warm-up phases for second-order methods, and sensitivity to the initial learning rate. We also assess the optimizer scalability for larger models and analyze the trade-offs introduced by JAX in terms of computational efficiency and numerical accuracy. Using two representative systems pharmacology case studies - a pharmacokinetics model and a chemotherapy drug-response model - we offer practical guidance on selecting optimizers and representation models/architectures for robust and efficient gray-box discovery. Our findings provide actionable insights for improving the training of physics-informed networks in biomedical applications and beyond.

Discovering Partially Known Ordinary Differential Equations: a Case Study on the Chemical Kinetics of Cellulose Degradation

The degree of polymerization (DP) is one of the methods for estimating the aging of the polymer based insulation systems, such as cellulose insulation in power components. The main degradation mechanisms in polymers are hydrolysis, pyrolysis, and oxidation. These mechanisms combined cause a reduction of the DP. However, the data availability for these types of problems is usually scarce. This study analyzes insulation aging using cellulose degradation data from power transformers. The aging problem for the cellulose immersed in mineral oil inside power transformers is modeled with ordinary differential equations (ODEs). We recover the governing equations of the degradation system using Physics-Informed Neural Networks (PINNs) and symbolic regression. We apply PINNs to discover the Arrhenius equation's unknown parameters in the Ekenstam ODE describing cellulose contamination content and the material aging process related to temperature for synthetic data and real DP values. A modification of the Ekenstam ODE is given by Emsley's system of ODEs, where the rate constant expressed by the Arrhenius equation decreases in time with the new formulation. We use PINNs and symbolic regression to recover the functional form of one of the ODEs of the system and to identify an unknown parameter.

A Neural Operator-Based Emulator for Regional Shallow Water Dynamics

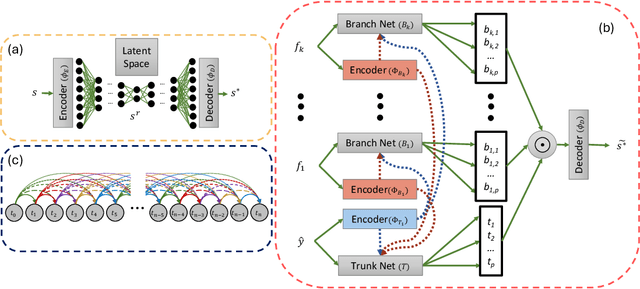
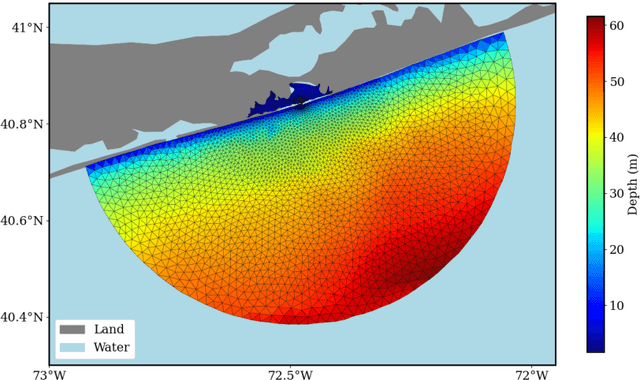
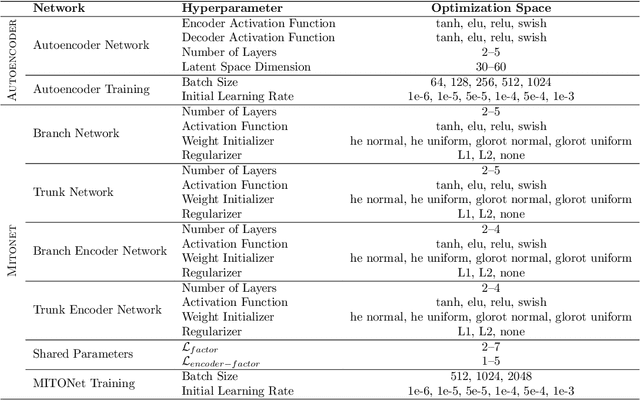
Coastal regions are particularly vulnerable to the impacts of rising sea levels and extreme weather events. Accurate real-time forecasting of hydrodynamic processes in these areas is essential for infrastructure planning and climate adaptation. In this study, we present the Multiple-Input Temporal Operator Network (MITONet), a novel autoregressive neural emulator that employs dimensionality reduction to efficiently approximate high-dimensional numerical solvers for complex, nonlinear problems that are governed by time-dependent, parameterized partial differential equations. Although MITONet is applicable to a wide range of problems, we showcase its capabilities by forecasting regional tide-driven dynamics described by the two-dimensional shallow-water equations, while incorporating initial conditions, boundary conditions, and a varying domain parameter. We demonstrate MITONet's performance in a real-world application, highlighting its ability to make accurate predictions by extrapolating both in time and parametric space.

NeuroSEM: A hybrid framework for simulating multiphysics problems by coupling PINNs and spectral elements

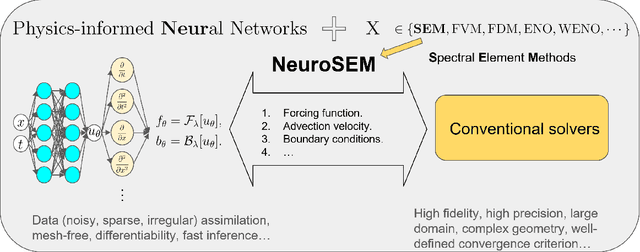
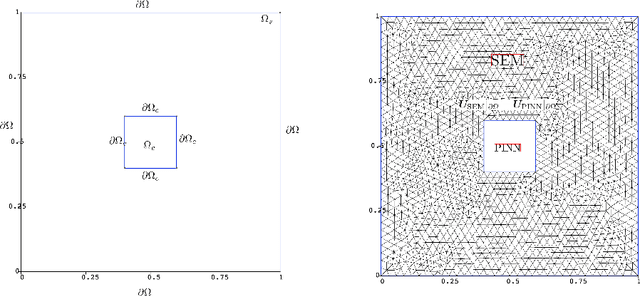
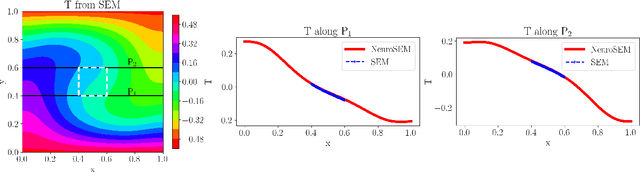
Multiphysics problems that are characterized by complex interactions among fluid dynamics, heat transfer, structural mechanics, and electromagnetics, are inherently challenging due to their coupled nature. While experimental data on certain state variables may be available, integrating these data with numerical solvers remains a significant challenge. Physics-informed neural networks (PINNs) have shown promising results in various engineering disciplines, particularly in handling noisy data and solving inverse problems. However, their effectiveness in forecasting nonlinear phenomena in multiphysics regimes is yet to be fully established. This study introduces NeuroSEM, a hybrid framework integrating PINNs with the high-fidelity Spectral Element Method (SEM) solver, Nektar++. NeuroSEM leverages strengths of both PINNs and SEM, providing robust solutions for multiphysics problems. PINNs are trained to assimilate data and model physical phenomena in specific subdomains, which are then integrated into Nektar++. We demonstrate the efficiency and accuracy of NeuroSEM for thermal convection in cavity flow and flow past a cylinder. The framework effectively handles data assimilation by addressing those subdomains and state variables where data are available. We applied NeuroSEM to the Rayleigh-B\'enard convection system, including cases with missing thermal boundary conditions. Our results indicate that NeuroSEM accurately models the physical phenomena and assimilates the data within the specified subdomains. The framework's plug-and-play nature facilitates its extension to other multiphysics or multiscale problems. Furthermore, NeuroSEM is optimized for an efficient execution on emerging integrated GPU-CPU architectures. This hybrid approach enhances the accuracy and efficiency of simulations, making it a powerful tool for tackling complex engineering challenges in various scientific domains.

A comprehensive and FAIR comparison between MLP and KAN representations for differential equations and operator networks

Kolmogorov-Arnold Networks (KANs) were recently introduced as an alternative representation model to MLP. Herein, we employ KANs to construct physics-informed machine learning models (PIKANs) and deep operator models (DeepOKANs) for solving differential equations for forward and inverse problems. In particular, we compare them with physics-informed neural networks (PINNs) and deep operator networks (DeepONets), which are based on the standard MLP representation. We find that although the original KANs based on the B-splines parameterization lack accuracy and efficiency, modified versions based on low-order orthogonal polynomials have comparable performance to PINNs and DeepONet although they still lack robustness as they may diverge for different random seeds or higher order orthogonal polynomials. We visualize their corresponding loss landscapes and analyze their learning dynamics using information bottleneck theory. Our study follows the FAIR principles so that other researchers can use our benchmarks to further advance this emerging topic.

Rethinking materials simulations: Blending direct numerical simulations with neural operators

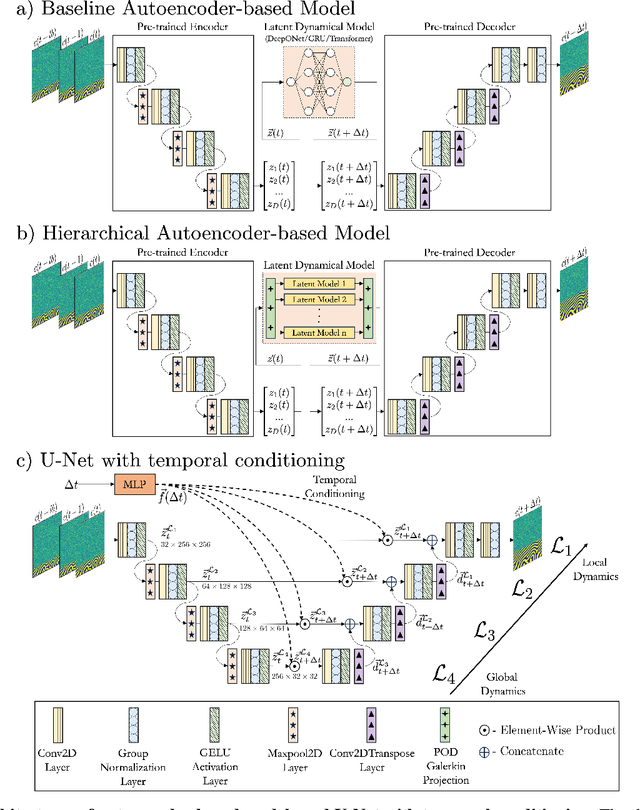
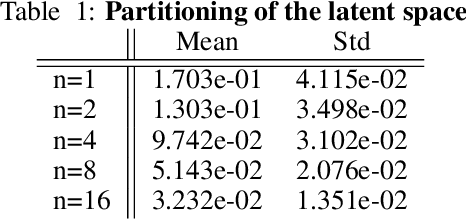
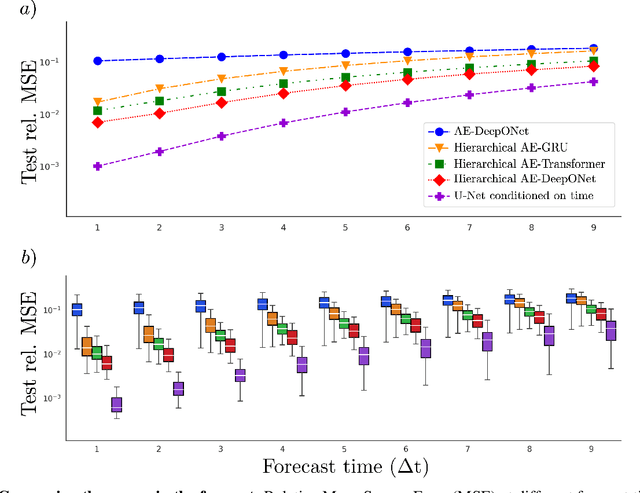
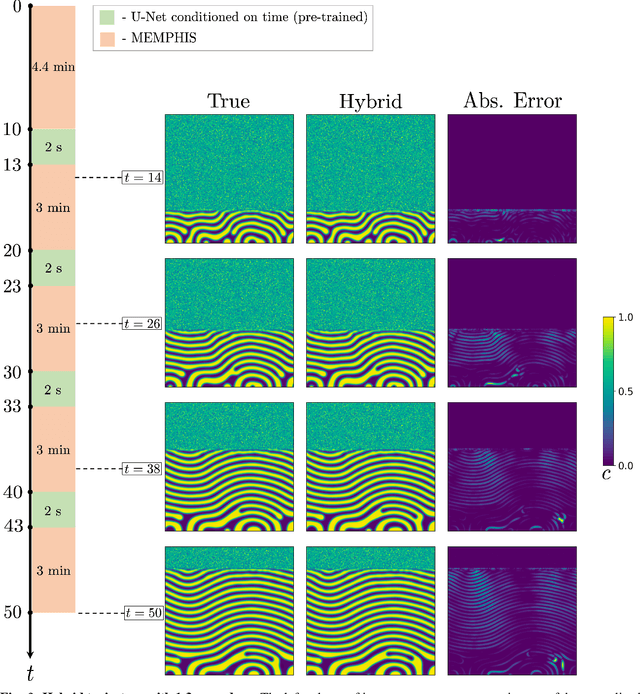
Direct numerical simulations (DNS) are accurate but computationally expensive for predicting materials evolution across timescales, due to the complexity of the underlying evolution equations, the nature of multiscale spatio-temporal interactions, and the need to reach long-time integration. We develop a new method that blends numerical solvers with neural operators to accelerate such simulations. This methodology is based on the integration of a community numerical solver with a U-Net neural operator, enhanced by a temporal-conditioning mechanism that enables accurate extrapolation and efficient time-to-solution predictions of the dynamics. We demonstrate the effectiveness of this framework on simulations of microstructure evolution during physical vapor deposition modeled via the phase-field method. Such simulations exhibit high spatial gradients due to the co-evolution of different material phases with simultaneous slow and fast materials dynamics. We establish accurate extrapolation of the coupled solver with up to 16.5$\times$ speed-up compared to DNS. This methodology is generalizable to a broad range of evolutionary models, from solid mechanics, to fluid dynamics, geophysics, climate, and more.

Randomized Forward Mode of Automatic Differentiation for Optimization Algorithms

Backpropagation within neural networks leverages a fundamental element of automatic differentiation, which is referred to as the reverse mode differentiation, or vector Jacobian Product (VJP) or, in the context of differential geometry, known as the pull-back process. The computation of gradient is important as update of neural network parameters is performed using gradient descent method. In this study, we present a genric randomized method, which updates the parameters of neural networks by using directional derivatives of loss functions computed efficiently by using forward mode AD or Jacobian vector Product (JVP). These JVP are computed along the random directions sampled from different probability distributions e.g., Bernoulli, Normal, Wigner, Laplace and Uniform distributions. The computation of gradient is performed during the forward pass of the neural network. We also present a rigorous analysis of the presented methods providing the rate of convergence along with the computational experiments deployed in scientific Machine learning in particular physics-informed neural networks and Deep Operator Networks.