A Neural Operator-Based Emulator for Regional Shallow Water Dynamics

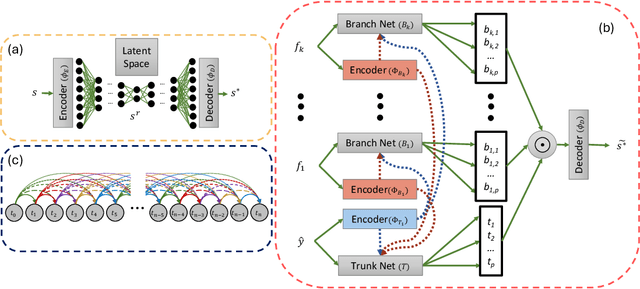
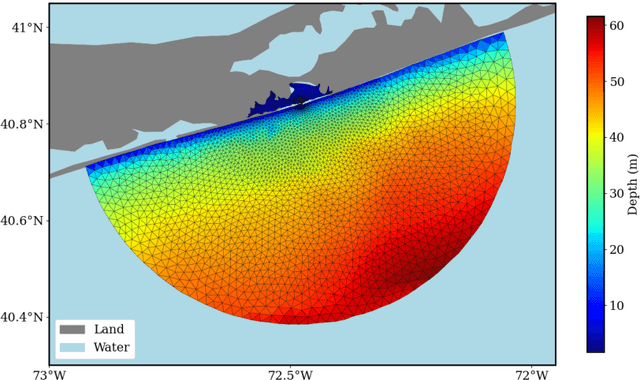
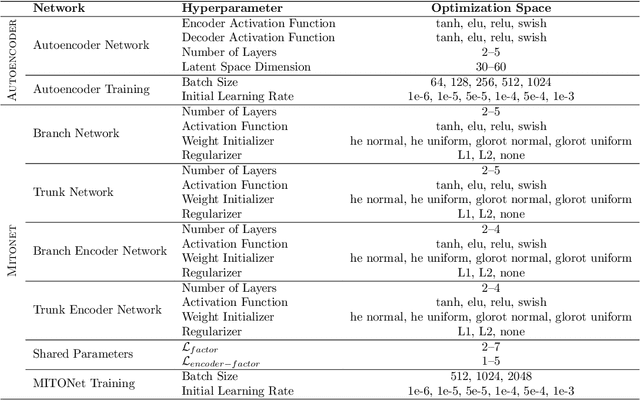
Coastal regions are particularly vulnerable to the impacts of rising sea levels and extreme weather events. Accurate real-time forecasting of hydrodynamic processes in these areas is essential for infrastructure planning and climate adaptation. In this study, we present the Multiple-Input Temporal Operator Network (MITONet), a novel autoregressive neural emulator that employs dimensionality reduction to efficiently approximate high-dimensional numerical solvers for complex, nonlinear problems that are governed by time-dependent, parameterized partial differential equations. Although MITONet is applicable to a wide range of problems, we showcase its capabilities by forecasting regional tide-driven dynamics described by the two-dimensional shallow-water equations, while incorporating initial conditions, boundary conditions, and a varying domain parameter. We demonstrate MITONet's performance in a real-world application, highlighting its ability to make accurate predictions by extrapolating both in time and parametric space.

Data-driven reduced order modeling of environmental hydrodynamics using deep autoencoders and neural ODEs

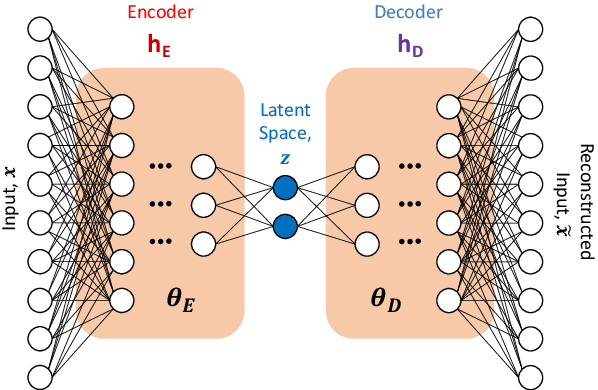
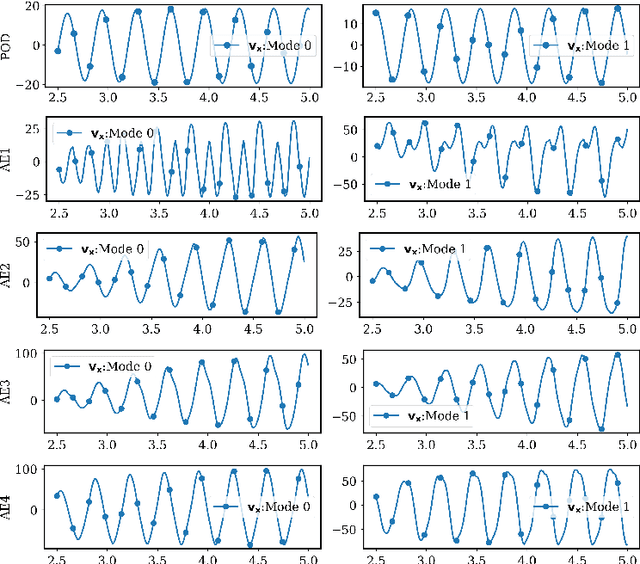
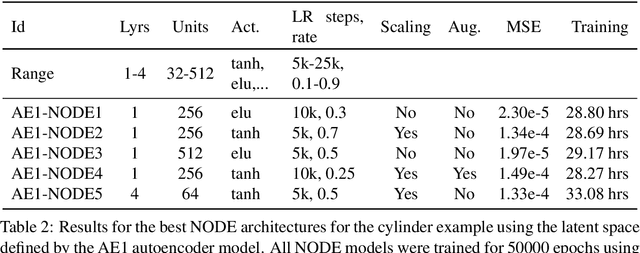
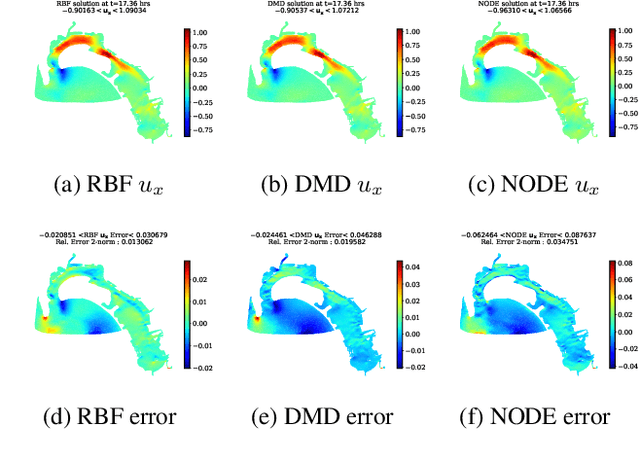
Model reduction for fluid flow simulation continues to be of great interest across a number of scientific and engineering fields. In a previous work [arXiv:2104.13962], we explored the use of Neural Ordinary Differential Equations (NODE) as a non-intrusive method for propagating the latent-space dynamics in reduced order models. Here, we investigate employing deep autoencoders for discovering the reduced basis representation, the dynamics of which are then approximated by NODE. The ability of deep autoencoders to represent the latent-space is compared to the traditional proper orthogonal decomposition (POD) approach, again in conjunction with NODE for capturing the dynamics. Additionally, we compare their behavior with two classical non-intrusive methods based on POD and radial basis function interpolation as well as dynamic mode decomposition. The test problems we consider include incompressible flow around a cylinder as well as a real-world application of shallow water hydrodynamics in an estuarine system. Our findings indicate that deep autoencoders can leverage nonlinear manifold learning to achieve a highly efficient compression of spatial information and define a latent-space that appears to be more suitable for capturing the temporal dynamics through the NODE framework.

Neural Ordinary Differential Equations for Data-Driven Reduced Order Modeling of Environmental Hydrodynamics

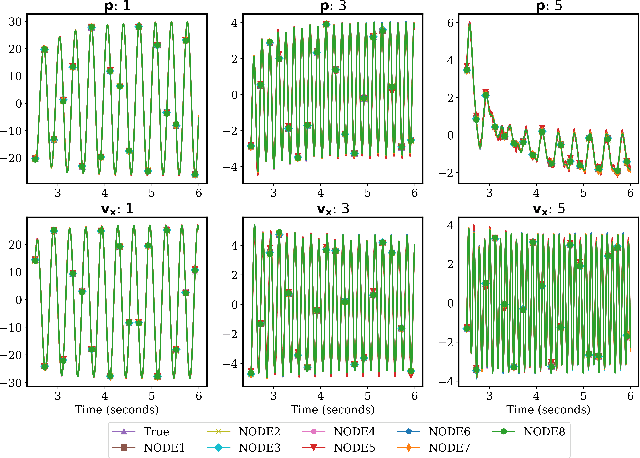
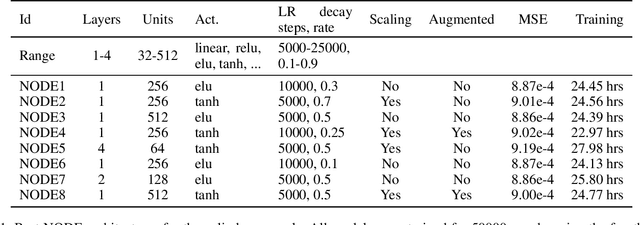
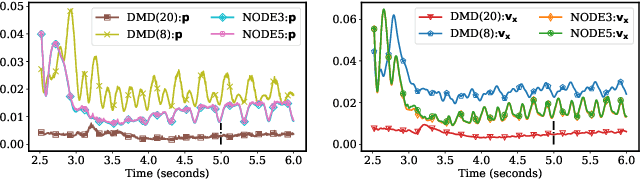
Model reduction for fluid flow simulation continues to be of great interest across a number of scientific and engineering fields. Here, we explore the use of Neural Ordinary Differential Equations, a recently introduced family of continuous-depth, differentiable networks (Chen et al 2018), as a way to propagate latent-space dynamics in reduced order models. We compare their behavior with two classical non-intrusive methods based on proper orthogonal decomposition and radial basis function interpolation as well as dynamic mode decomposition. The test problems we consider include incompressible flow around a cylinder as well as real-world applications of shallow water hydrodynamics in riverine and estuarine systems. Our findings indicate that Neural ODEs provide an elegant framework for stable and accurate evolution of latent-space dynamics with a promising potential of extrapolatory predictions. However, in order to facilitate their widespread adoption for large-scale systems, significant effort needs to be directed at accelerating their training times. This will enable a more comprehensive exploration of the hyperparameter space for building generalizable Neural ODE approximations over a wide range of system dynamics.