Forecasting Geoffective Events from Solar Wind Data and Evaluating the Most Predictive Features through Machine Learning Approaches

This study addresses the prediction of geomagnetic disturbances by exploiting machine learning techniques. Specifically, the Long-Short Term Memory recurrent neural network, which is particularly suited for application over long time series, is employed in the analysis of in-situ measurements of solar wind plasma and magnetic field acquired over more than one solar cycle, from $2005$ to $2019$, at the Lagrangian point L$1$. The problem is approached as a binary classification aiming to predict one hour in advance a decrease in the SYM-H geomagnetic activity index below the threshold of $-50$ nT, which is generally regarded as indicative of magnetospheric perturbations. The strong class imbalance issue is tackled by using an appropriate loss function tailored to optimize appropriate skill scores in the training phase of the neural network. Beside classical skill scores, value-weighted skill scores are then employed to evaluate predictions, suitable in the study of problems, such as the one faced here, characterized by strong temporal variability. For the first time, the content of magnetic helicity and energy carried by solar transients, associated with their detection and likelihood of geo-effectiveness, were considered as input features of the network architecture. Their predictive capabilities are demonstrated through a correlation-driven feature selection method to rank the most relevant characteristics involved in the neural network prediction model. The optimal performance of the adopted neural network in properly forecasting the onset of geomagnetic storms, which is a crucial point for giving real warnings in an operational setting, is finally showed.

Greedy feature selection: Classifier-dependent feature selection via greedy methods

The purpose of this study is to introduce a new approach to feature ranking for classification tasks, called in what follows greedy feature selection. In statistical learning, feature selection is usually realized by means of methods that are independent of the classifier applied to perform the prediction using that reduced number of features. Instead, greedy feature selection identifies the most important feature at each step and according to the selected classifier. In the paper, the benefits of such scheme are investigated theoretically in terms of model capacity indicators, such as the Vapnik-Chervonenkis (VC) dimension or the kernel alignment, and tested numerically by considering its application to the problem of predicting geo-effective manifestations of the active Sun.

AI-FLARES: Artificial Intelligence for the Analysis of Solar Flares Data

AI-FLARES (Artificial Intelligence for the Analysis of Solar Flares Data) is a research project funded by the Agenzia Spaziale Italiana and by the Istituto Nazionale di Astrofisica within the framework of the ``Attivit\`a di Studio per la Comunit\`a Scientifica Nazionale Sole, Sistema Solare ed Esopianeti'' program. The topic addressed by this project was the development and use of computational methods for the analysis of remote sensing space data associated to solar flare emission. This paper overviews the main results obtained by the project, with specific focus on solar flare forecasting, reconstruction of morphologies of the flaring sources, and interpretation of acceleration mechanisms triggered by solar flares.

Interpolation with the polynomial kernels

The polynomial kernels are widely used in machine learning and they are one of the default choices to develop kernel-based classification and regression models. However, they are rarely used and considered in numerical analysis due to their lack of strict positive definiteness. In particular they do not enjoy the usual property of unisolvency for arbitrary point sets, which is one of the key properties used to build kernel-based interpolation methods. This paper is devoted to establish some initial results for the study of these kernels, and their related interpolation algorithms, in the context of approximation theory. We will first prove necessary and sufficient conditions on point sets which guarantee the existence and uniqueness of an interpolant. We will then study the Reproducing Kernel Hilbert Spaces (or native spaces) of these kernels and their norms, and provide inclusion relations between spaces corresponding to different kernel parameters. With these spaces at hand, it will be further possible to derive generic error estimates which apply to sufficiently smooth functions, thus escaping the native space. Finally, we will show how to employ an efficient stable algorithm to these kernels to obtain accurate interpolants, and we will test them in some numerical experiment. After this analysis several computational and theoretical aspects remain open, and we will outline possible further research directions in a concluding section. This work builds some bridges between kernel and polynomial interpolation, two topics to which the authors, to different extents, have been introduced under the supervision or through the work of Stefano De Marchi. For this reason, they wish to dedicate this work to him in the occasion of his 60th birthday.

Data-driven reduced order modeling of environmental hydrodynamics using deep autoencoders and neural ODEs

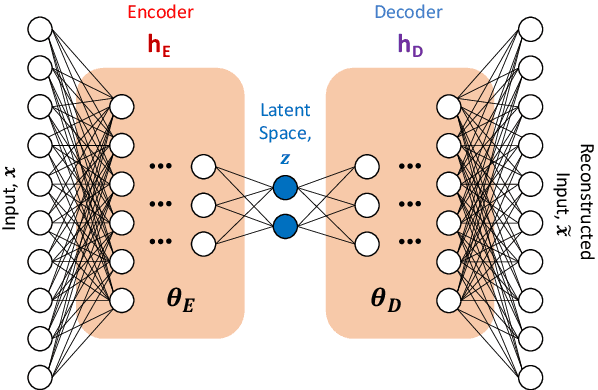
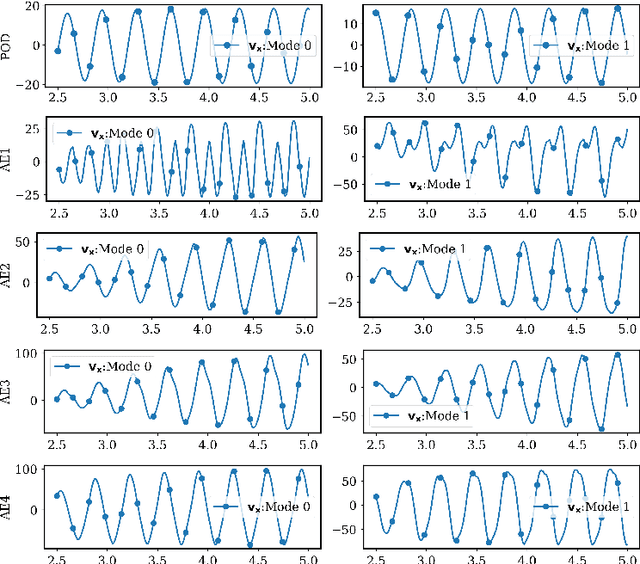
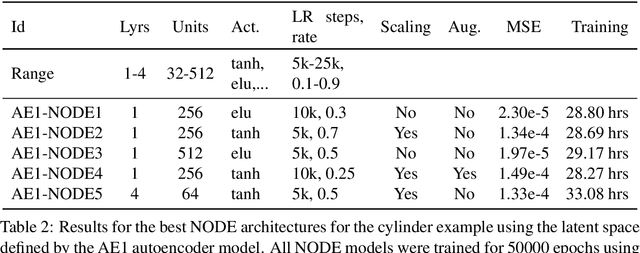
Model reduction for fluid flow simulation continues to be of great interest across a number of scientific and engineering fields. In a previous work [arXiv:2104.13962], we explored the use of Neural Ordinary Differential Equations (NODE) as a non-intrusive method for propagating the latent-space dynamics in reduced order models. Here, we investigate employing deep autoencoders for discovering the reduced basis representation, the dynamics of which are then approximated by NODE. The ability of deep autoencoders to represent the latent-space is compared to the traditional proper orthogonal decomposition (POD) approach, again in conjunction with NODE for capturing the dynamics. Additionally, we compare their behavior with two classical non-intrusive methods based on POD and radial basis function interpolation as well as dynamic mode decomposition. The test problems we consider include incompressible flow around a cylinder as well as a real-world application of shallow water hydrodynamics in an estuarine system. Our findings indicate that deep autoencoders can leverage nonlinear manifold learning to achieve a highly efficient compression of spatial information and define a latent-space that appears to be more suitable for capturing the temporal dynamics through the NODE framework.

Visibility Interpolation in Solar Hard X-ray Imaging: Application to RHESSI and STIX

Space telescopes for solar hard X-ray imaging provide observations made of sampled Fourier components of the incoming photon flux. The aim of this study is to design an image reconstruction method relying on enhanced visibility interpolation in the Fourier domain. % methods heading (mandatory) The interpolation-based method is applied on synthetic visibilities generated by means of the simulation software implemented within the framework of the Spectrometer/Telescope for Imaging X-rays (STIX) mission on board Solar Orbiter. An application to experimental visibilities observed by the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI) is also considered. In order to interpolate these visibility data we have utilized an approach based on Variably Scaled Kernels (VSKs), which are able to realize feature augmentation by exploiting prior information on the flaring source and which are used here, for the first time, for image reconstruction purposes.} % results heading (mandatory) When compared to an interpolation-based reconstruction algorithm previously introduced for RHESSI, VSKs offer significantly better performances, particularly in the case of STIX imaging, which is characterized by a notably sparse sampling of the Fourier domain. In the case of RHESSI data, this novel approach is particularly reliable when either the flaring sources are characterized by narrow, ribbon-like shapes or high-resolution detectors are utilized for observations. % conclusions heading (optional), leave it empty if necessary The use of VSKs for interpolating hard X-ray visibilities allows a notable image reconstruction accuracy when the information on the flaring source is encoded by a small set of scattered Fourier data and when the visibility surface is affected by significant oscillations in the frequency domain.