Interpolation with the polynomial kernels

The polynomial kernels are widely used in machine learning and they are one of the default choices to develop kernel-based classification and regression models. However, they are rarely used and considered in numerical analysis due to their lack of strict positive definiteness. In particular they do not enjoy the usual property of unisolvency for arbitrary point sets, which is one of the key properties used to build kernel-based interpolation methods. This paper is devoted to establish some initial results for the study of these kernels, and their related interpolation algorithms, in the context of approximation theory. We will first prove necessary and sufficient conditions on point sets which guarantee the existence and uniqueness of an interpolant. We will then study the Reproducing Kernel Hilbert Spaces (or native spaces) of these kernels and their norms, and provide inclusion relations between spaces corresponding to different kernel parameters. With these spaces at hand, it will be further possible to derive generic error estimates which apply to sufficiently smooth functions, thus escaping the native space. Finally, we will show how to employ an efficient stable algorithm to these kernels to obtain accurate interpolants, and we will test them in some numerical experiment. After this analysis several computational and theoretical aspects remain open, and we will outline possible further research directions in a concluding section. This work builds some bridges between kernel and polynomial interpolation, two topics to which the authors, to different extents, have been introduced under the supervision or through the work of Stefano De Marchi. For this reason, they wish to dedicate this work to him in the occasion of his 60th birthday.

Graph Wedgelets: Adaptive Data Compression on Graphs based on Binary Wedge Partitioning Trees and Geometric Wavelets

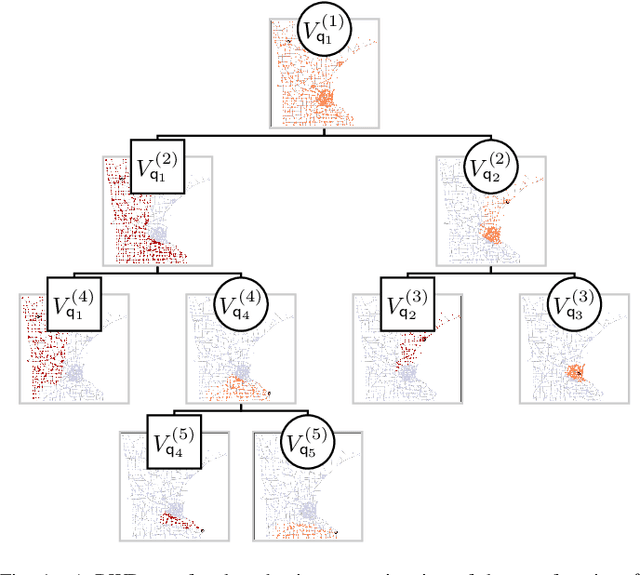
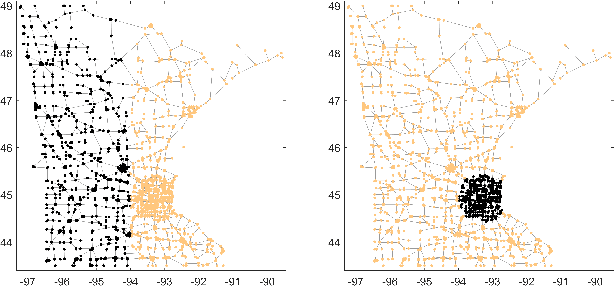
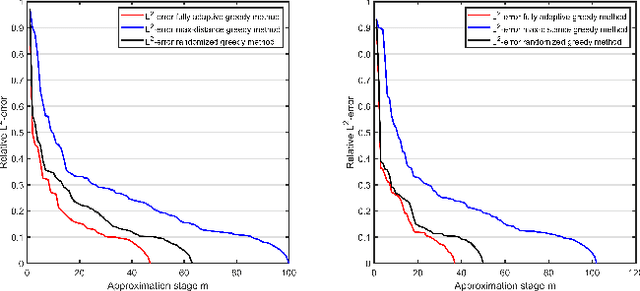
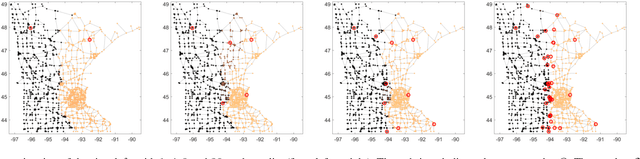
We introduce graph wedgelets - a tool for data compression on graphs based on the representation of signals by piecewise constant functions on adaptively generated binary wedge partitionings of a graph. For this, we transfer partitioning and compression techniques known for 2D images to general graph structures and develop discrete variants of continuous wedgelets and binary space partitionings. We prove that continuous results on best $m$-term approximation with geometric wavelets can be transferred to the discrete graph setting and show that our wedgelet representation of graph signals can be encoded and implemented in a simple way. Finally, we illustrate that this graph-based method can be applied for the compression of images as well.

Simple Graph Convolutional Networks

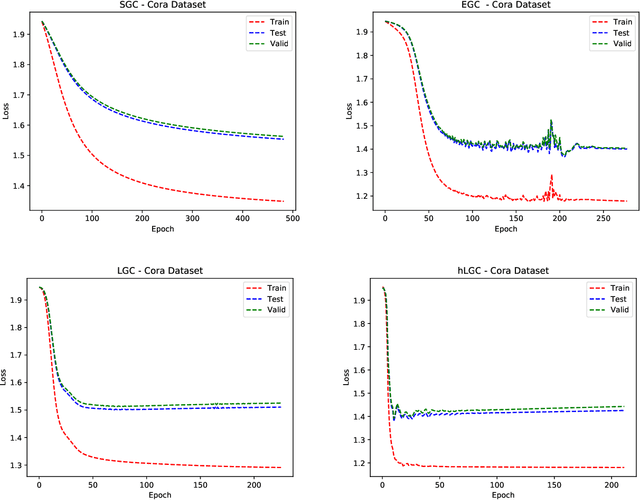
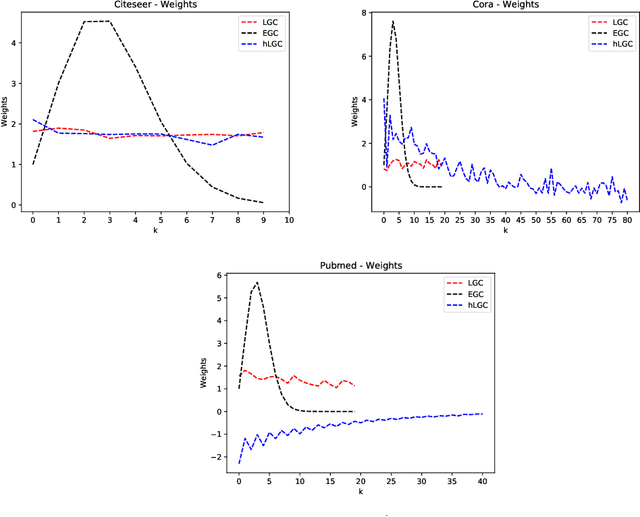
Many neural networks for graphs are based on the graph convolution operator, proposed more than a decade ago. Since then, many alternative definitions have been proposed, that tend to add complexity (and non-linearity) to the model. In this paper, we follow the opposite direction by proposing simple graph convolution operators, that can be implemented in single-layer graph convolutional networks. We show that our convolution operators are more theoretically grounded than many proposals in literature, and exhibit state-of-the-art predictive performance on the considered benchmark datasets.

Kernel-Based Models for Influence Maximization on Graphs based on Gaussian Process Variance Minimization

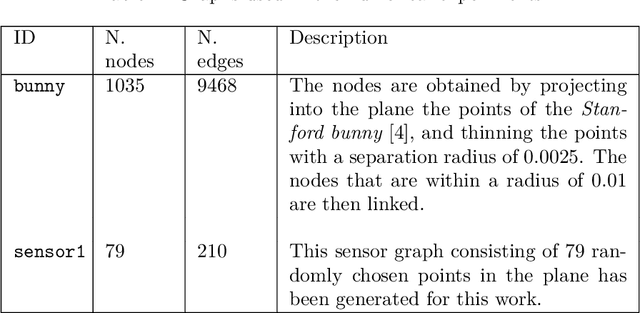
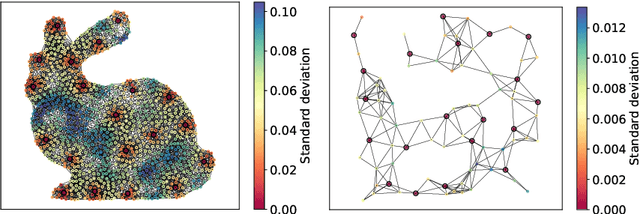
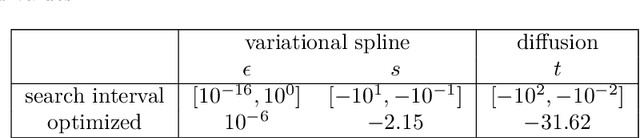
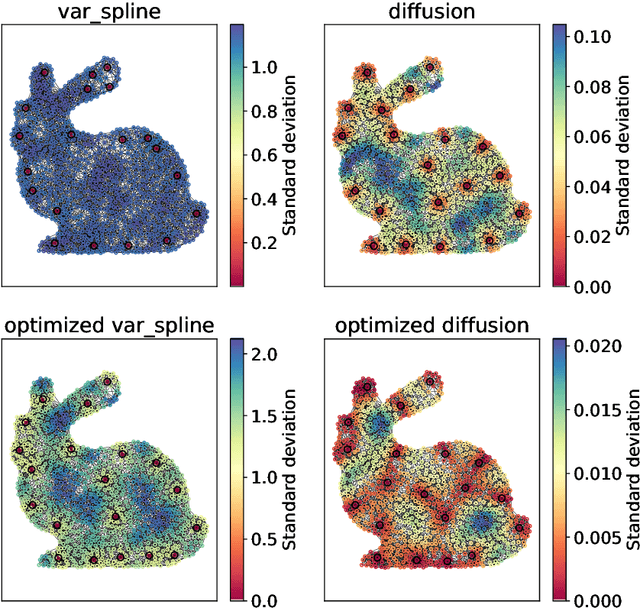
The inference of novel knowledge, the discovery of hidden patterns, and the uncovering of insights from large amounts of data from a multitude of sources make Data Science (DS) to an art rather than just a mere scientific discipline. The study and design of mathematical models able to analyze information represents a central research topic in DS. In this work, we introduce and investigate a novel model for influence maximization (IM) on graphs using ideas from kernel-based approximation, Gaussian process regression, and the minimization of a corresponding variance term. Data-driven approaches can be applied to determine proper kernels for this IM model and machine learning methodologies are adopted to tune the model parameters. Compared to stochastic models in this field that rely on costly Monte-Carlo simulations, our model allows for a simple and cost-efficient update strategy to compute optimal influencing nodes on a graph. In several numerical experiments, we show the properties and benefits of this new model.

Semi-Supervised Learning on Graphs with Feature-Augmented Graph Basis Functions

For semi-supervised learning on graphs, we study how initial kernels in a supervised learning regime can be augmented with additional information from known priors or from unsupervised learning outputs. These augmented kernels are constructed in a simple update scheme based on the Schur-Hadamard product of the kernel with additional feature kernels. As generators of the positive definite kernels we will focus on graph basis functions (GBF) that allow to include geometric information of the graph via the graph Fourier transform. Using a regularized least squares (RLS) approach for machine learning, we will test the derived augmented kernels for the classification of data on graphs.