Kernel-Based Models for Influence Maximization on Graphs based on Gaussian Process Variance Minimization

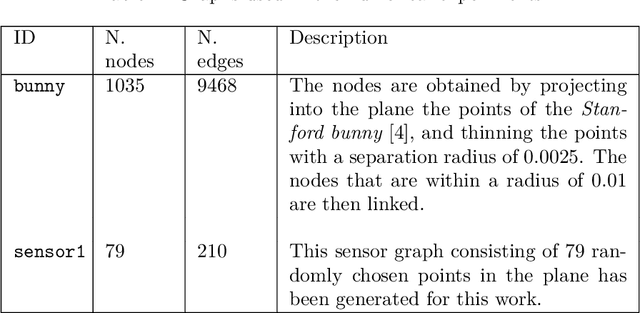
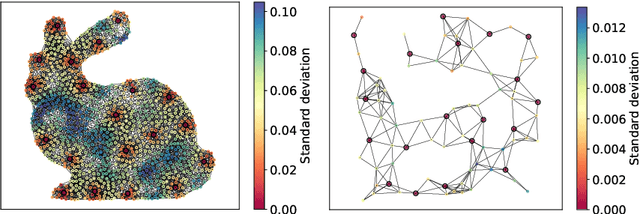
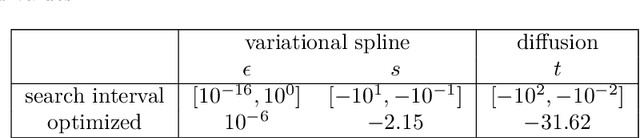
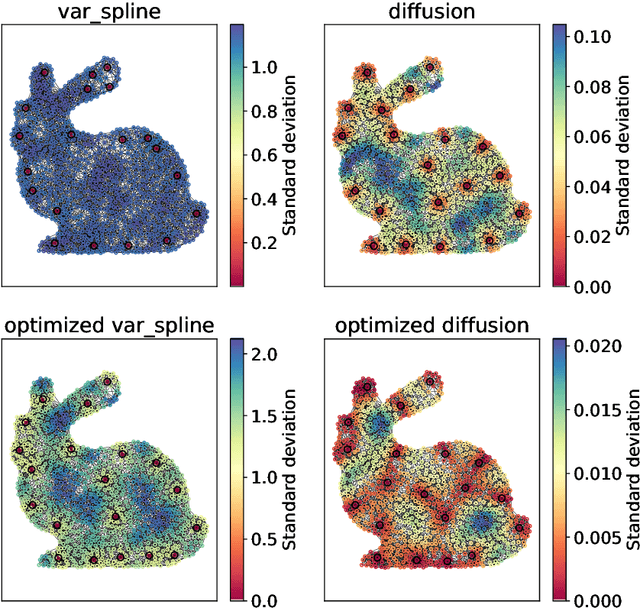
The inference of novel knowledge, the discovery of hidden patterns, and the uncovering of insights from large amounts of data from a multitude of sources make Data Science (DS) to an art rather than just a mere scientific discipline. The study and design of mathematical models able to analyze information represents a central research topic in DS. In this work, we introduce and investigate a novel model for influence maximization (IM) on graphs using ideas from kernel-based approximation, Gaussian process regression, and the minimization of a corresponding variance term. Data-driven approaches can be applied to determine proper kernels for this IM model and machine learning methodologies are adopted to tune the model parameters. Compared to stochastic models in this field that rely on costly Monte-Carlo simulations, our model allows for a simple and cost-efficient update strategy to compute optimal influencing nodes on a graph. In several numerical experiments, we show the properties and benefits of this new model.