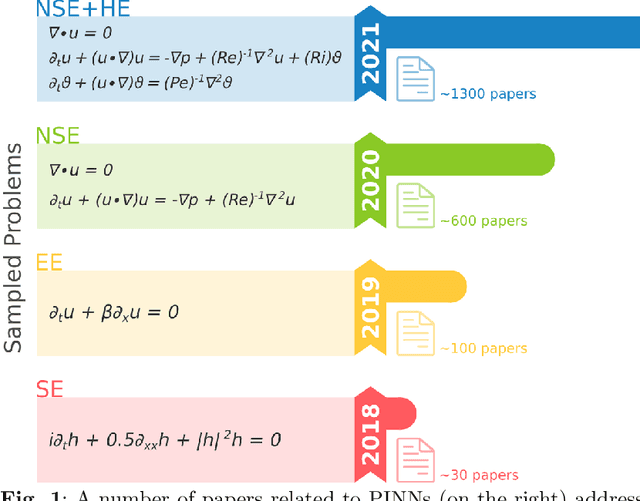
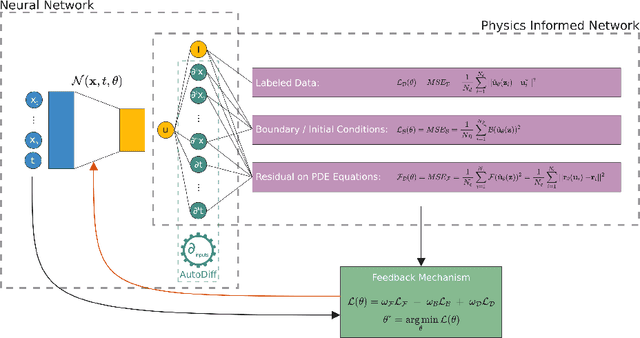
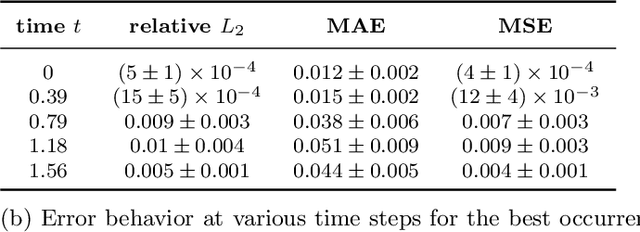
Scientific Machine Learning through Physics-Informed Neural Networks: Where we are and What's next

Physics-Informed Neural Networks (PINN) are neural networks (NNs) that encode model equations, like Partial Differential Equations (PDE), as a component of the neural network itself. PINNs are nowadays used to solve PDEs, fractional equations, and integral-differential equations. This novel methodology has arisen as a multi-task learning framework in which a NN must fit observed data while reducing a PDE residual. This article provides a comprehensive review of the literature on PINNs: while the primary goal of the study was to characterize these networks and their related advantages and disadvantages, the review also attempts to incorporate publications on a larger variety of issues, including physics-constrained neural networks (PCNN), where the initial or boundary conditions are directly embedded in the NN structure rather than in the loss functions. The study indicates that most research has focused on customizing the PINN through different activation functions, gradient optimization techniques, neural network structures, and loss function structures. Despite the wide range of applications for which PINNs have been used, by demonstrating their ability to be more feasible in some contexts than classical numerical techniques like Finite Element Method (FEM), advancements are still possible, most notably theoretical issues that remain unresolved.

Heterogeneous Data Fusion Considering Spatial Correlations using Graph Convolutional Networks and its Application in Air Quality Prediction

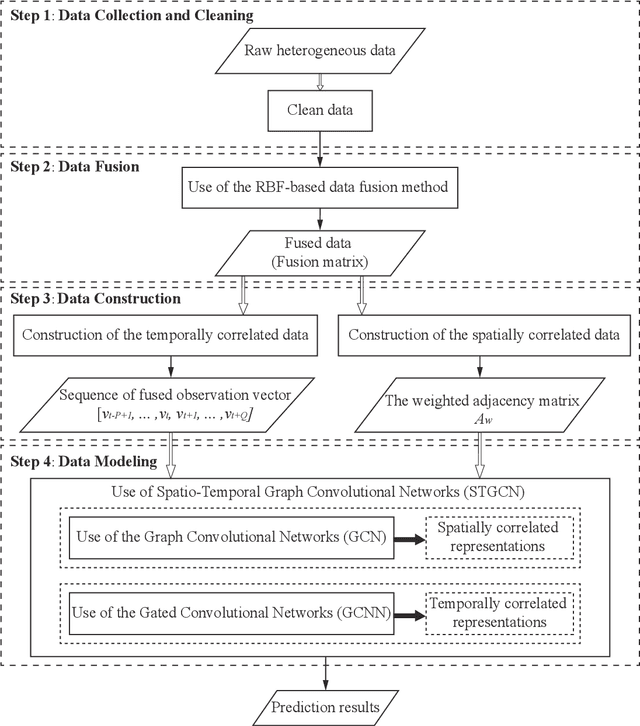
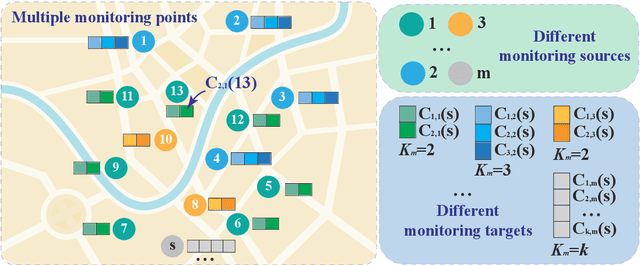
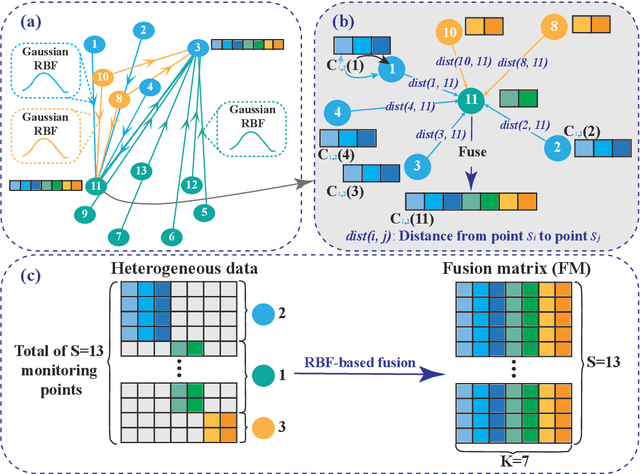
Heterogeneous data are commonly adopted as the inputs for some models that predict the future trends of some observations. Existing predictive models typically ignore the inconsistencies and imperfections in heterogeneous data while also failing to consider the (1) spatial correlations among monitoring points or (2) predictions for the entire study area. To address the above problems, this paper proposes a deep learning method for fusing heterogeneous data collected from multiple monitoring points using graph convolutional networks (GCNs) to predict the future trends of some observations and evaluates its effectiveness by applying it in an air quality predictions scenario. The essential idea behind the proposed method is to (1) fuse the collected heterogeneous data based on the locations of the monitoring points with regard to their spatial correlations and (2) perform prediction based on global information rather than local information. In the proposed method, first, we assemble a fusion matrix using the proposed RBF-based fusion approach; second, based on the fused data, we construct spatially and temporally correlated data as inputs for the predictive model; finally, we employ the spatiotemporal graph convolutional network (STGCN) to predict the future trends of some observations. In the application scenario of air quality prediction, it is observed that (1) the fused data derived from the RBF-based fusion approach achieve satisfactory consistency; (2) the performances of the prediction models based on fused data are better than those based on raw data; and (3) the STGCN model achieves the best performance when compared to those of all baseline models. The proposed method is applicable for similar scenarios where continuous heterogeneous data are collected from multiple monitoring points scattered across a study area.

Kernel-Based Models for Influence Maximization on Graphs based on Gaussian Process Variance Minimization

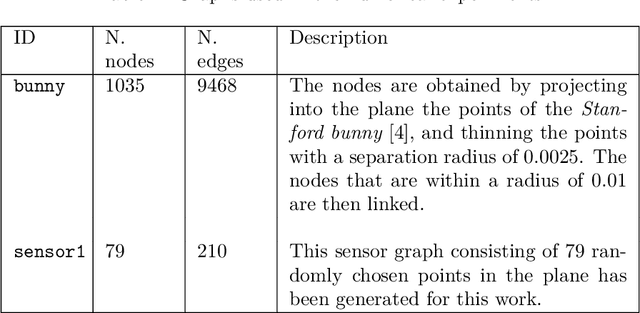
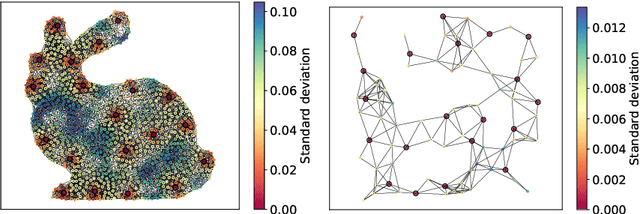
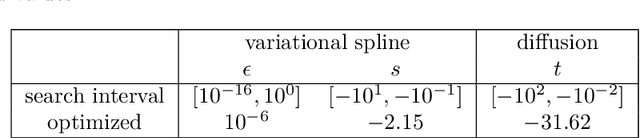
The inference of novel knowledge, the discovery of hidden patterns, and the uncovering of insights from large amounts of data from a multitude of sources make Data Science (DS) to an art rather than just a mere scientific discipline. The study and design of mathematical models able to analyze information represents a central research topic in DS. In this work, we introduce and investigate a novel model for influence maximization (IM) on graphs using ideas from kernel-based approximation, Gaussian process regression, and the minimization of a corresponding variance term. Data-driven approaches can be applied to determine proper kernels for this IM model and machine learning methodologies are adopted to tune the model parameters. Compared to stochastic models in this field that rely on costly Monte-Carlo simulations, our model allows for a simple and cost-efficient update strategy to compute optimal influencing nodes on a graph. In several numerical experiments, we show the properties and benefits of this new model.

Julia Language in Machine Learning: Algorithms, Applications, and Open Issues

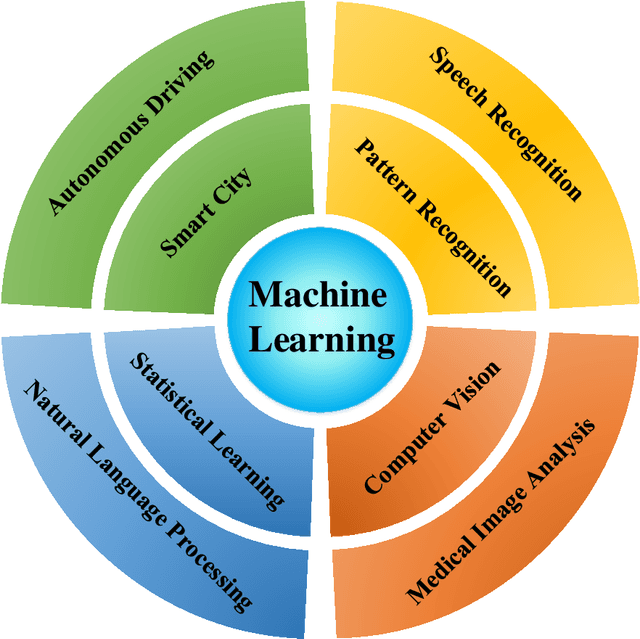
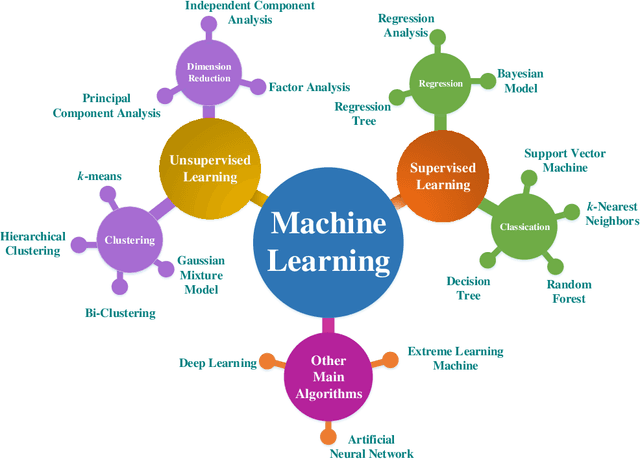
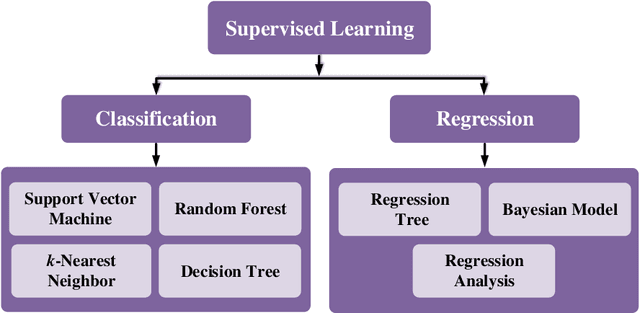
Machine learning is driving development across many fields in science and engineering. A simple and efficient programming language could accelerate applications of machine learning in various fields. Currently, the programming languages most commonly used to develop machine learning algorithms include Python, MATLAB, and C/C ++. However, none of these languages well balance both efficiency and simplicity. The Julia language is a fast, easy-to-use, and open-source programming language that was originally designed for high-performance computing, which can well balance the efficiency and simplicity. This paper summarizes the related research work and developments in the application of the Julia language in machine learning. It first surveys the popular machine learning algorithms that are developed in the Julia language. Then, it investigates applications of the machine learning algorithms implemented with the Julia language. Finally, it discusses the open issues and the potential future directions that arise in the use of the Julia language in machine learning.