Kernel Methods for the Approximation of the Eigenfunctions of the Koopman Operator

The Koopman operator provides a linear framework to study nonlinear dynamical systems. Its spectra offer valuable insights into system dynamics, but the operator can exhibit both discrete and continuous spectra, complicating direct computations. In this paper, we introduce a kernel-based method to construct the principal eigenfunctions of the Koopman operator without explicitly computing the operator itself. These principal eigenfunctions are associated with the equilibrium dynamics, and their eigenvalues match those of the linearization of the nonlinear system at the equilibrium point. We exploit the structure of the principal eigenfunctions by decomposing them into linear and nonlinear components. The linear part corresponds to the left eigenvector of the system's linearization at the equilibrium, while the nonlinear part is obtained by solving a partial differential equation (PDE) using kernel methods. Our approach avoids common issues such as spectral pollution and spurious eigenvalues, which can arise in previous methods. We demonstrate the effectiveness of our algorithm through numerical examples.

Separation Power of Equivariant Neural Networks

The separation power of a machine learning model refers to its capacity to distinguish distinct inputs, and it is often employed as a proxy for its expressivity. In this paper, we propose a theoretical framework to investigate the separation power of equivariant neural networks with point-wise activations. Using the proposed framework, we can derive an explicit description of inputs indistinguishable by a family of neural networks with given architecture, demonstrating that it remains unaffected by the choice of non-polynomial activation function employed. We are able to understand the role played by activation functions in separability. Indeed, we show that all non-polynomial activations, such as ReLU and sigmoid, are equivalent in terms of expressivity, and that they reach maximum discrimination capacity. We demonstrate how assessing the separation power of an equivariant neural network can be simplified to evaluating the separation power of minimal representations. We conclude by illustrating how these minimal components form a hierarchy in separation power.

A Characterization Theorem for Equivariant Networks with Point-wise Activations

Equivariant neural networks have shown improved performance, expressiveness and sample complexity on symmetrical domains. But for some specific symmetries, representations, and choice of coordinates, the most common point-wise activations, such as ReLU, are not equivariant, hence they cannot be employed in the design of equivariant neural networks. The theorem we present in this paper describes all possible combinations of finite-dimensional representations, choice of coordinates and point-wise activations to obtain an exactly equivariant layer, generalizing and strengthening existing characterizations. Notable cases of practical relevance are discussed as corollaries. Indeed, we prove that rotation-equivariant networks can only be invariant, as it happens for any network which is equivariant with respect to connected compact groups. Then, we discuss implications of our findings when applied to important instances of exactly equivariant networks. First, we completely characterize permutation equivariant networks such as Invariant Graph Networks with point-wise nonlinearities and their geometric counterparts, highlighting a plethora of models whose expressive power and performance are still unknown. Second, we show that feature spaces of disentangled steerable convolutional neural networks are trivial representations.

Quantitative and Qualitative Evaluation of Reinforcement Learning Policies for Autonomous Vehicles

Optimizing traffic dynamics in an evolving transportation landscape is crucial, particularly in scenarios where autonomous vehicles (AVs) with varying levels of autonomy coexist with human-driven cars. This paper presents a novel approach to optimizing choices of AVs using Proximal Policy Optimization (PPO), a reinforcement learning algorithm. We learned a policy to minimize traffic jams (i.e., minimize the time to cross the scenario) and to minimize pollution in a roundabout in Milan, Italy. Through empirical analysis, we demonstrate that our approach can reduce time and pollution levels. Furthermore, we qualitatively evaluate the learned policy using a cutting-edge cockpit to assess its performance in near-real-world conditions. To gauge the practicality and acceptability of the policy, we conducted evaluations with human participants using the simulator, focusing on a range of metrics like traffic smoothness and safety perception. In general, our findings show that human-driven vehicles benefit from optimizing AVs dynamics. Also, participants in the study highlighted that the scenario with 80\% AVs is perceived as safer than the scenario with 20\%. The same result is obtained for traffic smoothness perception.

Graph Neural Networks for temporal graphs: State of the art, open challenges, and opportunities

Graph Neural Networks (GNNs) have become the leading paradigm for learning on (static) graph-structured data. However, many real-world systems are dynamic in nature, since the graph and node/edge attributes change over time. In recent years, GNN-based models for temporal graphs have emerged as a promising area of research to extend the capabilities of GNNs. In this work, we provide the first comprehensive overview of the current state-of-the-art of temporal GNN, introducing a rigorous formalization of learning settings and tasks and a novel taxonomy categorizing existing approaches in terms of how the temporal aspect is represented and processed. We conclude the survey with a discussion of the most relevant open challenges for the field, from both research and application perspectives.

Interpolation with the polynomial kernels

The polynomial kernels are widely used in machine learning and they are one of the default choices to develop kernel-based classification and regression models. However, they are rarely used and considered in numerical analysis due to their lack of strict positive definiteness. In particular they do not enjoy the usual property of unisolvency for arbitrary point sets, which is one of the key properties used to build kernel-based interpolation methods. This paper is devoted to establish some initial results for the study of these kernels, and their related interpolation algorithms, in the context of approximation theory. We will first prove necessary and sufficient conditions on point sets which guarantee the existence and uniqueness of an interpolant. We will then study the Reproducing Kernel Hilbert Spaces (or native spaces) of these kernels and their norms, and provide inclusion relations between spaces corresponding to different kernel parameters. With these spaces at hand, it will be further possible to derive generic error estimates which apply to sufficiently smooth functions, thus escaping the native space. Finally, we will show how to employ an efficient stable algorithm to these kernels to obtain accurate interpolants, and we will test them in some numerical experiment. After this analysis several computational and theoretical aspects remain open, and we will outline possible further research directions in a concluding section. This work builds some bridges between kernel and polynomial interpolation, two topics to which the authors, to different extents, have been introduced under the supervision or through the work of Stefano De Marchi. For this reason, they wish to dedicate this work to him in the occasion of his 60th birthday.

Explaining the Explainers in Graph Neural Networks: a Comparative Study

Following a fast initial breakthrough in graph based learning, Graph Neural Networks (GNNs) have reached a widespread application in many science and engineering fields, prompting the need for methods to understand their decision process. GNN explainers have started to emerge in recent years, with a multitude of methods both novel or adapted from other domains. To sort out this plethora of alternative approaches, several studies have benchmarked the performance of different explainers in terms of various explainability metrics. However, these earlier works make no attempts at providing insights into why different GNN architectures are more or less explainable, or which explainer should be preferred in a given setting. In this survey, we fill these gaps by devising a systematic experimental study, which tests ten explainers on eight representative architectures trained on six carefully designed graph and node classification datasets. With our results we provide key insights on the choice and applicability of GNN explainers, we isolate key components that make them usable and successful and provide recommendations on how to avoid common interpretation pitfalls. We conclude by highlighting open questions and directions of possible future research.

A Framework for Verifiable and Auditable Federated Anomaly Detection

Federated Leaning is an emerging approach to manage cooperation between a group of agents for the solution of Machine Learning tasks, with the goal of improving each agent's performance without disclosing any data. In this paper we present a novel algorithmic architecture that tackle this problem in the particular case of Anomaly Detection (or classification or rare events), a setting where typical applications often comprise data with sensible information, but where the scarcity of anomalous examples encourages collaboration. We show how Random Forests can be used as a tool for the development of accurate classifiers with an effective insight-sharing mechanism that does not break the data integrity. Moreover, we explain how the new architecture can be readily integrated in a blockchain infrastructure to ensure the verifiable and auditable execution of the algorithm. Furthermore, we discuss how this work may set the basis for a more general approach for the design of federated ensemble-learning methods beyond the specific task and architecture discussed in this paper.

Reprogramming FairGANs with Variational Auto-Encoders: A New Transfer Learning Model

Fairness-aware GANs (FairGANs) exploit the mechanisms of Generative Adversarial Networks (GANs) to impose fairness on the generated data, freeing them from both disparate impact and disparate treatment. Given the model's advantages and performance, we introduce a novel learning framework to transfer a pre-trained FairGAN to other tasks. This reprogramming process has the goal of maintaining the FairGAN's main targets of data utility, classification utility, and data fairness, while widening its applicability and ease of use. In this paper we present the technical extensions required to adapt the original architecture to this new framework (and in particular the use of Variational Auto-Encoders), and discuss the benefits, trade-offs, and limitations of the new model.

Universality and Optimality of Structured Deep Kernel Networks

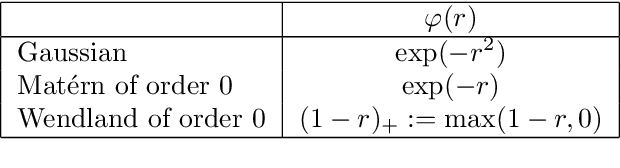
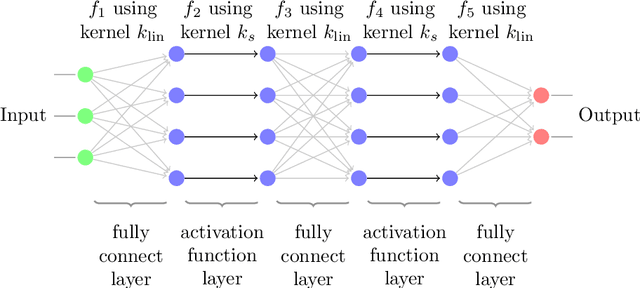
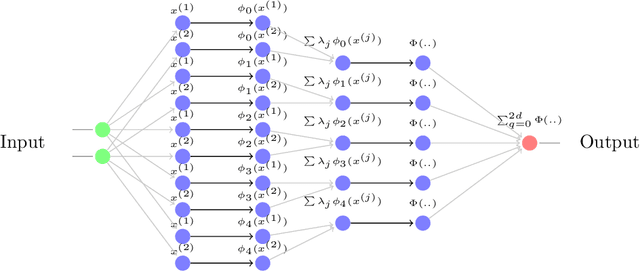
Kernel based methods yield approximation models that are flexible, efficient and powerful. In particular, they utilize fixed feature maps of the data, being often associated to strong analytical results that prove their accuracy. On the other hand, the recent success of machine learning methods has been driven by deep neural networks (NNs). They achieve a significant accuracy on very high-dimensional data, in that they are able to learn also efficient data representations or data-based feature maps. In this paper, we leverage a recent deep kernel representer theorem to connect the two approaches and understand their interplay. In particular, we show that the use of special types of kernels yield models reminiscent of neural networks that are founded in the same theoretical framework of classical kernel methods, while enjoying many computational properties of deep neural networks. Especially the introduced Structured Deep Kernel Networks (SDKNs) can be viewed as neural networks with optimizable activation functions obeying a representer theorem. Analytic properties show their universal approximation properties in different asymptotic regimes of unbounded number of centers, width and depth. Especially in the case of unbounded depth, the constructions is asymptotically better than corresponding constructions for ReLU neural networks, which is made possible by the flexibility of kernel approximation