Finetuning greedy kernel models by exchange algorithms

Kernel based approximation offers versatile tools for high-dimensional approximation, which can especially be leveraged for surrogate modeling. For this purpose, both "knot insertion" and "knot removal" approaches aim at choosing a suitable subset of the data, in order to obtain a sparse but nevertheless accurate kernel model. In the present work, focussing on kernel based interpolation, we aim at combining these two approaches to further improve the accuracy of kernel models, without increasing the computational complexity of the final kernel model. For this, we introduce a class of kernel exchange algorithms (KEA). The resulting KEA algorithm can be used for finetuning greedy kernel surrogate models, allowing for an reduction of the error up to 86.4% (17.2% on average) in our experiments.

Universality and Optimality of Structured Deep Kernel Networks

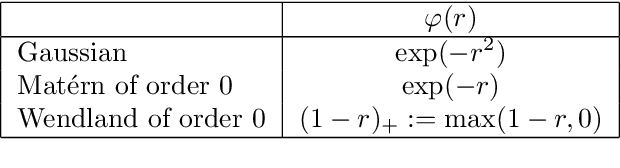
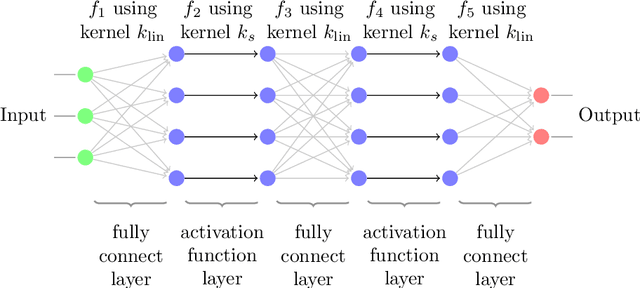
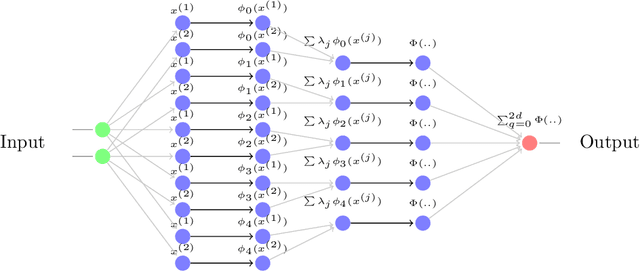
Kernel based methods yield approximation models that are flexible, efficient and powerful. In particular, they utilize fixed feature maps of the data, being often associated to strong analytical results that prove their accuracy. On the other hand, the recent success of machine learning methods has been driven by deep neural networks (NNs). They achieve a significant accuracy on very high-dimensional data, in that they are able to learn also efficient data representations or data-based feature maps. In this paper, we leverage a recent deep kernel representer theorem to connect the two approaches and understand their interplay. In particular, we show that the use of special types of kernels yield models reminiscent of neural networks that are founded in the same theoretical framework of classical kernel methods, while enjoying many computational properties of deep neural networks. Especially the introduced Structured Deep Kernel Networks (SDKNs) can be viewed as neural networks with optimizable activation functions obeying a representer theorem. Analytic properties show their universal approximation properties in different asymptotic regimes of unbounded number of centers, width and depth. Especially in the case of unbounded depth, the constructions is asymptotically better than corresponding constructions for ReLU neural networks, which is made possible by the flexibility of kernel approximation

Structured Deep Kernel Networks for Data-Driven Closure Terms of Turbulent Flows

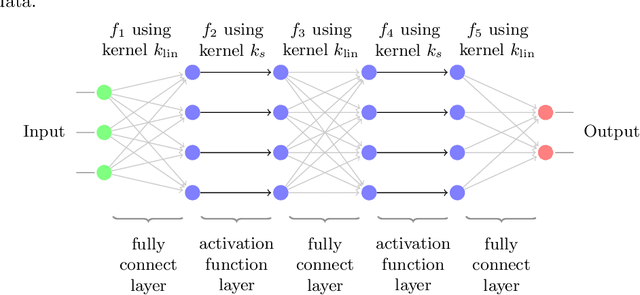
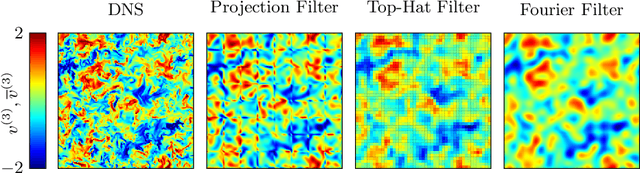
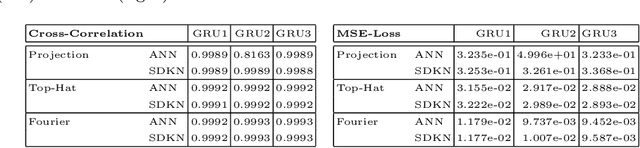
Standard kernel methods for machine learning usually struggle when dealing with large datasets. We review a recently introduced Structured Deep Kernel Network (SDKN) approach that is capable of dealing with high-dimensional and huge datasets - and enjoys typical standard machine learning approximation properties. We extend the SDKN to combine it with standard machine learning modules and compare it with Neural Networks on the scientific challenge of data-driven prediction of closure terms of turbulent flows. We show experimentally that the SDKNs are capable of dealing with large datasets and achieve near-perfect accuracy on the given application.

Biomechanical surrogate modelling using stabilized vectorial greedy kernel methods

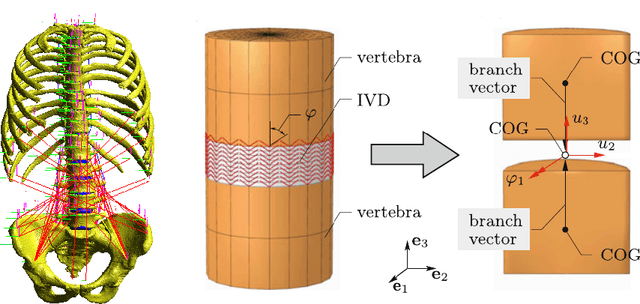
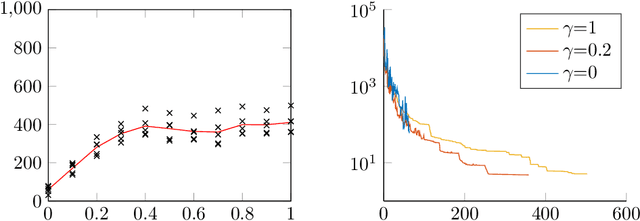
Greedy kernel approximation algorithms are successful techniques for sparse and accurate data-based modelling and function approximation. Based on a recent idea of stabilization of such algorithms in the scalar output case, we here consider the vectorial extension built on VKOGA. We introduce the so called $\gamma$-restricted VKOGA, comment on analytical properties and present numerical evaluation on data from a clinically relevant application, the modelling of the human spine. The experiments show that the new stabilized algorithms result in improved accuracy and stability over the non-stabilized algorithms.