Universality and Optimality of Structured Deep Kernel Networks
Paper and Code
May 15, 2021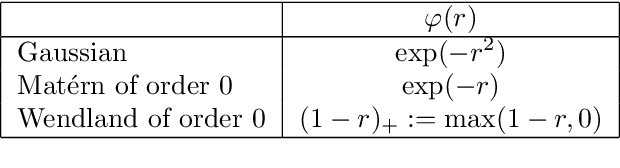
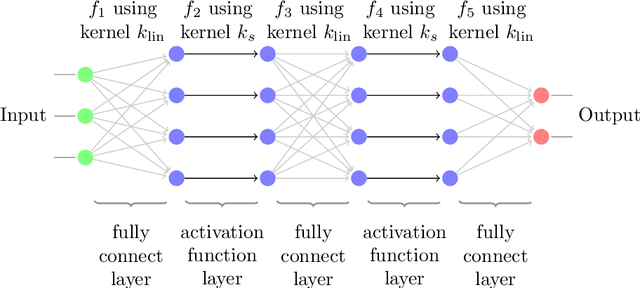

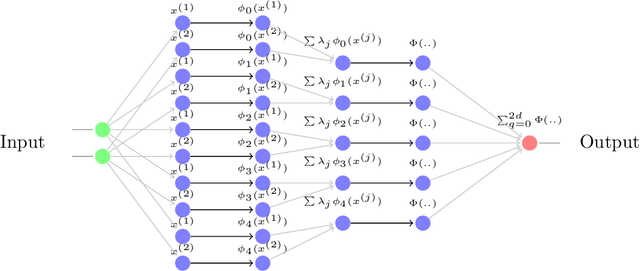
Kernel based methods yield approximation models that are flexible, efficient and powerful. In particular, they utilize fixed feature maps of the data, being often associated to strong analytical results that prove their accuracy. On the other hand, the recent success of machine learning methods has been driven by deep neural networks (NNs). They achieve a significant accuracy on very high-dimensional data, in that they are able to learn also efficient data representations or data-based feature maps. In this paper, we leverage a recent deep kernel representer theorem to connect the two approaches and understand their interplay. In particular, we show that the use of special types of kernels yield models reminiscent of neural networks that are founded in the same theoretical framework of classical kernel methods, while enjoying many computational properties of deep neural networks. Especially the introduced Structured Deep Kernel Networks (SDKNs) can be viewed as neural networks with optimizable activation functions obeying a representer theorem. Analytic properties show their universal approximation properties in different asymptotic regimes of unbounded number of centers, width and depth. Especially in the case of unbounded depth, the constructions is asymptotically better than corresponding constructions for ReLU neural networks, which is made possible by the flexibility of kernel approximation
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge