Marius Kurz
Harnessing Equivariance: Modeling Turbulence with Graph Neural Networks
Apr 10, 2025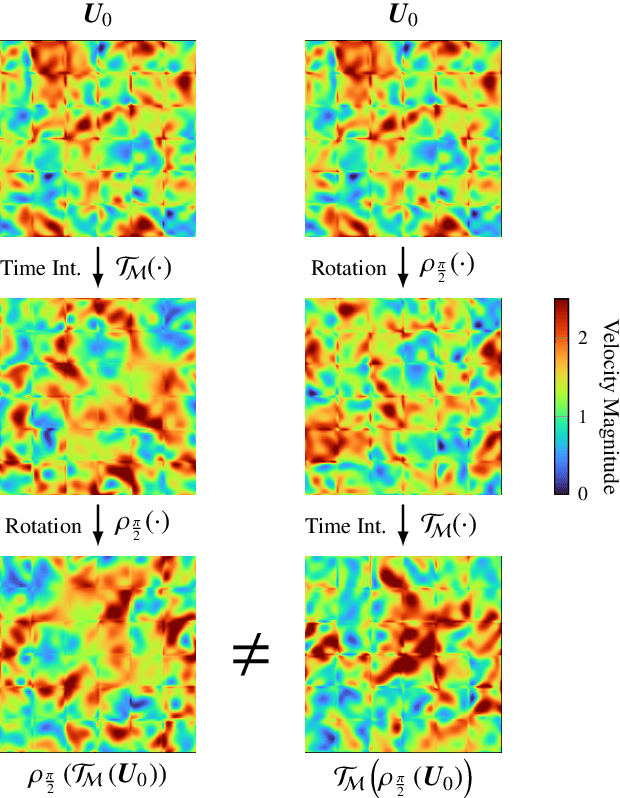
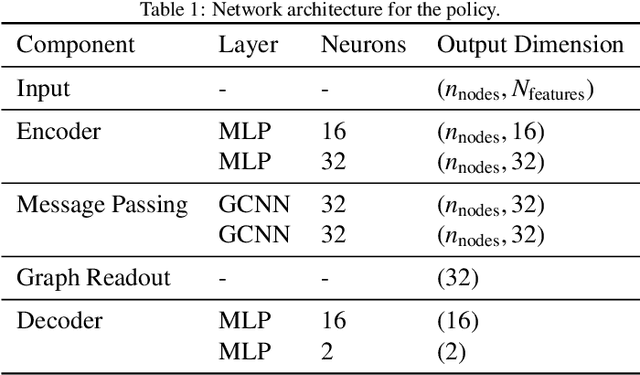
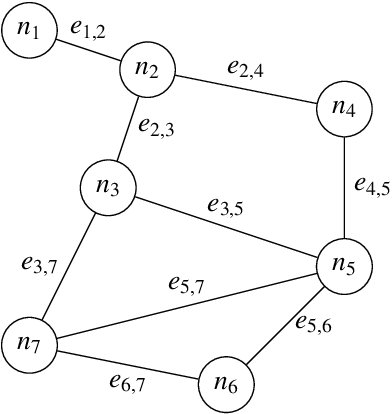

Abstract:This work proposes a novel methodology for turbulence modeling in Large Eddy Simulation (LES) based on Graph Neural Networks (GNNs), which embeds the discrete rotational, reflectional and translational symmetries of the Navier-Stokes equations into the model architecture. In addition, suitable invariant input and output spaces are derived that allow the GNN models to be embedded seamlessly into the LES framework to obtain a symmetry-preserving simulation setup. The suitability of the proposed approach is investigated for two canonical test cases: Homogeneous Isotropic Turbulence (HIT) and turbulent channel flow. For both cases, GNN models are trained successfully in actual simulations using Reinforcement Learning (RL) to ensure that the models are consistent with the underlying LES formulation and discretization. It is demonstrated for the HIT case that the resulting GNN-based LES scheme recovers rotational and reflectional equivariance up to machine precision in actual simulations. At the same time, the stability and accuracy remain on par with non-symmetry-preserving machine learning models that fail to obey these properties. The same modeling strategy translates well to turbulent channel flow, where the GNN model successfully learns the more complex flow physics and is able to recover the turbulent statistics and Reynolds stresses. It is shown that the GNN model learns a zonal modeling strategy with distinct behaviors in the near-wall and outer regions. The proposed approach thus demonstrates the potential of GNNs for turbulence modeling, especially in the context of LES and RL.
Invariant Control Strategies for Active Flow Control using Graph Neural Networks
Mar 28, 2025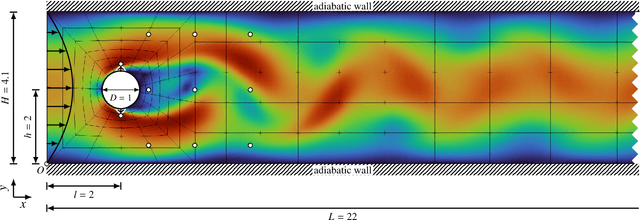
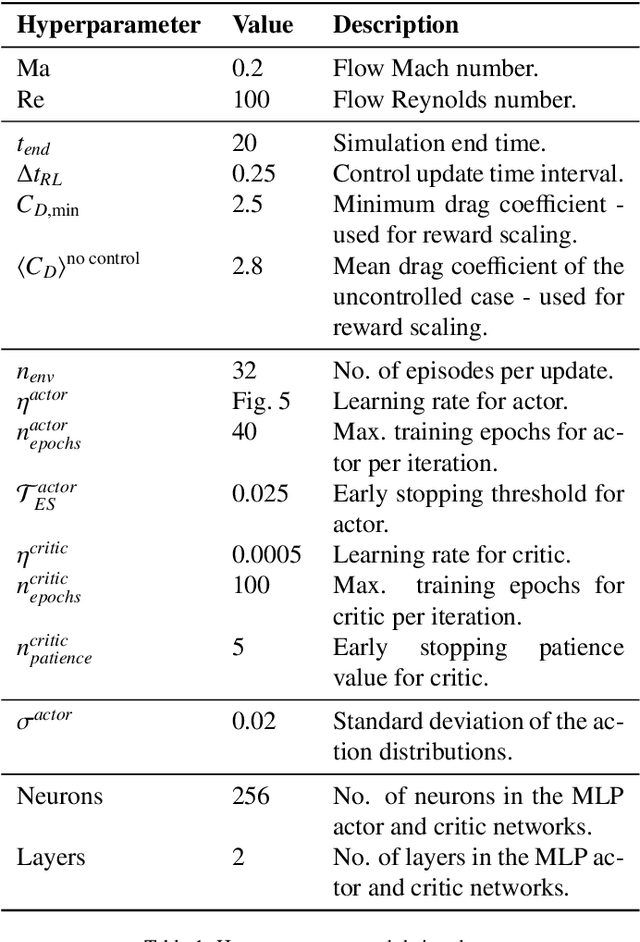
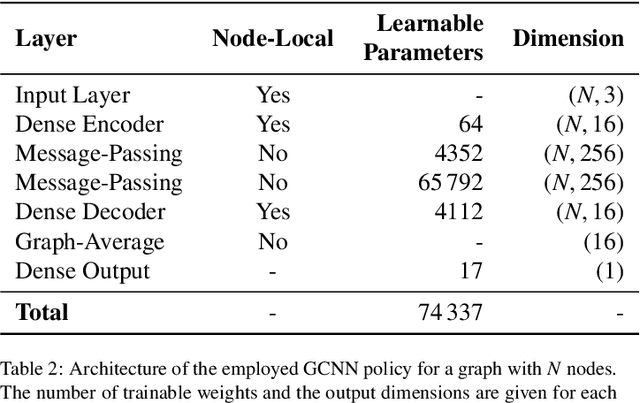
Abstract:Reinforcement learning has gained traction for active flow control tasks, with initial applications exploring drag mitigation via flow field augmentation around a two-dimensional cylinder. RL has since been extended to more complex turbulent flows and has shown significant potential in learning complex control strategies. However, such applications remain computationally challenging due to its sample inefficiency and associated simulation costs. This fact is worsened by the lack of generalization capabilities of these trained policy networks, often being implicitly tied to the input configurations of their training conditions. In this work, we propose the use of graph neural networks to address this particular limitation, effectively increasing the range of applicability and getting more value out of the upfront RL training cost. GNNs can naturally process unstructured, threedimensional flow data, preserving spatial relationships without the constraints of a Cartesian grid. Additionally, they incorporate rotational, reflectional, and permutation invariance into the learned control policies, thus improving generalization and thereby removing the shortcomings of commonly used CNN or MLP architectures. To demonstrate the effectiveness of this approach, we revisit the well-established two-dimensional cylinder benchmark problem for active flow control. The RL training is implemented using Relexi, a high-performance RL framework, with flow simulations conducted in parallel using the high-order discontinuous Galerkin framework FLEXI. Our results show that GNN-based control policies achieve comparable performance to existing methods while benefiting from improved generalization properties. This work establishes GNNs as a promising architecture for RL-based flow control and highlights the capabilities of Relexi and FLEXI for large-scale RL applications in fluid dynamics.
Toward Discretization-Consistent Closure Schemes for Large Eddy Simulation Using Reinforcement Learning
Sep 12, 2023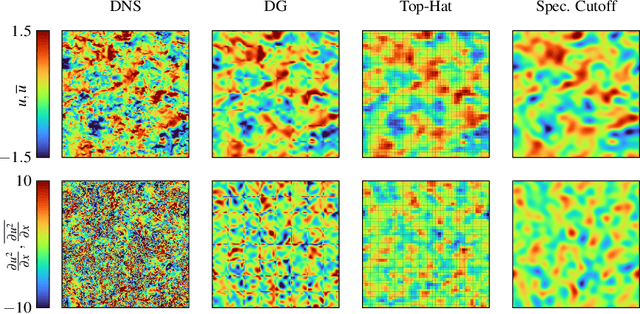
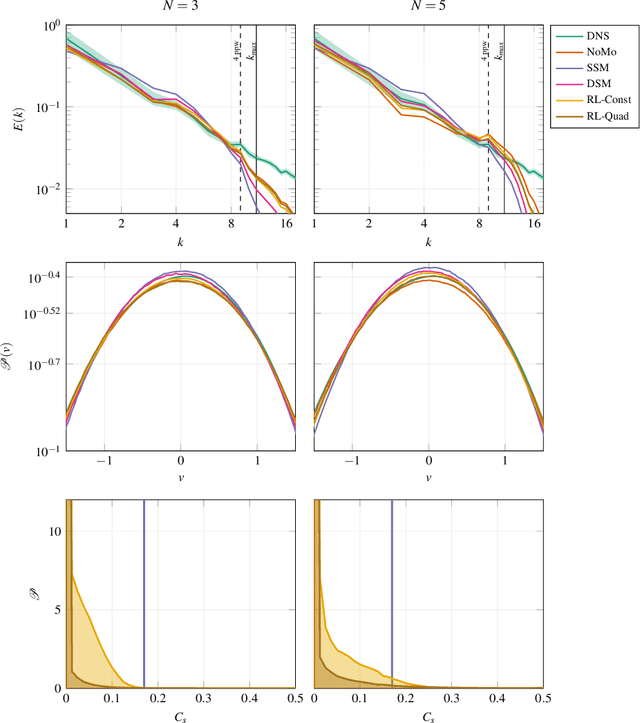
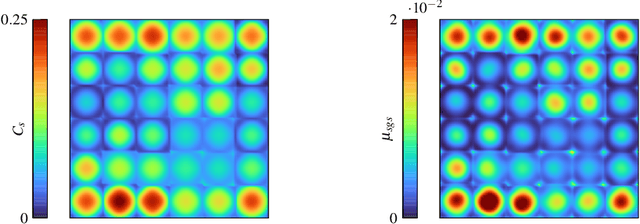
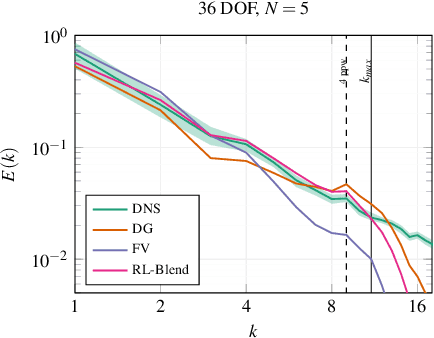
Abstract:We propose a novel method for developing discretization-consistent closure schemes for implicitly filtered Large Eddy Simulation (LES). In implicitly filtered LES, the induced filter kernel, and thus the closure terms, are determined by the properties of the grid and the discretization operator, leading to additional computational subgrid terms that are generally unknown in a priori analysis. Therefore, the task of adapting the coefficients of LES closure models is formulated as a Markov decision process and solved in an a posteriori manner with Reinforcement Learning (RL). This allows to adjust the model to the actual discretization as it also incorporates the interaction between the discretization and the model itself. This optimization framework is applied to both explicit and implicit closure models. An element-local eddy viscosity model is optimized as the explicit model. For the implicit modeling, RL is applied to identify an optimal blending strategy for a hybrid discontinuous Galerkin (DG) and finite volume scheme. All newly derived models achieve accurate and consistent results, either matching or outperforming classical state-of-the-art models for different discretizations and resolutions. Moreover, the explicit model is demonstrated to adapt its distribution of viscosity within the DG elements to the inhomogeneous discretization properties of the operator. In the implicit case, the optimized hybrid scheme renders itself as a viable modeling ansatz that could initiate a new class of high order schemes for compressible turbulence. Overall, the results demonstrate that the proposed RL optimization can provide discretization-consistent closures that could reduce the uncertainty in implicitly filtered LES.
Deep Reinforcement Learning for Turbulence Modeling in Large Eddy Simulations
Jun 21, 2022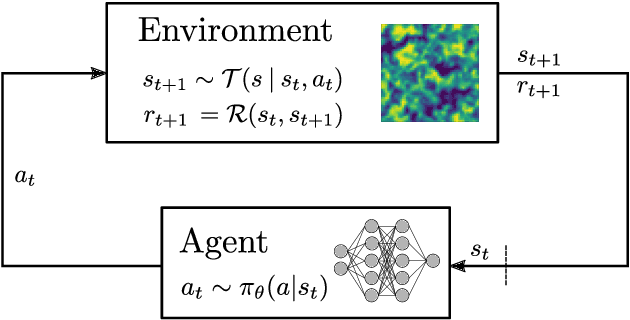

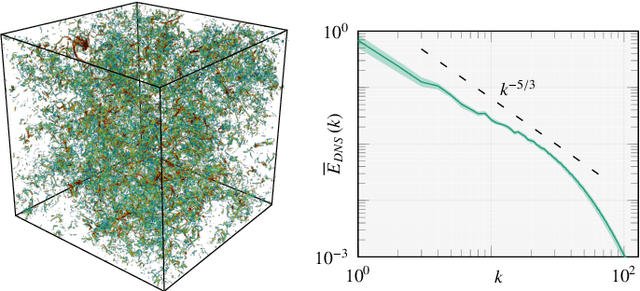
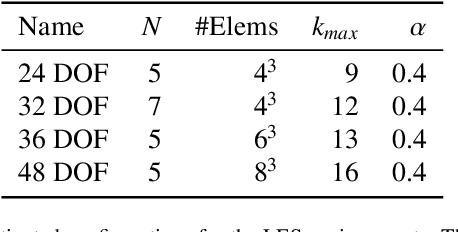
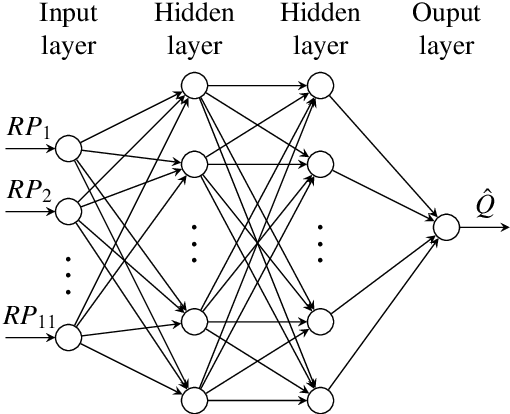
Abstract:Over the last years, supervised learning (SL) has established itself as the state-of-the-art for data-driven turbulence modeling. In the SL paradigm, models are trained based on a dataset, which is typically computed a priori from a high-fidelity solution by applying the respective filter function, which separates the resolved and the unresolved flow scales. For implicitly filtered large eddy simulation (LES), this approach is infeasible, since here, the employed discretization itself acts as an implicit filter function. As a consequence, the exact filter form is generally not known and thus, the corresponding closure terms cannot be computed even if the full solution is available. The reinforcement learning (RL) paradigm can be used to avoid this inconsistency by training not on a previously obtained training dataset, but instead by interacting directly with the dynamical LES environment itself. This allows to incorporate the potentially complex implicit LES filter into the training process by design. In this work, we apply a reinforcement learning framework to find an optimal eddy-viscosity for implicitly filtered large eddy simulations of forced homogeneous isotropic turbulence. For this, we formulate the task of turbulence modeling as an RL task with a policy network based on convolutional neural networks that adapts the eddy-viscosity in LES dynamically in space and time based on the local flow state only. We demonstrate that the trained models can provide long-term stable simulations and that they outperform established analytical models in terms of accuracy. In addition, the models generalize well to other resolutions and discretizations. We thus demonstrate that RL can provide a framework for consistent, accurate and stable turbulence modeling especially for implicitly filtered LES.
Deep Reinforcement Learning for Computational Fluid Dynamics on HPC Systems
May 13, 2022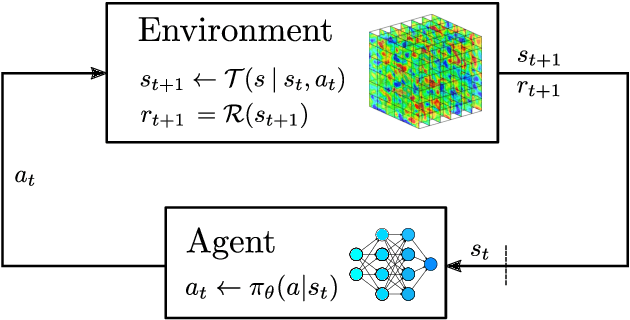

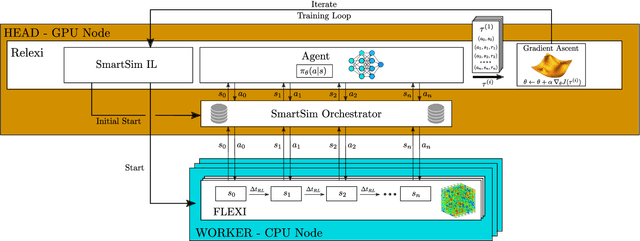
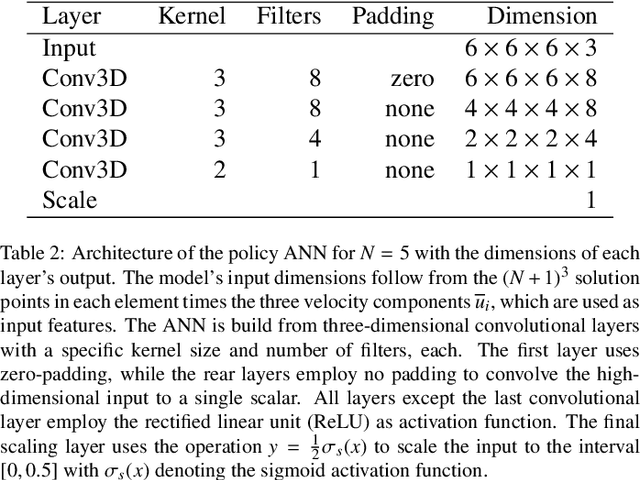
Abstract:Reinforcement learning (RL) is highly suitable for devising control strategies in the context of dynamical systems. A prominent instance of such a dynamical system is the system of equations governing fluid dynamics. Recent research results indicate that RL-augmented computational fluid dynamics (CFD) solvers can exceed the current state of the art, for example in the field of turbulence modeling. However, while in supervised learning, the training data can be generated a priori in an offline manner, RL requires constant run-time interaction and data exchange with the CFD solver during training. In order to leverage the potential of RL-enhanced CFD, the interaction between the CFD solver and the RL algorithm thus have to be implemented efficiently on high-performance computing (HPC) hardware. To this end, we present Relexi as a scalable RL framework that bridges the gap between machine learning workflows and modern CFD solvers on HPC systems providing both components with its specialized hardware. Relexi is built with modularity in mind and allows easy integration of various HPC solvers by means of the in-memory data transfer provided by the SmartSim library. Here, we demonstrate that the Relexi framework can scale up to hundreds of parallel environment on thousands of cores. This allows to leverage modern HPC resources to either enable larger problems or faster turnaround times. Finally, we demonstrate the potential of an RL-augmented CFD solver by finding a control strategy for optimal eddy viscosity selection in large eddy simulations.
Structured Deep Kernel Networks for Data-Driven Closure Terms of Turbulent Flows
Mar 25, 2021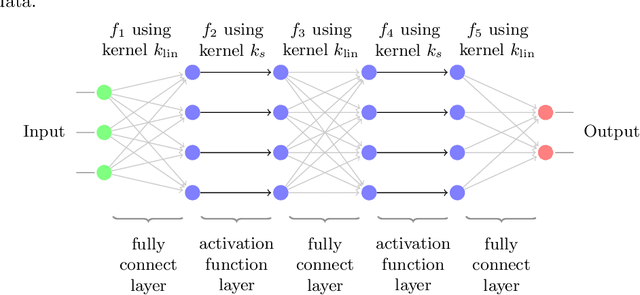
Abstract:Standard kernel methods for machine learning usually struggle when dealing with large datasets. We review a recently introduced Structured Deep Kernel Network (SDKN) approach that is capable of dealing with high-dimensional and huge datasets - and enjoys typical standard machine learning approximation properties. We extend the SDKN to combine it with standard machine learning modules and compare it with Neural Networks on the scientific challenge of data-driven prediction of closure terms of turbulent flows. We show experimentally that the SDKNs are capable of dealing with large datasets and achieve near-perfect accuracy on the given application.
A Perspective on Machine Learning Methods in Turbulence Modelling
Oct 23, 2020
Abstract:This work presents a review of the current state of research in data-driven turbulence closure modeling. It offers a perspective on the challenges and open issues, but also on the advantages and promises of machine learning methods applied to parameter estimation, model identification, closure term reconstruction and beyond, mostly from the perspective of Large Eddy Simulation and related techniques. We stress that consistency of the training data, the model, the underlying physics and the discretization is a key issue that needs to be considered for a successful ML-augmented modeling strategy. In order to make the discussion useful for non-experts in either field, we introduce both the modeling problem in turbulence as well as the prominent ML paradigms and methods in a concise and self-consistent manner. Following, we present a survey of the current data-driven model concepts and methods, highlight important developments and put them into the context of the discussed challenges.
A machine learning framework for LES closure terms
Oct 01, 2020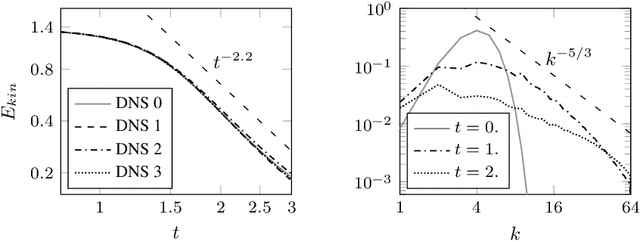
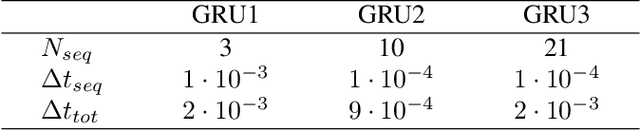
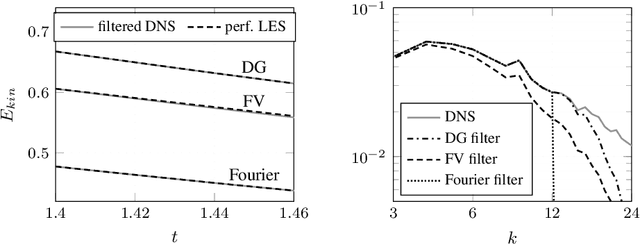
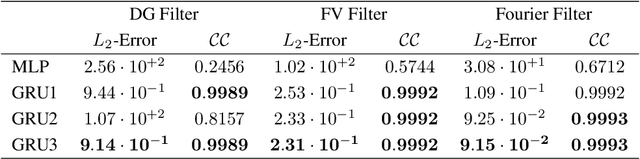
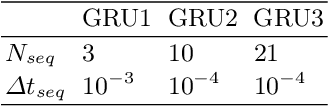
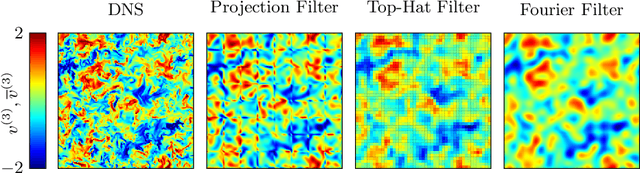
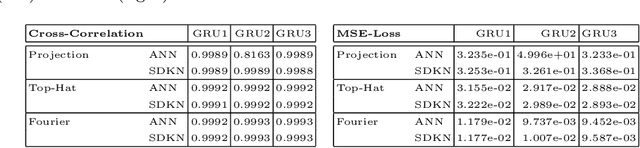
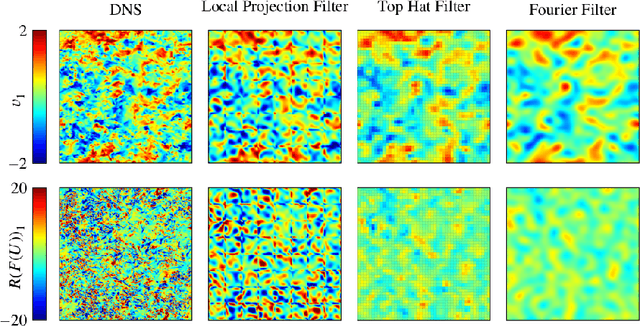
Abstract:In the present work, we explore the capability of artificial neural networks (ANN) to predict the closure terms for large eddy simulations (LES) solely from coarse-scale data. To this end, we derive a consistent framework for LES closure models, with special emphasis laid upon the incorporation of implicit discretization-based filters and numerical approximation errors. We investigate implicit filter types, which are inspired by the solution representation of discontinuous Galerkin and finite volume schemes and mimic the behaviour of the discretization operator, and a global Fourier cutoff filter as a representative of a typical explicit LES filter. Within the perfect LES framework, we compute the exact closure terms for the different LES filter functions from direct numerical simulation results of decaying homogeneous isotropic turbulence. Multiple ANN with a multilayer perceptron (MLP) or a gated recurrent unit (GRU) architecture are trained to predict the computed closure terms solely from coarse-scale input data. For the given application, the GRU architecture clearly outperforms the MLP networks in terms of accuracy, whilst reaching up to 99.9% cross-correlation between the networks' predictions and the exact closure terms for all considered filter functions. The GRU networks are also shown to generalize well across different LES filters and resolutions. The present study can thus be seen as a starting point for the investigation of data-based modeling approaches for LES, which not only include the physical closure terms, but account for the discretization effects in implicitly filtered LES as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge