Toward Discretization-Consistent Closure Schemes for Large Eddy Simulation Using Reinforcement Learning

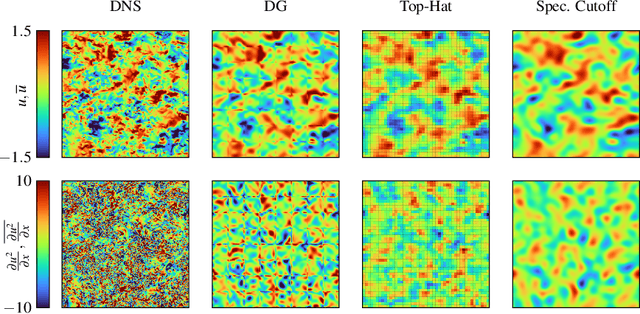
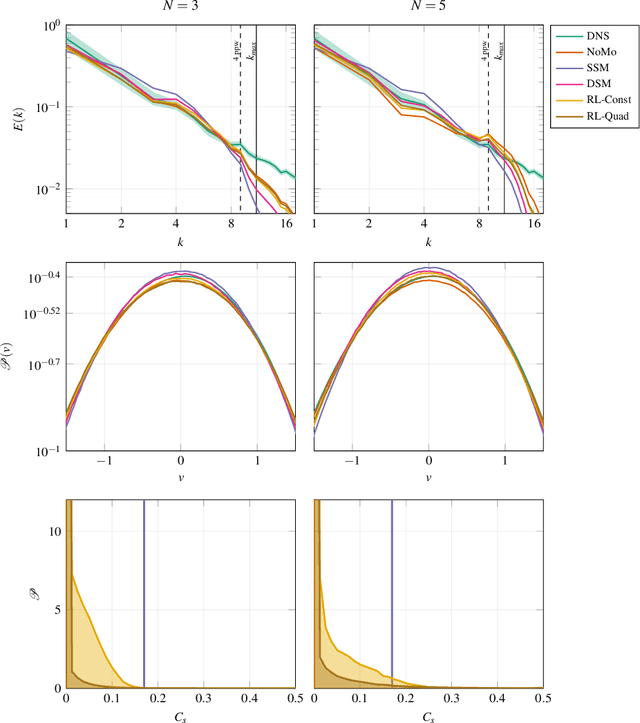
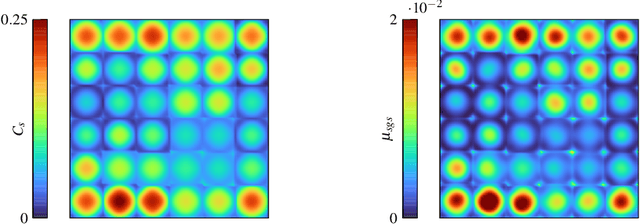
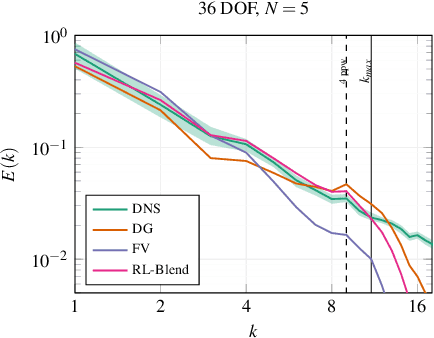
We propose a novel method for developing discretization-consistent closure schemes for implicitly filtered Large Eddy Simulation (LES). In implicitly filtered LES, the induced filter kernel, and thus the closure terms, are determined by the properties of the grid and the discretization operator, leading to additional computational subgrid terms that are generally unknown in a priori analysis. Therefore, the task of adapting the coefficients of LES closure models is formulated as a Markov decision process and solved in an a posteriori manner with Reinforcement Learning (RL). This allows to adjust the model to the actual discretization as it also incorporates the interaction between the discretization and the model itself. This optimization framework is applied to both explicit and implicit closure models. An element-local eddy viscosity model is optimized as the explicit model. For the implicit modeling, RL is applied to identify an optimal blending strategy for a hybrid discontinuous Galerkin (DG) and finite volume scheme. All newly derived models achieve accurate and consistent results, either matching or outperforming classical state-of-the-art models for different discretizations and resolutions. Moreover, the explicit model is demonstrated to adapt its distribution of viscosity within the DG elements to the inhomogeneous discretization properties of the operator. In the implicit case, the optimized hybrid scheme renders itself as a viable modeling ansatz that could initiate a new class of high order schemes for compressible turbulence. Overall, the results demonstrate that the proposed RL optimization can provide discretization-consistent closures that could reduce the uncertainty in implicitly filtered LES.