Deep Reinforcement Learning for Turbulence Modeling in Large Eddy Simulations
Paper and Code
Jun 21, 2022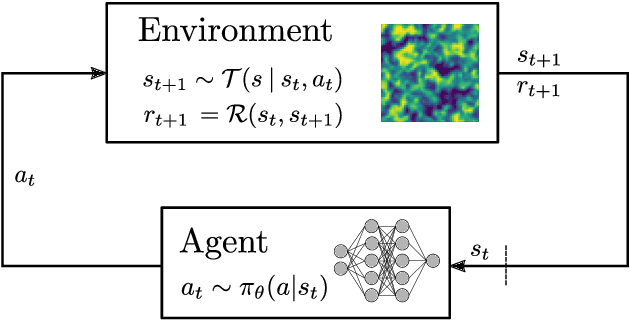

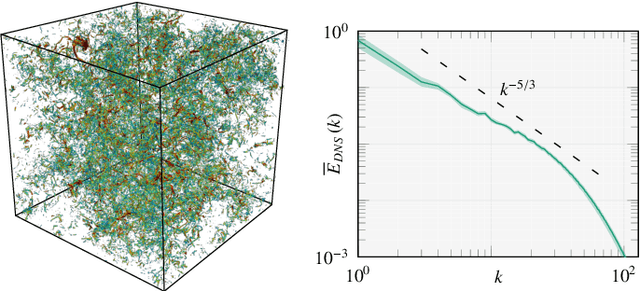
Over the last years, supervised learning (SL) has established itself as the state-of-the-art for data-driven turbulence modeling. In the SL paradigm, models are trained based on a dataset, which is typically computed a priori from a high-fidelity solution by applying the respective filter function, which separates the resolved and the unresolved flow scales. For implicitly filtered large eddy simulation (LES), this approach is infeasible, since here, the employed discretization itself acts as an implicit filter function. As a consequence, the exact filter form is generally not known and thus, the corresponding closure terms cannot be computed even if the full solution is available. The reinforcement learning (RL) paradigm can be used to avoid this inconsistency by training not on a previously obtained training dataset, but instead by interacting directly with the dynamical LES environment itself. This allows to incorporate the potentially complex implicit LES filter into the training process by design. In this work, we apply a reinforcement learning framework to find an optimal eddy-viscosity for implicitly filtered large eddy simulations of forced homogeneous isotropic turbulence. For this, we formulate the task of turbulence modeling as an RL task with a policy network based on convolutional neural networks that adapts the eddy-viscosity in LES dynamically in space and time based on the local flow state only. We demonstrate that the trained models can provide long-term stable simulations and that they outperform established analytical models in terms of accuracy. In addition, the models generalize well to other resolutions and discretizations. We thus demonstrate that RL can provide a framework for consistent, accurate and stable turbulence modeling especially for implicitly filtered LES.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge