Biomechanical surrogate modelling using stabilized vectorial greedy kernel methods
Paper and Code
Apr 28, 2020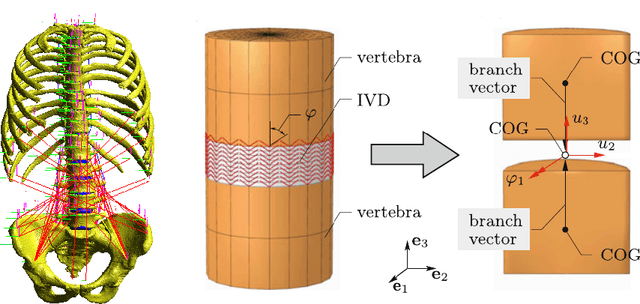


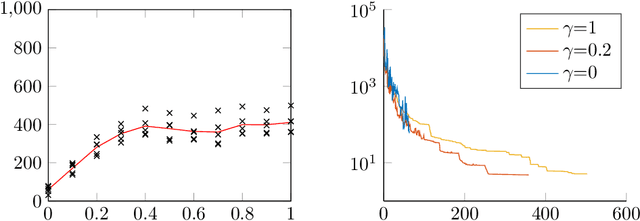
Greedy kernel approximation algorithms are successful techniques for sparse and accurate data-based modelling and function approximation. Based on a recent idea of stabilization of such algorithms in the scalar output case, we here consider the vectorial extension built on VKOGA. We introduce the so called $\gamma$-restricted VKOGA, comment on analytical properties and present numerical evaluation on data from a clinically relevant application, the modelling of the human spine. The experiments show that the new stabilized algorithms result in improved accuracy and stability over the non-stabilized algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge