Learning phase-space flows using time-discrete implicit Runge-Kutta PINNs

We present a computational framework for obtaining multidimensional phase-space solutions of systems of non-linear coupled differential equations, using high-order implicit Runge-Kutta Physics- Informed Neural Networks (IRK-PINNs) schemes. Building upon foundational work originally solving differential equations for fields depending on coordinates [J. Comput. Phys. 378, 686 (2019)], we adapt the scheme to a context where the coordinates are treated as functions. This modification enables us to efficiently solve equations of motion for a particle in an external field. Our scheme is particularly useful for explicitly time-independent and periodic fields. We apply this approach to successfully solve the equations of motion for a mass particle placed in a central force field and a charged particle in a periodic electric field.

Inducing Riesz and orthonormal bases in $L^2$ via composition operators

We investigate perturbations of orthonormal bases of $L^2$ via a composition operator $C_h$ induced by a mapping $h$. We provide a comprehensive characterization of the mapping $h$ required for the perturbed sequence to form an orthonormal or Riesz basis. Restricting our analysis to differentiable mappings, we reveal that all Riesz bases of the given form are induced by bi-Lipschitz mappings. In addition, we discuss implications of these results for approximation theory, highlighting the potential of using bijective neural networks to construct complete sequences with favorable approximation properties.

Finetuning greedy kernel models by exchange algorithms

Kernel based approximation offers versatile tools for high-dimensional approximation, which can especially be leveraged for surrogate modeling. For this purpose, both "knot insertion" and "knot removal" approaches aim at choosing a suitable subset of the data, in order to obtain a sparse but nevertheless accurate kernel model. In the present work, focussing on kernel based interpolation, we aim at combining these two approaches to further improve the accuracy of kernel models, without increasing the computational complexity of the final kernel model. For this, we introduce a class of kernel exchange algorithms (KEA). The resulting KEA algorithm can be used for finetuning greedy kernel surrogate models, allowing for an reduction of the error up to 86.4% (17.2% on average) in our experiments.

Computing excited states of molecules using normalizing flows

We present a new nonlinear variational framework for simultaneously computing ground and excited states of quantum systems. Our approach is based on approximating wavefunctions in the linear span of basis functions that are augmented and optimized \emph{via} composition with normalizing flows. The accuracy and efficiency of our approach are demonstrated in the calculations of a large number of vibrational states of the triatomic H$_2$S molecule as well as ground and several excited electronic states of prototypical one-electron systems including the hydrogen atom, the molecular hydrogen ion, and a carbon atom in a single-active-electron approximation. The results demonstrate significant improvements in the accuracy of energy predictions and accelerated basis-set convergence even when using normalizing flows with a small number of parameters. The present approach can be also seen as the optimization of a set of intrinsic coordinates that best capture the underlying physics within the given basis set.

Dimensionality Reduction and Wasserstein Stability for Kernel Regression

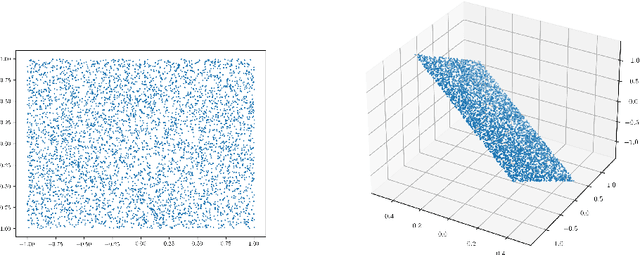
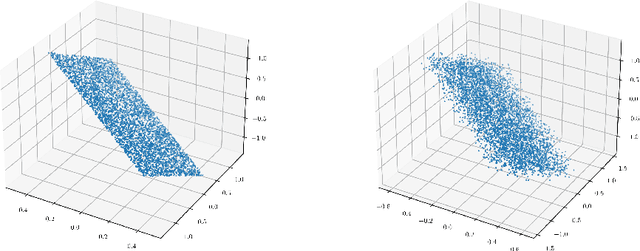
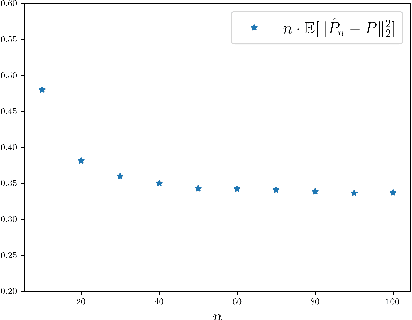
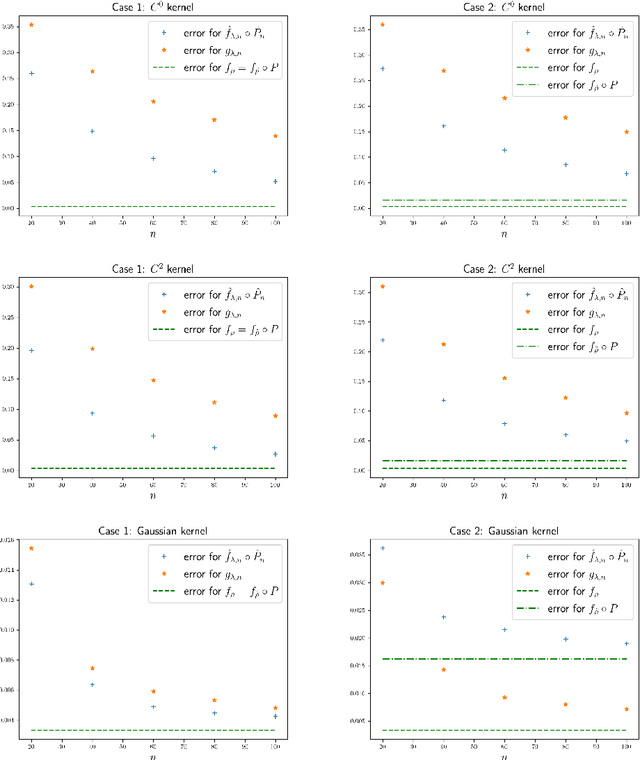
In a high-dimensional regression framework, we study consequences of the naive two-step procedure where first the dimension of the input variables is reduced and second, the reduced input variables are used to predict the output variable. More specifically we combine principal component analysis (PCA) with kernel regression. In order to analyze the resulting regression errors, a novel stability result of kernel regression with respect to the Wasserstein distance is derived. This allows us to bound errors that occur when perturbed input data is used to fit a kernel function. We combine the stability result with known estimates from the literature on both principal component analysis and kernel regression to obtain convergence rates for the two-step procedure.