Learning phase-space flows using time-discrete implicit Runge-Kutta PINNs

We present a computational framework for obtaining multidimensional phase-space solutions of systems of non-linear coupled differential equations, using high-order implicit Runge-Kutta Physics- Informed Neural Networks (IRK-PINNs) schemes. Building upon foundational work originally solving differential equations for fields depending on coordinates [J. Comput. Phys. 378, 686 (2019)], we adapt the scheme to a context where the coordinates are treated as functions. This modification enables us to efficiently solve equations of motion for a particle in an external field. Our scheme is particularly useful for explicitly time-independent and periodic fields. We apply this approach to successfully solve the equations of motion for a mass particle placed in a central force field and a charged particle in a periodic electric field.

Observation of Aerosolization-induced Morphological Changes in Viral Capsids

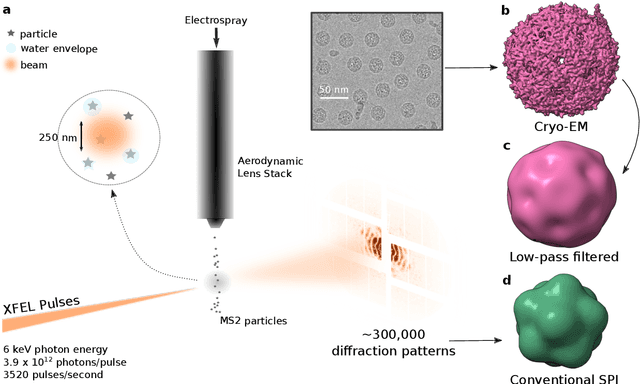
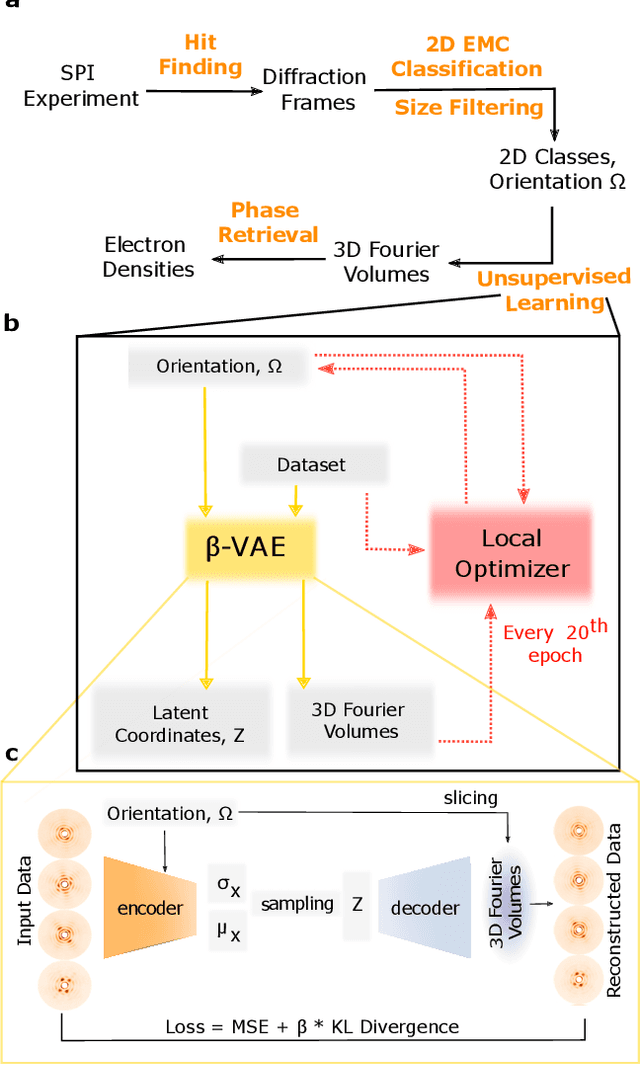
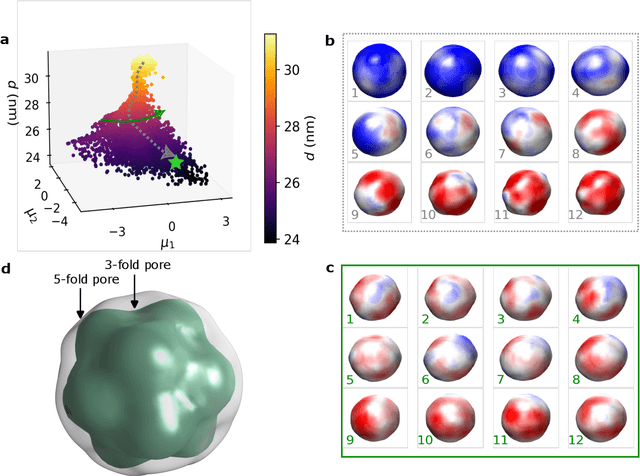
Single-stranded RNA viruses co-assemble their capsid with the genome and variations in capsid structures can have significant functional relevance. In particular, viruses need to respond to a dehydrating environment to prevent genomic degradation and remain active upon rehydration. Theoretical work has predicted low-energy buckling transitions in icosahedral capsids which could protect the virus from further dehydration. However, there has been no direct experimental evidence, nor molecular mechanism, for such behaviour. Here we observe this transition using X-ray single particle imaging of MS2 bacteriophages after aerosolization. Using a combination of machine learning tools, we classify hundreds of thousands of single particle diffraction patterns to learn the structural landscape of the capsid morphology as a function of time spent in the aerosol phase. We found a previously unreported compact conformation as well as intermediate structures which suggest an incoherent buckling transition which does not preserve icosahedral symmetry. Finally, we propose a mechanism of this buckling, where a single 19-residue loop is destabilised, leading to the large observed morphology change. Our results provide experimental evidence for a mechanism by which viral capsids protect themselves from dehydration. In the process, these findings also demonstrate the power of single particle X-ray imaging and machine learning methods in studying biomolecular structural dynamics.

Computing excited states of molecules using normalizing flows

We present a new nonlinear variational framework for simultaneously computing ground and excited states of quantum systems. Our approach is based on approximating wavefunctions in the linear span of basis functions that are augmented and optimized \emph{via} composition with normalizing flows. The accuracy and efficiency of our approach are demonstrated in the calculations of a large number of vibrational states of the triatomic H$_2$S molecule as well as ground and several excited electronic states of prototypical one-electron systems including the hydrogen atom, the molecular hydrogen ion, and a carbon atom in a single-active-electron approximation. The results demonstrate significant improvements in the accuracy of energy predictions and accelerated basis-set convergence even when using normalizing flows with a small number of parameters. The present approach can be also seen as the optimization of a set of intrinsic coordinates that best capture the underlying physics within the given basis set.

Unsupervised learning approaches to characterize heterogeneous samples using X-ray single particle imaging

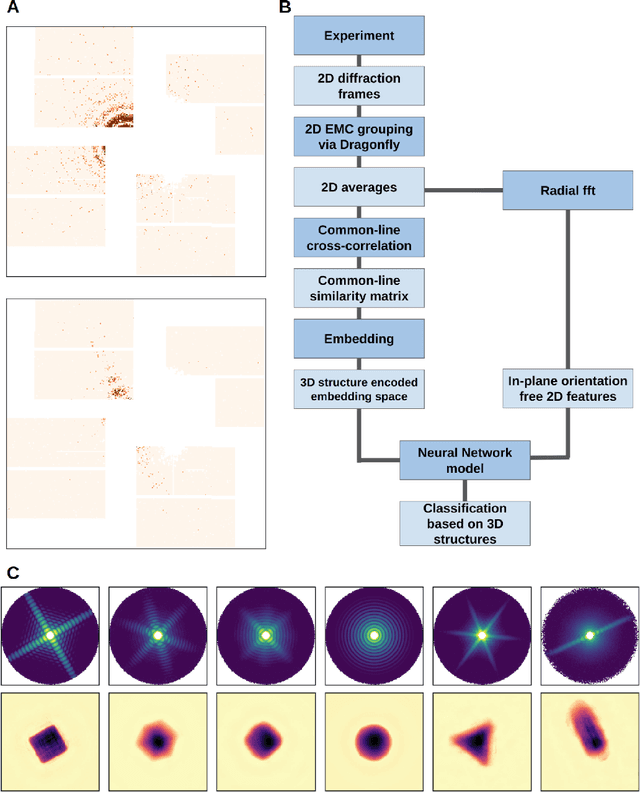
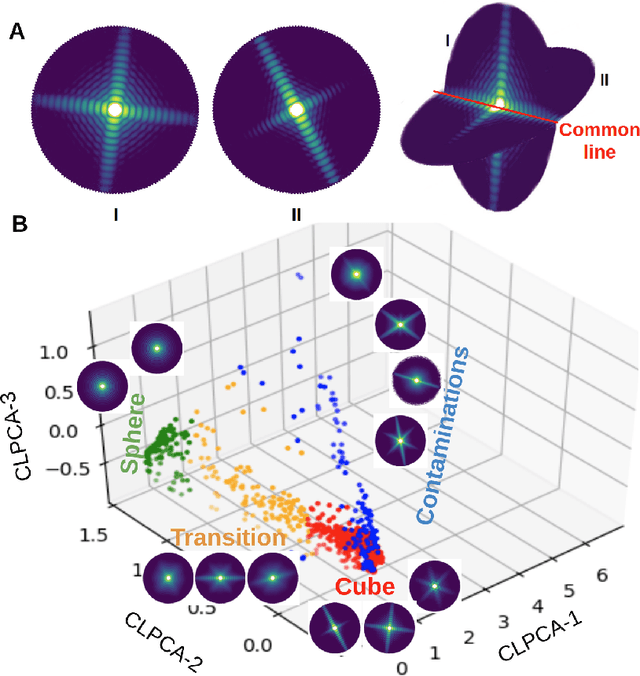
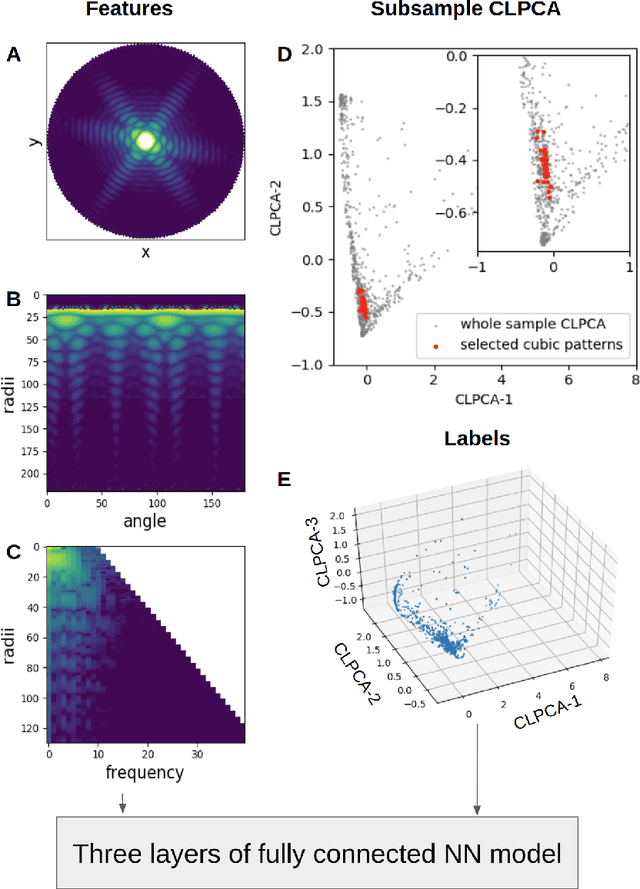
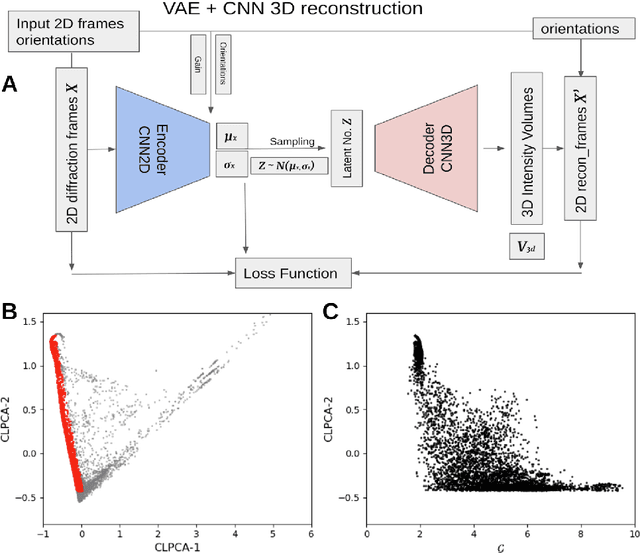
One of the outstanding analytical problems in X-ray single particle imaging (SPI) is the classification of structural heterogeneity, which is especially difficult given the low signal-to-noise ratios of individual patterns and that even identical objects can yield patterns that vary greatly when orientation is taken into consideration. We propose two methods which explicitly account for this orientation-induced variation and can robustly determine the structural landscape of a sample ensemble. The first, termed common-line principal component analysis (PCA) provides a rough classification which is essentially parameter-free and can be run automatically on any SPI dataset. The second method, utilizing variation auto-encoders (VAEs) can generate 3D structures of the objects at any point in the structural landscape. We implement both these methods in combination with the noise-tolerant expand-maximize-compress (EMC) algorithm and demonstrate its utility by applying it to an experimental dataset from gold nanoparticles with only a few thousand photons per pattern and recover both discrete structural classes as well as continuous deformations. These developments diverge from previous approaches of extracting reproducible subsets of patterns from a dataset and open up the possibility to move beyond studying homogeneous sample sets and study open questions on topics such as nanocrystal growth and dynamics as well as phase transitions which have not been externally triggered.