On the minimax optimality of Flow Matching through the connection to kernel density estimation

Flow Matching has recently gained attention in generative modeling as a simple and flexible alternative to diffusion models, the current state of the art. While existing statistical guarantees adapt tools from the analysis of diffusion models, we take a different perspective by connecting Flow Matching to kernel density estimation. We first verify that the kernel density estimator matches the optimal rate of convergence in Wasserstein distance up to logarithmic factors, improving existing bounds for the Gaussian kernel. Based on this result, we prove that for sufficiently large networks, Flow Matching also achieves the optimal rate up to logarithmic factors, providing a theoretical foundation for the empirical success of this method. Finally, we provide a first justification of Flow Matching's effectiveness in high-dimensional settings by showing that rates improve when the target distribution lies on a lower-dimensional linear subspace.

Calibrating Bayesian Generative Machine Learning for Bayesiamplification

Recently, combinations of generative and Bayesian machine learning have been introduced in particle physics for both fast detector simulation and inference tasks. These neural networks aim to quantify the uncertainty on the generated distribution originating from limited training statistics. The interpretation of a distribution-wide uncertainty however remains ill-defined. We show a clear scheme for quantifying the calibration of Bayesian generative machine learning models. For a Continuous Normalizing Flow applied to a low-dimensional toy example, we evaluate the calibration of Bayesian uncertainties from either a mean-field Gaussian weight posterior, or Monte Carlo sampling network weights, to gauge their behaviour on unsteady distribution edges. Well calibrated uncertainties can then be used to roughly estimate the number of uncorrelated truth samples that are equivalent to the generated sample and clearly indicate data amplification for smooth features of the distribution.

A Wasserstein perspective of Vanilla GANs

The empirical success of Generative Adversarial Networks (GANs) caused an increasing interest in theoretical research. The statistical literature is mainly focused on Wasserstein GANs and generalizations thereof, which especially allow for good dimension reduction properties. Statistical results for Vanilla GANs, the original optimization problem, are still rather limited and require assumptions such as smooth activation functions and equal dimensions of the latent space and the ambient space. To bridge this gap, we draw a connection from Vanilla GANs to the Wasserstein distance. By doing so, existing results for Wasserstein GANs can be extended to Vanilla GANs. In particular, we obtain an oracle inequality for Vanilla GANs in Wasserstein distance. The assumptions of this oracle inequality are designed to be satisfied by network architectures commonly used in practice, such as feedforward ReLU networks. By providing a quantitative result for the approximation of a Lipschitz function by a feedforward ReLU network with bounded H\"older norm, we conclude a rate of convergence for Vanilla GANs as well as Wasserstein GANs as estimators of the unknown probability distribution.

AdamMCMC: Combining Metropolis Adjusted Langevin with Momentum-based Optimization

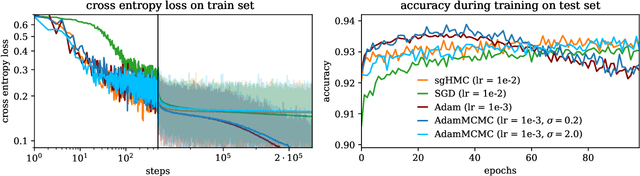
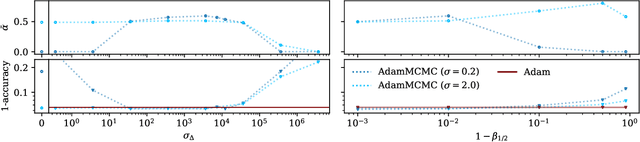
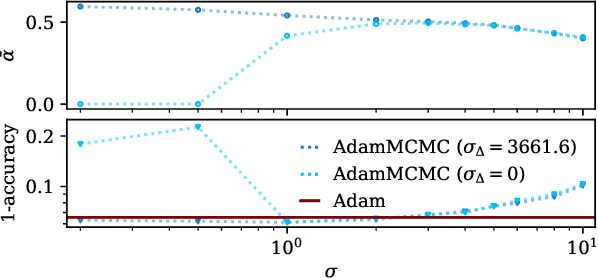
Uncertainty estimation is a key issue when considering the application of deep neural network methods in science and engineering. In this work, we introduce a novel algorithm that quantifies epistemic uncertainty via Monte Carlo sampling from a tempered posterior distribution. It combines the well established Metropolis Adjusted Langevin Algorithm (MALA) with momentum-based optimization using Adam and leverages a prolate proposal distribution, to efficiently draw from the posterior. We prove that the constructed chain admits the Gibbs posterior as an invariant distribution and converges to this Gibbs posterior in total variation distance. Numerical evaluations are postponed to a first revision.

Statistical guarantees for stochastic Metropolis-Hastings

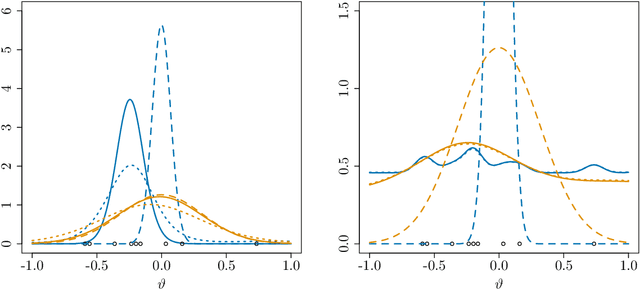
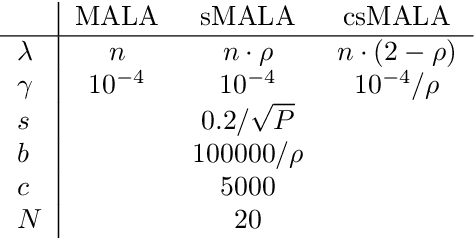
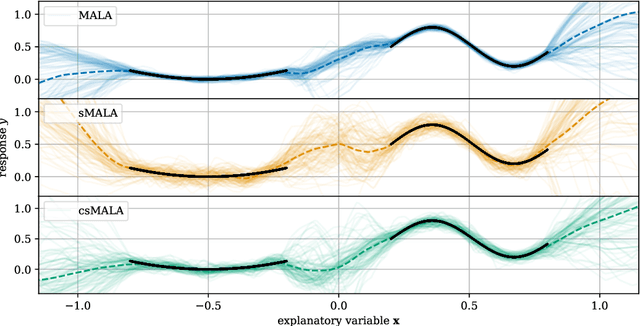
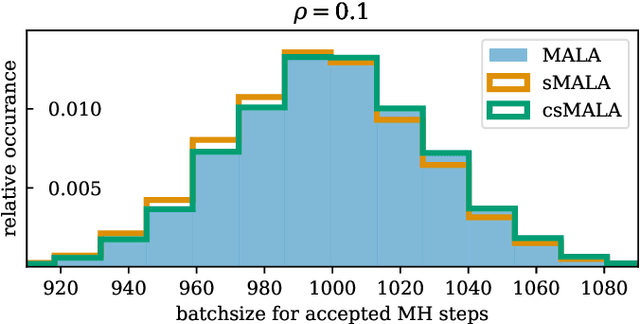
A Metropolis-Hastings step is widely used for gradient-based Markov chain Monte Carlo methods in uncertainty quantification. By calculating acceptance probabilities on batches, a stochastic Metropolis-Hastings step saves computational costs, but reduces the effective sample size. We show that this obstacle can be avoided by a simple correction term. We study statistical properties of the resulting stationary distribution of the chain if the corrected stochastic Metropolis-Hastings approach is applied to sample from a Gibbs posterior distribution in a nonparametric regression setting. Focusing on deep neural network regression, we prove a PAC-Bayes oracle inequality which yields optimal contraction rates and we analyze the diameter and show high coverage probability of the resulting credible sets. With a numerical example in a high-dimensional parameter space, we illustrate that credible sets and contraction rates of the stochastic Metropolis-Hastings algorithm indeed behave similar to those obtained from the classical Metropolis-adjusted Langevin algorithm.

PAC-Bayes training for neural networks: sparsity and uncertainty quantification

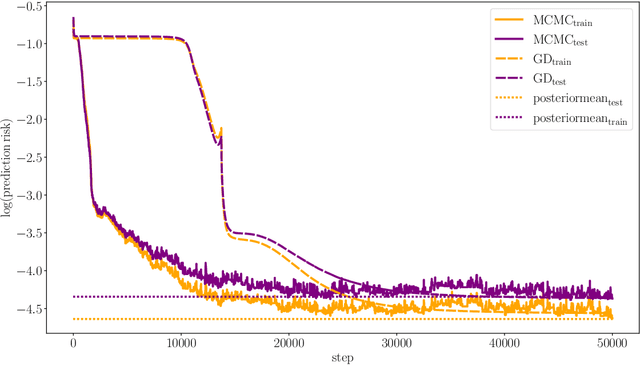
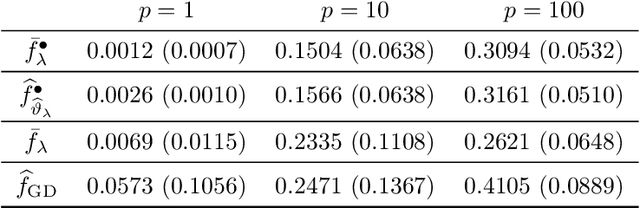
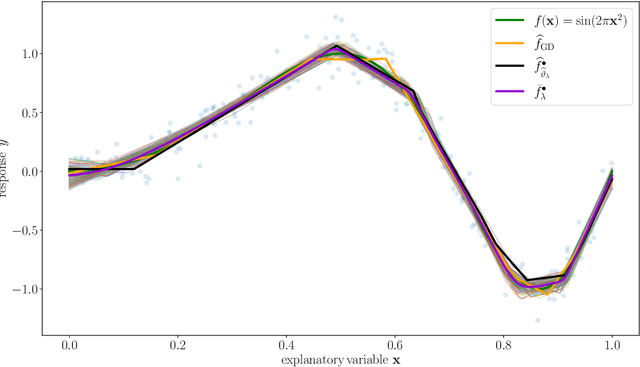
We study the Gibbs posterior distribution from PAC-Bayes theory for sparse deep neural nets in a nonparametric regression setting. To access the posterior distribution, an efficient MCMC algorithm based on backpropagation is constructed. The training yields a Bayesian neural network with a joint distribution on the network parameters. Using a mixture over uniform priors on sparse sets of networks weights, we prove an oracle inequality which shows that the method adapts to the unknown regularity and hierarchical structure of the regression function. Studying the Gibbs posterior distribution from a frequentist Bayesian perspective, we analyze the diameter and show high coverage probability of the resulting credible sets. The method is illustrated in a simulation example.

Dimensionality Reduction and Wasserstein Stability for Kernel Regression

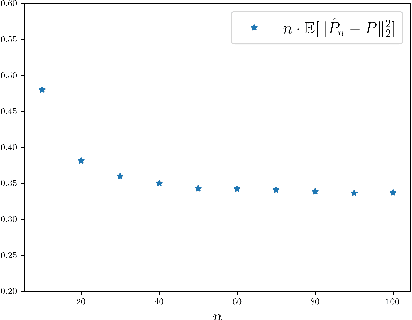
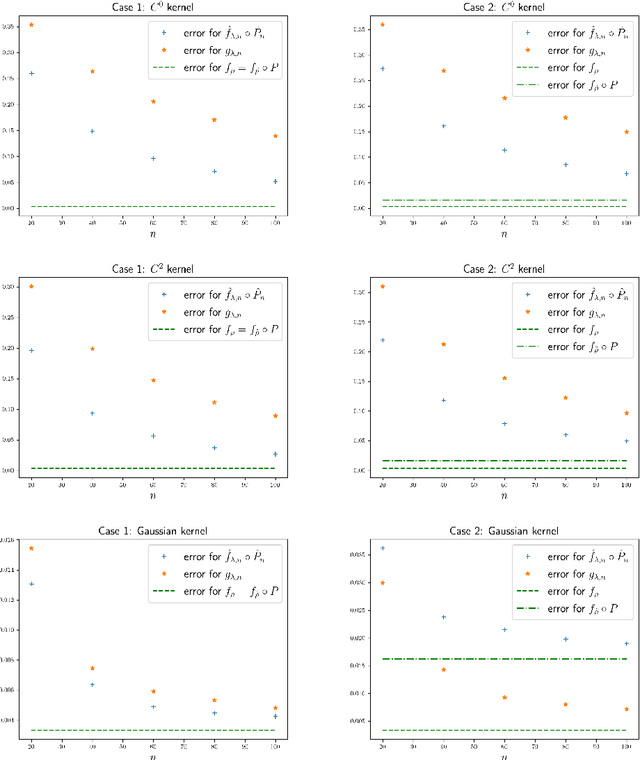
In a high-dimensional regression framework, we study consequences of the naive two-step procedure where first the dimension of the input variables is reduced and second, the reduced input variables are used to predict the output variable. More specifically we combine principal component analysis (PCA) with kernel regression. In order to analyze the resulting regression errors, a novel stability result of kernel regression with respect to the Wasserstein distance is derived. This allows us to bound errors that occur when perturbed input data is used to fit a kernel function. We combine the stability result with known estimates from the literature on both principal component analysis and kernel regression to obtain convergence rates for the two-step procedure.