AdamMCMC: Combining Metropolis Adjusted Langevin with Momentum-based Optimization

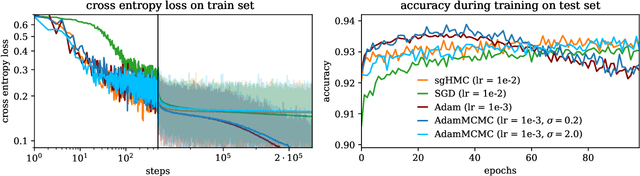
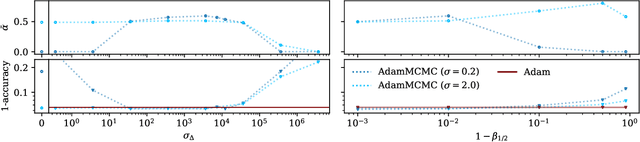
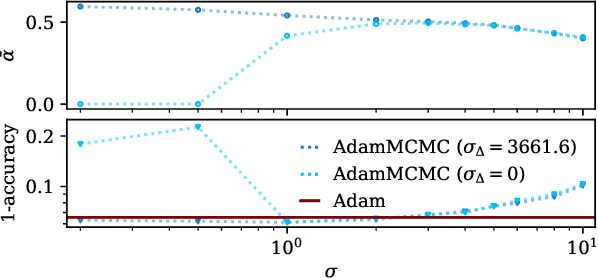
Uncertainty estimation is a key issue when considering the application of deep neural network methods in science and engineering. In this work, we introduce a novel algorithm that quantifies epistemic uncertainty via Monte Carlo sampling from a tempered posterior distribution. It combines the well established Metropolis Adjusted Langevin Algorithm (MALA) with momentum-based optimization using Adam and leverages a prolate proposal distribution, to efficiently draw from the posterior. We prove that the constructed chain admits the Gibbs posterior as an invariant distribution and converges to this Gibbs posterior in total variation distance. Numerical evaluations are postponed to a first revision.

Statistical guarantees for stochastic Metropolis-Hastings

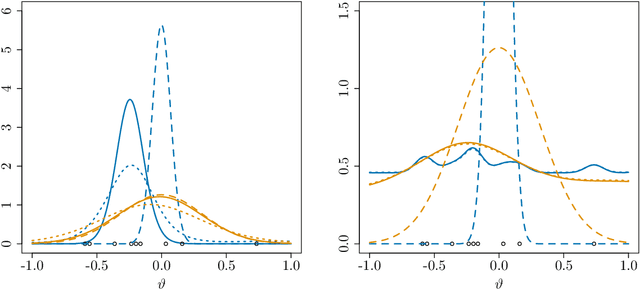
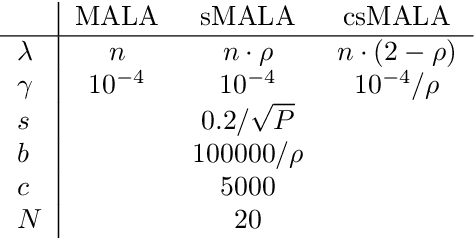
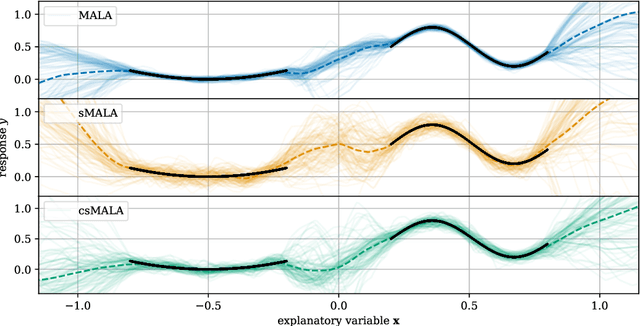
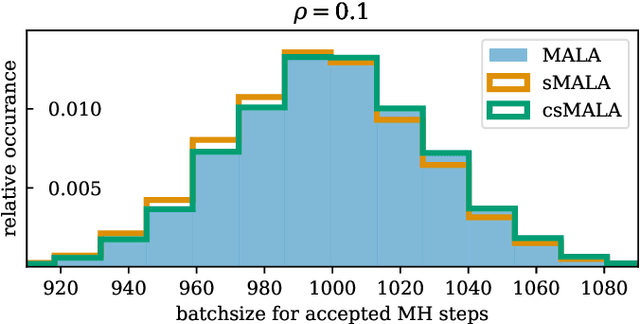
A Metropolis-Hastings step is widely used for gradient-based Markov chain Monte Carlo methods in uncertainty quantification. By calculating acceptance probabilities on batches, a stochastic Metropolis-Hastings step saves computational costs, but reduces the effective sample size. We show that this obstacle can be avoided by a simple correction term. We study statistical properties of the resulting stationary distribution of the chain if the corrected stochastic Metropolis-Hastings approach is applied to sample from a Gibbs posterior distribution in a nonparametric regression setting. Focusing on deep neural network regression, we prove a PAC-Bayes oracle inequality which yields optimal contraction rates and we analyze the diameter and show high coverage probability of the resulting credible sets. With a numerical example in a high-dimensional parameter space, we illustrate that credible sets and contraction rates of the stochastic Metropolis-Hastings algorithm indeed behave similar to those obtained from the classical Metropolis-adjusted Langevin algorithm.

PAC-Bayes training for neural networks: sparsity and uncertainty quantification

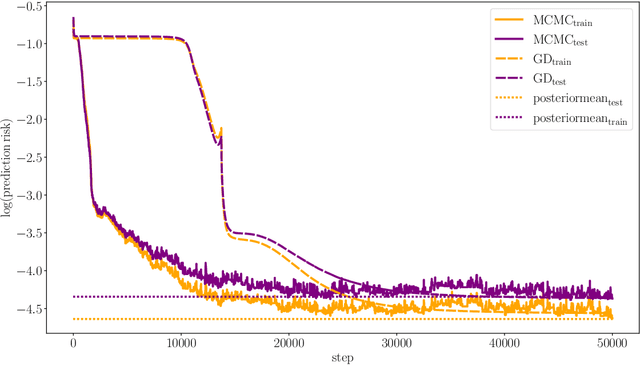
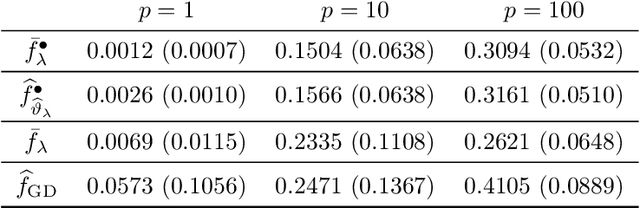
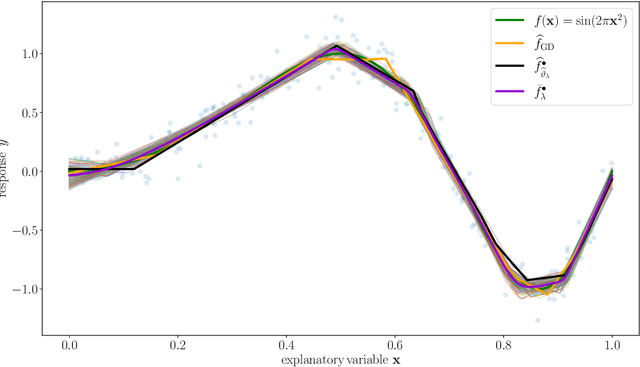
We study the Gibbs posterior distribution from PAC-Bayes theory for sparse deep neural nets in a nonparametric regression setting. To access the posterior distribution, an efficient MCMC algorithm based on backpropagation is constructed. The training yields a Bayesian neural network with a joint distribution on the network parameters. Using a mixture over uniform priors on sparse sets of networks weights, we prove an oracle inequality which shows that the method adapts to the unknown regularity and hierarchical structure of the regression function. Studying the Gibbs posterior distribution from a frequentist Bayesian perspective, we analyze the diameter and show high coverage probability of the resulting credible sets. The method is illustrated in a simulation example.