PAC-Bayes training for neural networks: sparsity and uncertainty quantification

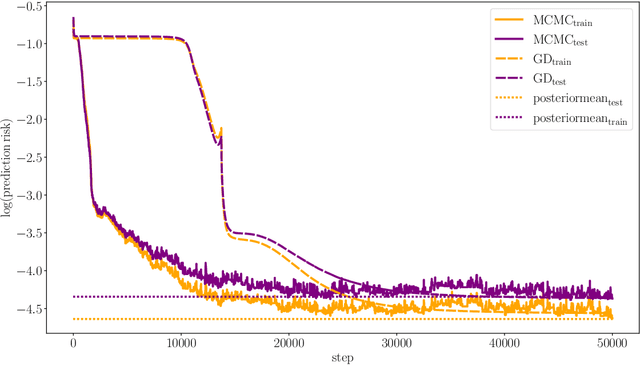
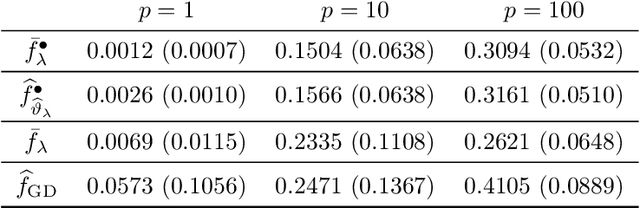
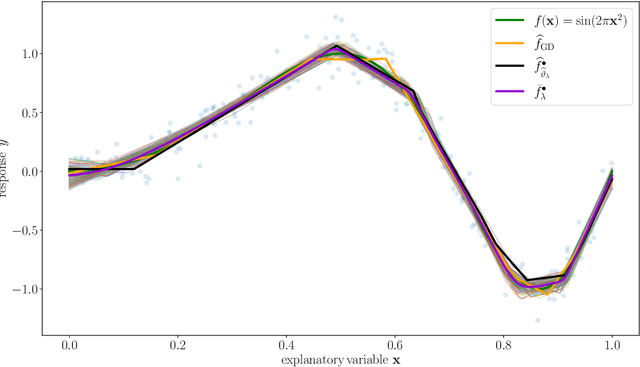
We study the Gibbs posterior distribution from PAC-Bayes theory for sparse deep neural nets in a nonparametric regression setting. To access the posterior distribution, an efficient MCMC algorithm based on backpropagation is constructed. The training yields a Bayesian neural network with a joint distribution on the network parameters. Using a mixture over uniform priors on sparse sets of networks weights, we prove an oracle inequality which shows that the method adapts to the unknown regularity and hierarchical structure of the regression function. Studying the Gibbs posterior distribution from a frequentist Bayesian perspective, we analyze the diameter and show high coverage probability of the resulting credible sets. The method is illustrated in a simulation example.