Calibrating Bayesian Generative Machine Learning for Bayesiamplification

Recently, combinations of generative and Bayesian machine learning have been introduced in particle physics for both fast detector simulation and inference tasks. These neural networks aim to quantify the uncertainty on the generated distribution originating from limited training statistics. The interpretation of a distribution-wide uncertainty however remains ill-defined. We show a clear scheme for quantifying the calibration of Bayesian generative machine learning models. For a Continuous Normalizing Flow applied to a low-dimensional toy example, we evaluate the calibration of Bayesian uncertainties from either a mean-field Gaussian weight posterior, or Monte Carlo sampling network weights, to gauge their behaviour on unsteady distribution edges. Well calibrated uncertainties can then be used to roughly estimate the number of uncorrelated truth samples that are equivalent to the generated sample and clearly indicate data amplification for smooth features of the distribution.

AdamMCMC: Combining Metropolis Adjusted Langevin with Momentum-based Optimization

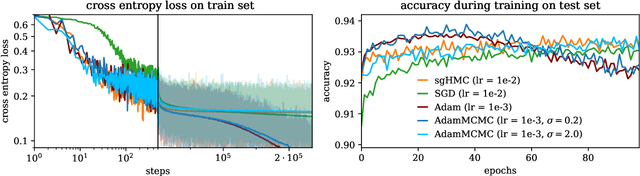
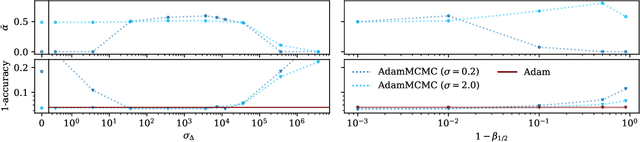
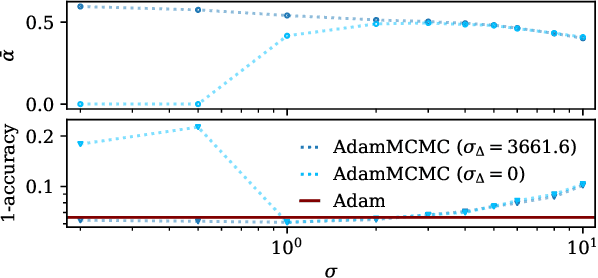
Uncertainty estimation is a key issue when considering the application of deep neural network methods in science and engineering. In this work, we introduce a novel algorithm that quantifies epistemic uncertainty via Monte Carlo sampling from a tempered posterior distribution. It combines the well established Metropolis Adjusted Langevin Algorithm (MALA) with momentum-based optimization using Adam and leverages a prolate proposal distribution, to efficiently draw from the posterior. We prove that the constructed chain admits the Gibbs posterior as an invariant distribution and converges to this Gibbs posterior in total variation distance. Numerical evaluations are postponed to a first revision.

Statistical guarantees for stochastic Metropolis-Hastings

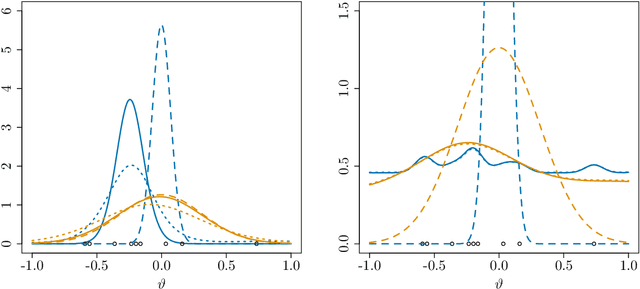
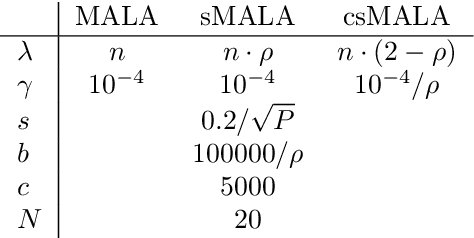
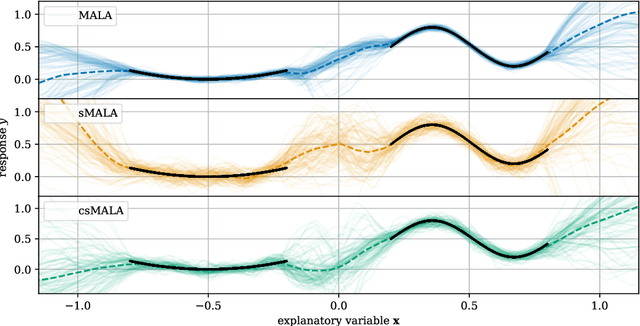
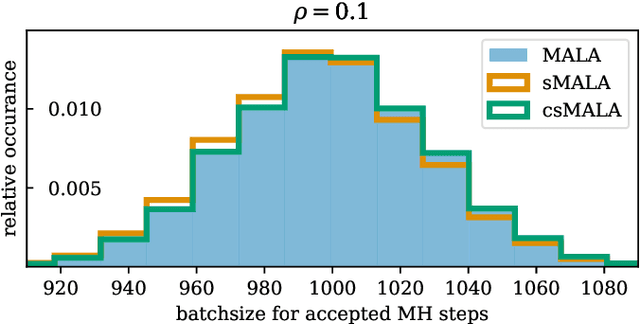
A Metropolis-Hastings step is widely used for gradient-based Markov chain Monte Carlo methods in uncertainty quantification. By calculating acceptance probabilities on batches, a stochastic Metropolis-Hastings step saves computational costs, but reduces the effective sample size. We show that this obstacle can be avoided by a simple correction term. We study statistical properties of the resulting stationary distribution of the chain if the corrected stochastic Metropolis-Hastings approach is applied to sample from a Gibbs posterior distribution in a nonparametric regression setting. Focusing on deep neural network regression, we prove a PAC-Bayes oracle inequality which yields optimal contraction rates and we analyze the diameter and show high coverage probability of the resulting credible sets. With a numerical example in a high-dimensional parameter space, we illustrate that credible sets and contraction rates of the stochastic Metropolis-Hastings algorithm indeed behave similar to those obtained from the classical Metropolis-adjusted Langevin algorithm.