Statistical guarantees for stochastic Metropolis-Hastings
Paper and Code
Oct 13, 2023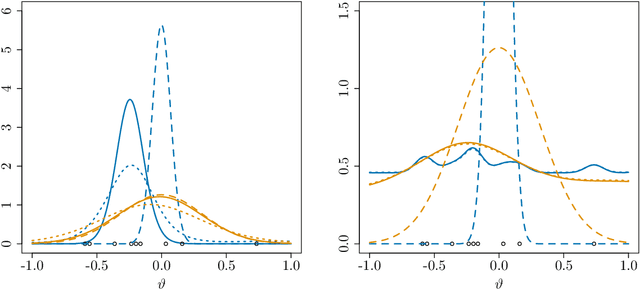
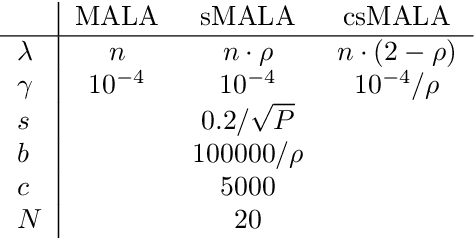
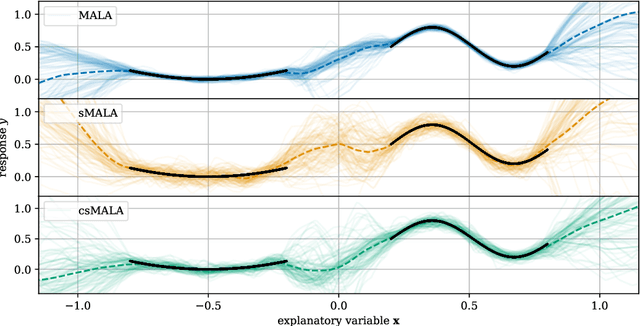
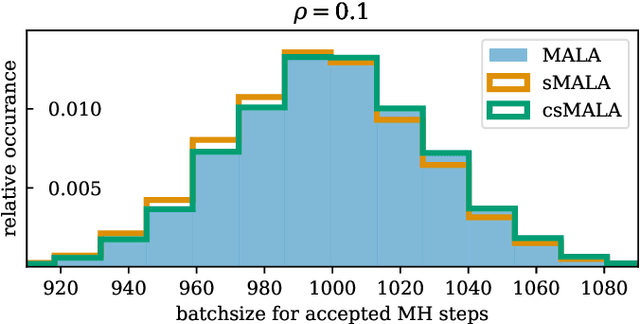
A Metropolis-Hastings step is widely used for gradient-based Markov chain Monte Carlo methods in uncertainty quantification. By calculating acceptance probabilities on batches, a stochastic Metropolis-Hastings step saves computational costs, but reduces the effective sample size. We show that this obstacle can be avoided by a simple correction term. We study statistical properties of the resulting stationary distribution of the chain if the corrected stochastic Metropolis-Hastings approach is applied to sample from a Gibbs posterior distribution in a nonparametric regression setting. Focusing on deep neural network regression, we prove a PAC-Bayes oracle inequality which yields optimal contraction rates and we analyze the diameter and show high coverage probability of the resulting credible sets. With a numerical example in a high-dimensional parameter space, we illustrate that credible sets and contraction rates of the stochastic Metropolis-Hastings algorithm indeed behave similar to those obtained from the classical Metropolis-adjusted Langevin algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge