Time-Causal VAE: Robust Financial Time Series Generator

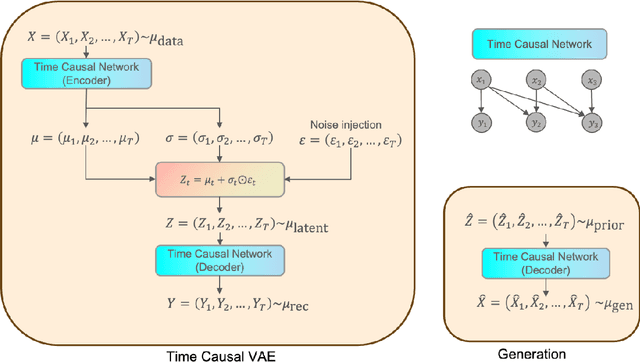
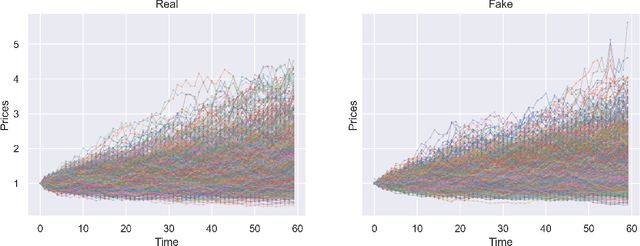
We build a time-causal variational autoencoder (TC-VAE) for robust generation of financial time series data. Our approach imposes a causality constraint on the encoder and decoder networks, ensuring a causal transport from the real market time series to the fake generated time series. Specifically, we prove that the TC-VAE loss provides an upper bound on the causal Wasserstein distance between market distributions and generated distributions. Consequently, the TC-VAE loss controls the discrepancy between optimal values of various dynamic stochastic optimization problems under real and generated distributions. To further enhance the model's ability to approximate the latent representation of the real market distribution, we integrate a RealNVP prior into the TC-VAE framework. Finally, extensive numerical experiments show that TC-VAE achieves promising results on both synthetic and real market data. This is done by comparing real and generated distributions according to various statistical distances, demonstrating the effectiveness of the generated data for downstream financial optimization tasks, as well as showcasing that the generated data reproduces stylized facts of real financial market data.

Hilbert's projective metric for functions of bounded growth and exponential convergence of Sinkhorn's algorithm

We study versions of Hilbert's projective metric for spaces of integrable functions of bounded growth. These metrics originate from cones which are relaxations of the cone of all non-negative functions, in the sense that they include all functions having non-negative integral values when multiplied with certain test functions. We show that kernel integral operators are contractions with respect to suitable specifications of such metrics even for kernels which are not bounded away from zero, provided that the decay to zero of the kernel is controlled. As an application to entropic optimal transport, we show exponential convergence of Sinkhorn's algorithm in settings where the marginal distributions have sufficiently light tails compared to the growth of the cost function.

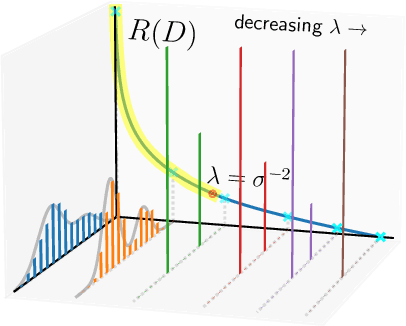
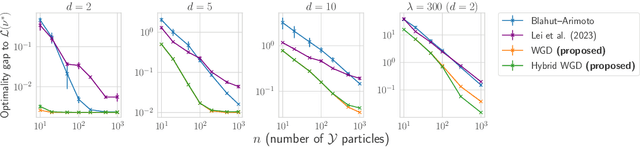
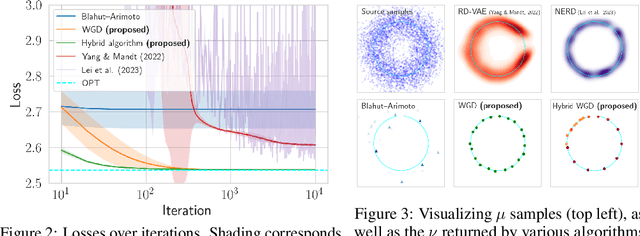
Estimating the Rate-Distortion Function by Wasserstein Gradient Descent

In the theory of lossy compression, the rate-distortion (R-D) function $R(D)$ describes how much a data source can be compressed (in bit-rate) at any given level of fidelity (distortion). Obtaining $R(D)$ for a given data source establishes the fundamental performance limit for all compression algorithms. We propose a new method to estimate $R(D)$ from the perspective of optimal transport. Unlike the classic Blahut--Arimoto algorithm which fixes the support of the reproduction distribution in advance, our Wasserstein gradient descent algorithm learns the support of the optimal reproduction distribution by moving particles. We prove its local convergence and analyze the sample complexity of our R-D estimator based on a connection to entropic optimal transport. Experimentally, we obtain comparable or tighter bounds than state-of-the-art neural network methods on low-rate sources while requiring considerably less tuning and computation effort. We also highlight a connection to maximum-likelihood deconvolution and introduce a new class of sources that can be used as test cases with known solutions to the R-D problem.

Convergence Rates for Regularized Optimal Transport via Quantization

We study the convergence of divergence-regularized optimal transport as the regularization parameter vanishes. Sharp rates for general divergences including relative entropy or $L^{p}$ regularization, general transport costs and multi-marginal problems are obtained. A novel methodology using quantization and martingale couplings is suitable for non-compact marginals and achieves, in particular, the sharp leading-order term of entropically regularized 2-Wasserstein distance for all marginals with finite $(2+\delta)$-moment.

Dimensionality Reduction and Wasserstein Stability for Kernel Regression

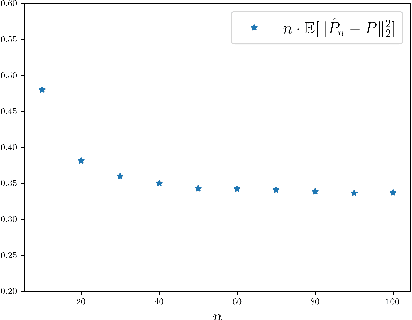
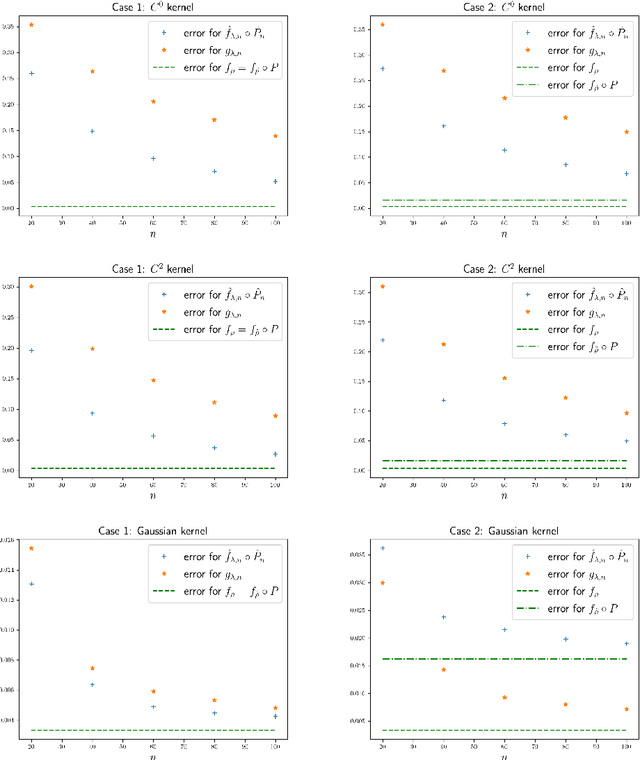
In a high-dimensional regression framework, we study consequences of the naive two-step procedure where first the dimension of the input variables is reduced and second, the reduced input variables are used to predict the output variable. More specifically we combine principal component analysis (PCA) with kernel regression. In order to analyze the resulting regression errors, a novel stability result of kernel regression with respect to the Wasserstein distance is derived. This allows us to bound errors that occur when perturbed input data is used to fit a kernel function. We combine the stability result with known estimates from the literature on both principal component analysis and kernel regression to obtain convergence rates for the two-step procedure.

MinMax Methods for Optimal Transport and Beyond: Regularization, Approximation and Numerics

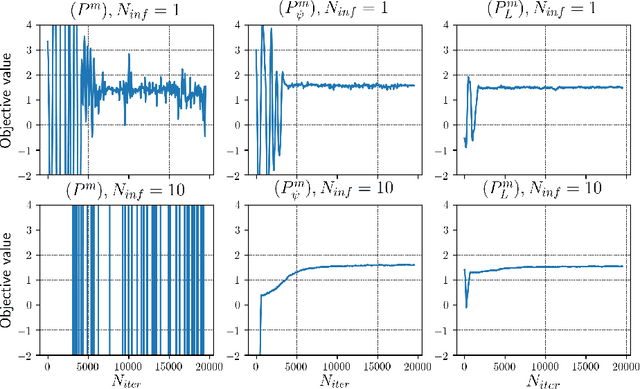
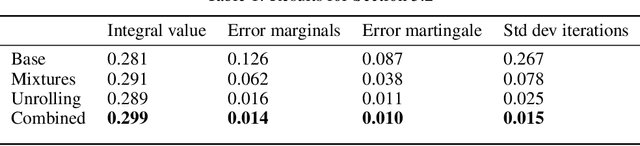
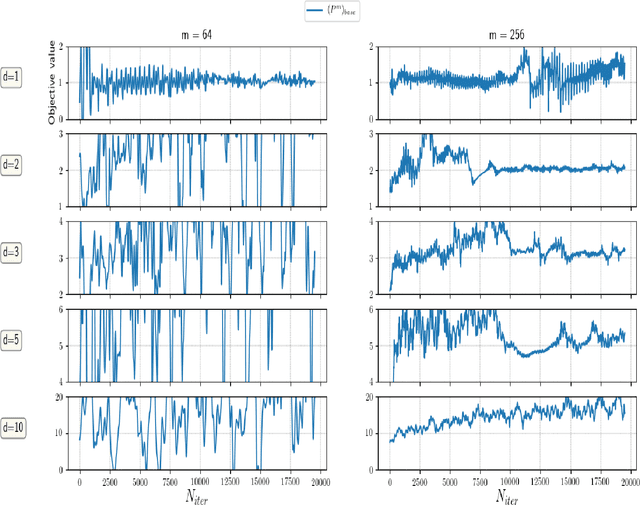
We study MinMax solution methods for a general class of optimization problems related to (and including) optimal transport. Theoretically, the focus is on fitting a large class of problems into a single MinMax framework and generalizing regularization techniques known from classical optimal transport. We show that regularization techniques justify the utilization of neural networks to solve such problems by proving approximation theorems and illustrating fundamental issues if no regularization is used. We further study the relation to the literature on generative adversarial nets, and analyze which algorithmic techniques used therein are particularly suitable to the class of problems studied in this paper. Several numerical experiments showcase the generality of the setting and highlight which theoretical insights are most beneficial in practice.

Lipschitz neural networks are dense in the set of all Lipschitz functions

This note shows that, for a fixed Lipschitz constant $L > 0$, one layer neural networks that are $L$-Lipschitz are dense in the set of all $L$-Lipschitz functions with respect to the uniform norm on bounded sets.

Computation of optimal transport and related hedging problems via penalization and neural networks

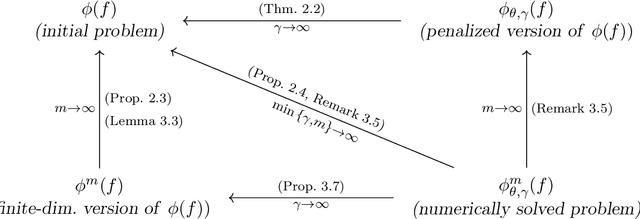
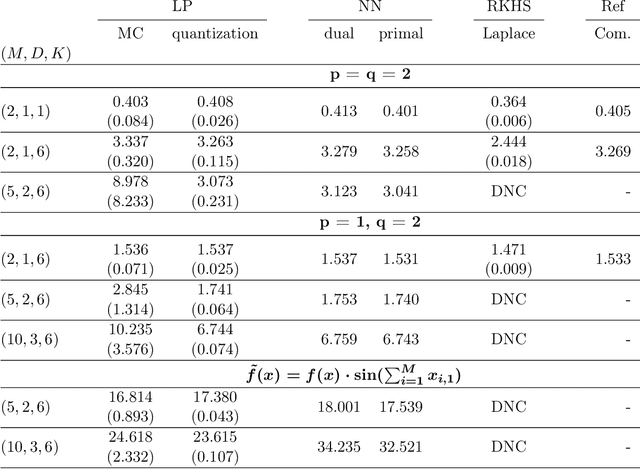
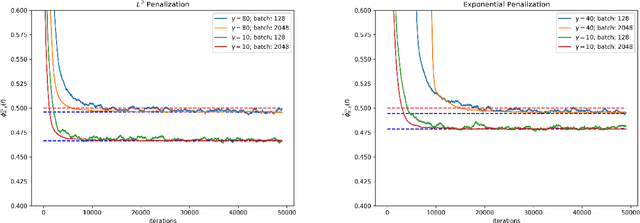
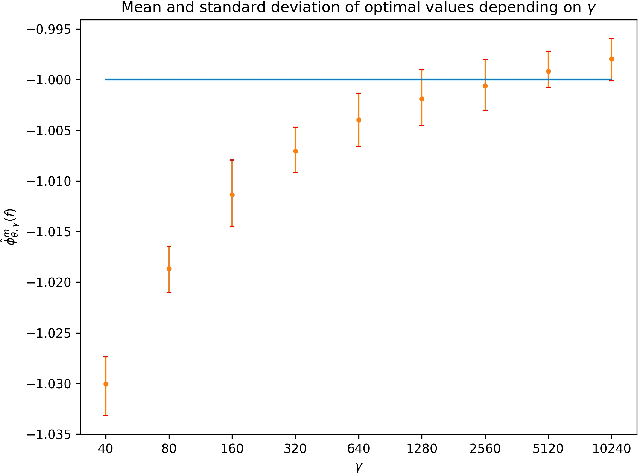
This paper presents a widely applicable approach to solving (multi-marginal, martingale) optimal transport and related problems via neural networks. The core idea is to penalize the optimization problem in its dual formulation and reduce it to a finite dimensional one which corresponds to optimizing a neural network with smooth objective function. We present numerical examples from optimal transport, martingale optimal transport, portfolio optimization under uncertainty and generative adversarial networks that showcase the generality and effectiveness of the approach.