Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Michael Kupper
Computation of optimal transport and related hedging problems via penalization and neural networks
Feb 23, 2018Figures and Tables: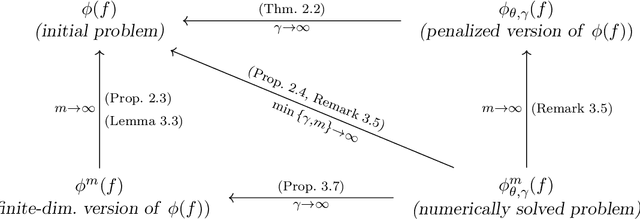
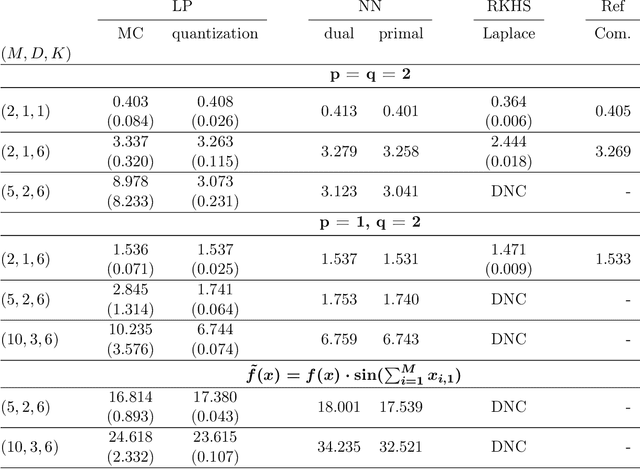
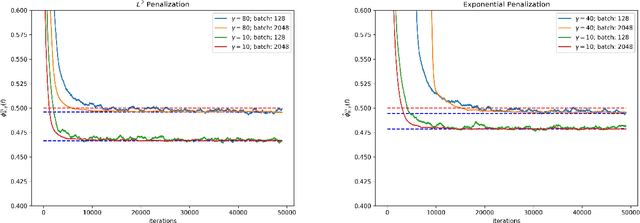
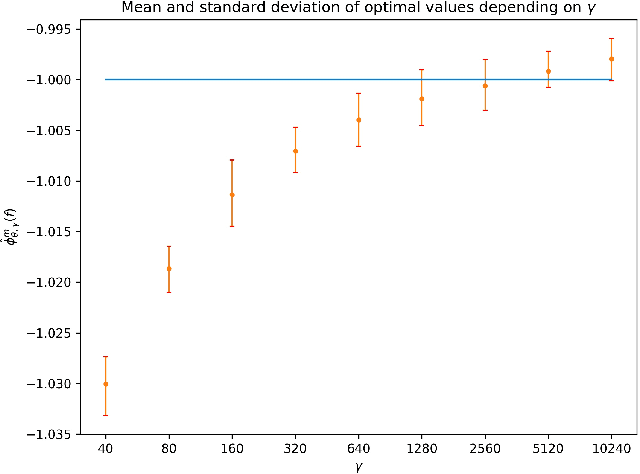




Abstract:This paper presents a widely applicable approach to solving (multi-marginal, martingale) optimal transport and related problems via neural networks. The core idea is to penalize the optimization problem in its dual formulation and reduce it to a finite dimensional one which corresponds to optimizing a neural network with smooth objective function. We present numerical examples from optimal transport, martingale optimal transport, portfolio optimization under uncertainty and generative adversarial networks that showcase the generality and effectiveness of the approach.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge