Parallel Token Prediction for Language Models

We propose Parallel Token Prediction (PTP), a universal framework for parallel sequence generation in language models. PTP jointly predicts multiple dependent tokens in a single transformer call by incorporating the sampling procedure into the model. This reduces the latency bottleneck of autoregressive decoding, and avoids the restrictive independence assumptions common in existing multi-token prediction methods. We prove that PTP can represent arbitrary autoregressive sequence distributions. PTP is trained either by distilling an existing model or through inverse autoregressive training without a teacher. Experimentally, we achieve state-of-the-art speculative decoding performance on Vicuna-7B by accepting over four tokens per step on Spec-Bench. The universality of our framework indicates that parallel generation of long sequences is feasible without loss of modeling power.

UMAMI: Unifying Masked Autoregressive Models and Deterministic Rendering for View Synthesis

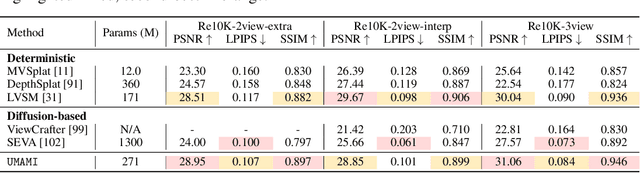
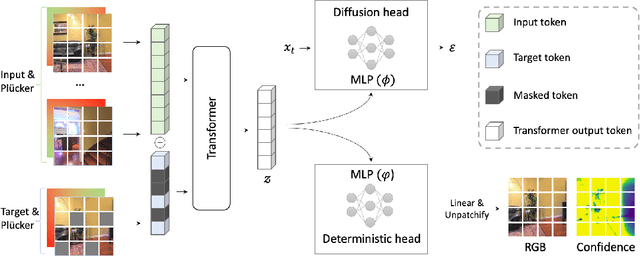
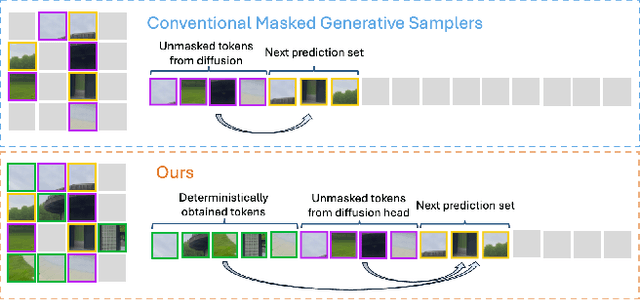
Novel view synthesis (NVS) seeks to render photorealistic, 3D-consistent images of a scene from unseen camera poses given only a sparse set of posed views. Existing deterministic networks render observed regions quickly but blur unobserved areas, whereas stochastic diffusion-based methods hallucinate plausible content yet incur heavy training- and inference-time costs. In this paper, we propose a hybrid framework that unifies the strengths of both paradigms. A bidirectional transformer encodes multi-view image tokens and Plucker-ray embeddings, producing a shared latent representation. Two lightweight heads then act on this representation: (i) a feed-forward regression head that renders pixels where geometry is well constrained, and (ii) a masked autoregressive diffusion head that completes occluded or unseen regions. The entire model is trained end-to-end with joint photometric and diffusion losses, without handcrafted 3D inductive biases, enabling scalability across diverse scenes. Experiments demonstrate that our method attains state-of-the-art image quality while reducing rendering time by an order of magnitude compared with fully generative baselines.

AstroCompress: A benchmark dataset for multi-purpose compression of astronomical data

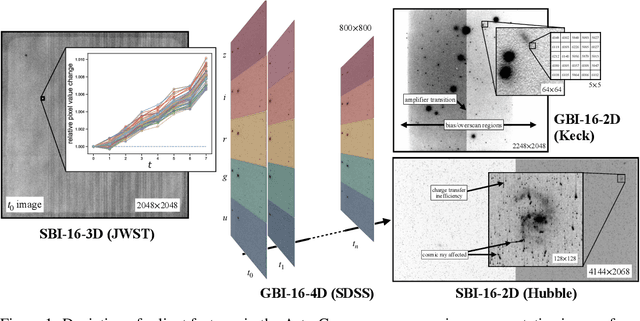
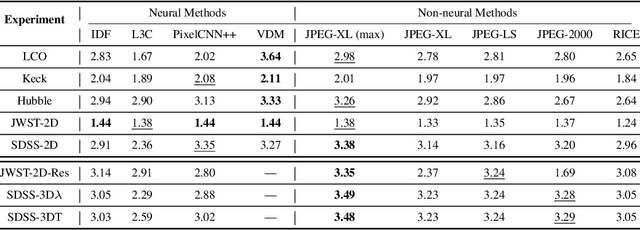
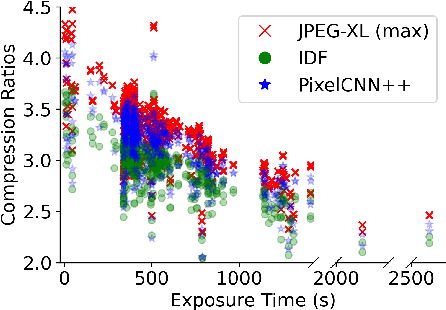
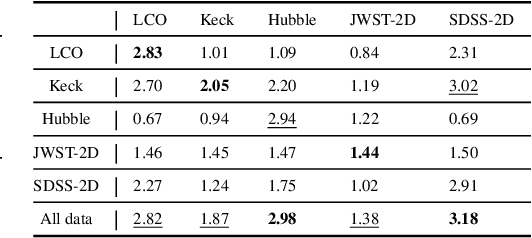
The site conditions that make astronomical observatories in space and on the ground so desirable -- cold and dark -- demand a physical remoteness that leads to limited data transmission capabilities. Such transmission limitations directly bottleneck the amount of data acquired and in an era of costly modern observatories, any improvements in lossless data compression has the potential scale to billions of dollars worth of additional science that can be accomplished on the same instrument. Traditional lossless methods for compressing astrophysical data are manually designed. Neural data compression, on the other hand, holds the promise of learning compression algorithms end-to-end from data and outperforming classical techniques by leveraging the unique spatial, temporal, and wavelength structures of astronomical images. This paper introduces AstroCompress: a neural compression challenge for astrophysics data, featuring four new datasets (and one legacy dataset) with 16-bit unsigned integer imaging data in various modes: space-based, ground-based, multi-wavelength, and time-series imaging. We provide code to easily access the data and benchmark seven lossless compression methods (three neural and four non-neural, including all practical state-of-the-art algorithms). Our results on lossless compression indicate that lossless neural compression techniques can enhance data collection at observatories, and provide guidance on the adoption of neural compression in scientific applications. Though the scope of this paper is restricted to lossless compression, we also comment on the potential exploration of lossy compression methods in future studies.

Diffusion-Guided Gaussian Splatting for Large-Scale Unconstrained 3D Reconstruction and Novel View Synthesis

Recent advancements in 3D Gaussian Splatting (3DGS) and Neural Radiance Fields (NeRF) have achieved impressive results in real-time 3D reconstruction and novel view synthesis. However, these methods struggle in large-scale, unconstrained environments where sparse and uneven input coverage, transient occlusions, appearance variability, and inconsistent camera settings lead to degraded quality. We propose GS-Diff, a novel 3DGS framework guided by a multi-view diffusion model to address these limitations. By generating pseudo-observations conditioned on multi-view inputs, our method transforms under-constrained 3D reconstruction problems into well-posed ones, enabling robust optimization even with sparse data. GS-Diff further integrates several enhancements, including appearance embedding, monocular depth priors, dynamic object modeling, anisotropy regularization, and advanced rasterization techniques, to tackle geometric and photometric challenges in real-world settings. Experiments on four benchmarks demonstrate that GS-Diff consistently outperforms state-of-the-art baselines by significant margins.

Generative Uncertainty in Diffusion Models

Diffusion models have recently driven significant breakthroughs in generative modeling. While state-of-the-art models produce high-quality samples on average, individual samples can still be low quality. Detecting such samples without human inspection remains a challenging task. To address this, we propose a Bayesian framework for estimating generative uncertainty of synthetic samples. We outline how to make Bayesian inference practical for large, modern generative models and introduce a new semantic likelihood (evaluated in the latent space of a feature extractor) to address the challenges posed by high-dimensional sample spaces. Through our experiments, we demonstrate that the proposed generative uncertainty effectively identifies poor-quality samples and significantly outperforms existing uncertainty-based methods. Notably, our Bayesian framework can be applied post-hoc to any pretrained diffusion or flow matching model (via the Laplace approximation), and we propose simple yet effective techniques to minimize its computational overhead during sampling.

Variational Control for Guidance in Diffusion Models

Diffusion models exhibit excellent sample quality, but existing guidance methods often require additional model training or are limited to specific tasks. We revisit guidance in diffusion models from the perspective of variational inference and control, introducing Diffusion Trajectory Matching (DTM) that enables guiding pretrained diffusion trajectories to satisfy a terminal cost. DTM unifies a broad class of guidance methods and enables novel instantiations. We introduce a new method within this framework that achieves state-of-the-art results on several linear and (blind) non-linear inverse problems without requiring additional model training or modifications. For instance, in ImageNet non-linear deblurring, our model achieves an FID score of 34.31, significantly improving over the best pretrained-method baseline (FID 78.07). We will make the code available in a future update.

Progressive Compression with Universally Quantized Diffusion Models

Diffusion probabilistic models have achieved mainstream success in many generative modeling tasks, from image generation to inverse problem solving. A distinct feature of these models is that they correspond to deep hierarchical latent variable models optimizing a variational evidence lower bound (ELBO) on the data likelihood. Drawing on a basic connection between likelihood modeling and compression, we explore the potential of diffusion models for progressive coding, resulting in a sequence of bits that can be incrementally transmitted and decoded with progressively improving reconstruction quality. Unlike prior work based on Gaussian diffusion or conditional diffusion models, we propose a new form of diffusion model with uniform noise in the forward process, whose negative ELBO corresponds to the end-to-end compression cost using universal quantization. We obtain promising first results on image compression, achieving competitive rate-distortion and rate-realism results on a wide range of bit-rates with a single model, bringing neural codecs a step closer to practical deployment.

One Diffusion to Generate Them All

We introduce OneDiffusion, a versatile, large-scale diffusion model that seamlessly supports bidirectional image synthesis and understanding across diverse tasks. It enables conditional generation from inputs such as text, depth, pose, layout, and semantic maps, while also handling tasks like image deblurring, upscaling, and reverse processes such as depth estimation and segmentation. Additionally, OneDiffusion allows for multi-view generation, camera pose estimation, and instant personalization using sequential image inputs. Our model takes a straightforward yet effective approach by treating all tasks as frame sequences with varying noise scales during training, allowing any frame to act as a conditioning image at inference time. Our unified training framework removes the need for specialized architectures, supports scalable multi-task training, and adapts smoothly to any resolution, enhancing both generalization and scalability. Experimental results demonstrate competitive performance across tasks in both generation and prediction such as text-to-image, multiview generation, ID preservation, depth estimation and camera pose estimation despite relatively small training dataset. Our code and checkpoint are freely available at https://github.com/lehduong/OneDiffusion

Weakly-Supervised Multimodal Learning on MIMIC-CXR

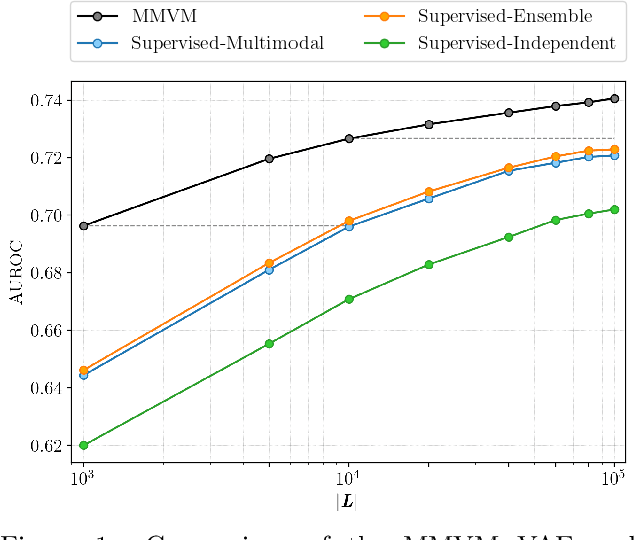
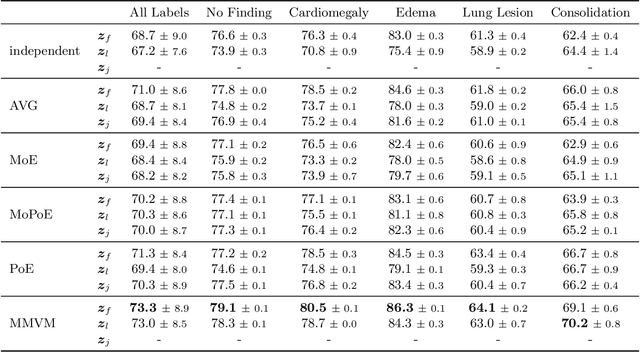
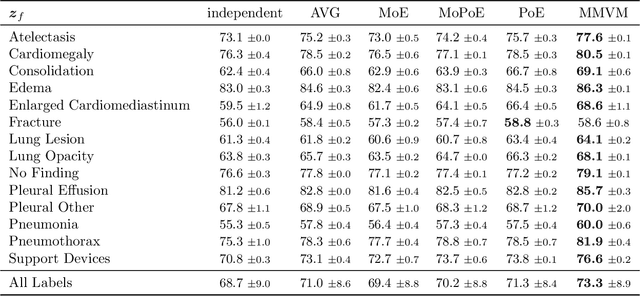
Multimodal data integration and label scarcity pose significant challenges for machine learning in medical settings. To address these issues, we conduct an in-depth evaluation of the newly proposed Multimodal Variational Mixture-of-Experts (MMVM) VAE on the challenging MIMIC-CXR dataset. Our analysis demonstrates that the MMVM VAE consistently outperforms other multimodal VAEs and fully supervised approaches, highlighting its strong potential for real-world medical applications.

Heavy-Tailed Diffusion Models

Diffusion models achieve state-of-the-art generation quality across many applications, but their ability to capture rare or extreme events in heavy-tailed distributions remains unclear. In this work, we show that traditional diffusion and flow-matching models with standard Gaussian priors fail to capture heavy-tailed behavior. We address this by repurposing the diffusion framework for heavy-tail estimation using multivariate Student-t distributions. We develop a tailored perturbation kernel and derive the denoising posterior based on the conditional Student-t distribution for the backward process. Inspired by $\gamma$-divergence for heavy-tailed distributions, we derive a training objective for heavy-tailed denoisers. The resulting framework introduces controllable tail generation using only a single scalar hyperparameter, making it easily tunable for diverse real-world distributions. As specific instantiations of our framework, we introduce t-EDM and t-Flow, extensions of existing diffusion and flow models that employ a Student-t prior. Remarkably, our approach is readily compatible with standard Gaussian diffusion models and requires only minimal code changes. Empirically, we show that our t-EDM and t-Flow outperform standard diffusion models in heavy-tail estimation on high-resolution weather datasets in which generating rare and extreme events is crucial.