Hierarchical Matrix Completion for the Prediction of Properties of Binary Mixtures

Predicting the thermodynamic properties of mixtures is crucial for process design and optimization in chemical engineering. Machine learning (ML) methods are gaining increasing attention in this field, but experimental data for training are often scarce, which hampers their application. In this work, we introduce a novel generic approach for improving data-driven models: inspired by the ancient rule "similia similibus solvuntur", we lump components that behave similarly into chemical classes and model them jointly in the first step of a hierarchical approach. While the information on class affiliations can stem in principle from any source, we demonstrate how classes can reproducibly be defined based on mixture data alone by agglomerative clustering. The information from this clustering step is then used as an informed prior for fitting the individual data. We demonstrate the benefits of this approach by applying it in connection with a matrix completion method (MCM) for predicting isothermal activity coefficients at infinite dilution in binary mixtures. Using clustering leads to significantly improved predictions compared to an MCM without clustering. Furthermore, the chemical classes learned from the clustering give exciting insights into what matters on the molecular level for modeling given mixture properties.

SetPINNs: Set-based Physics-informed Neural Networks

Physics-Informed Neural Networks (PINNs) have emerged as a promising method for approximating solutions to partial differential equations (PDEs) using deep learning. However, PINNs, based on multilayer perceptrons (MLP), often employ point-wise predictions, overlooking the implicit dependencies within the physical system such as temporal or spatial dependencies. These dependencies can be captured using more complex network architectures, for example CNNs or Transformers. However, these architectures conventionally do not allow for incorporating physical constraints, as advancements in integrating such constraints within these frameworks are still lacking. Relying on point-wise predictions often results in trivial solutions. To address this limitation, we propose SetPINNs, a novel approach inspired by Finite Elements Methods from the field of Numerical Analysis. SetPINNs allow for incorporating the dependencies inherent in the physical system while at the same time allowing for incorporating the physical constraints. They accurately approximate PDE solutions of a region, thereby modeling the inherent dependencies between multiple neighboring points in that region. Our experiments show that SetPINNs demonstrate superior generalization performance and accuracy across diverse physical systems, showing that they mitigate failure modes and converge faster in comparison to existing approaches. Furthermore, we demonstrate the utility of SetPINNs on two real-world physical systems.

HANNA: Hard-constraint Neural Network for Consistent Activity Coefficient Prediction

We present the first hard-constraint neural network for predicting activity coefficients (HANNA), a thermodynamic mixture property that is the basis for many applications in science and engineering. Unlike traditional neural networks, which ignore physical laws and result in inconsistent predictions, our model is designed to strictly adhere to all thermodynamic consistency criteria. By leveraging deep-set neural networks, HANNA maintains symmetry under the permutation of the components. Furthermore, by hard-coding physical constraints in the network architecture, we ensure consistency with the Gibbs-Duhem equation and in modeling the pure components. The model was trained and evaluated on 317,421 data points for activity coefficients in binary mixtures from the Dortmund Data Bank, achieving significantly higher prediction accuracies than the current state-of-the-art model UNIFAC. Moreover, HANNA only requires the SMILES of the components as input, making it applicable to any binary mixture of interest. HANNA is fully open-source and available for free use.

Balancing Molecular Information and Empirical Data in the Prediction of Physico-Chemical Properties

Predicting the physico-chemical properties of pure substances and mixtures is a central task in thermodynamics. Established prediction methods range from fully physics-based ab-initio calculations, which are only feasible for very simple systems, over descriptor-based methods that use some information on the molecules to be modeled together with fitted model parameters (e.g., quantitative-structure-property relationship methods or classical group contribution methods), to representation-learning methods, which may, in extreme cases, completely ignore molecular descriptors and extrapolate only from existing data on the property to be modeled (e.g., matrix completion methods). In this work, we propose a general method for combining molecular descriptors with representation learning using the so-called expectation maximization algorithm from the probabilistic machine learning literature, which uses uncertainty estimates to trade off between the two approaches. The proposed hybrid model exploits chemical structure information using graph neural networks, but it automatically detects cases where structure-based predictions are unreliable, in which case it corrects them by representation-learning based predictions that can better specialize to unusual cases. The effectiveness of the proposed method is demonstrated using the prediction of activity coefficients in binary mixtures as an example. The results are compelling, as the method significantly improves predictive accuracy over the current state of the art, showcasing its potential to advance the prediction of physico-chemical properties in general.

Deep Anomaly Detection on Tennessee Eastman Process Data

This paper provides the first comprehensive evaluation and analysis of modern (deep-learning) unsupervised anomaly detection methods for chemical process data. We focus on the Tennessee Eastman process dataset, which has been a standard litmus test to benchmark anomaly detection methods for nearly three decades. Our extensive study will facilitate choosing appropriate anomaly detection methods in industrial applications.

Hybridizing Physical and Data-driven Prediction Methods for Physicochemical Properties

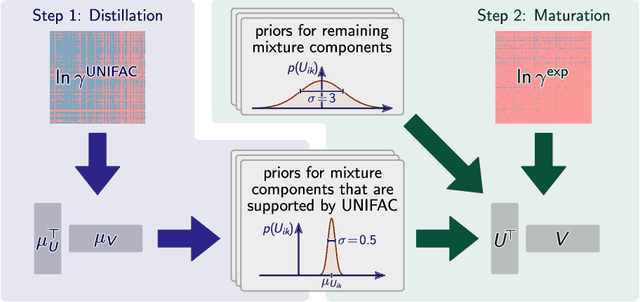
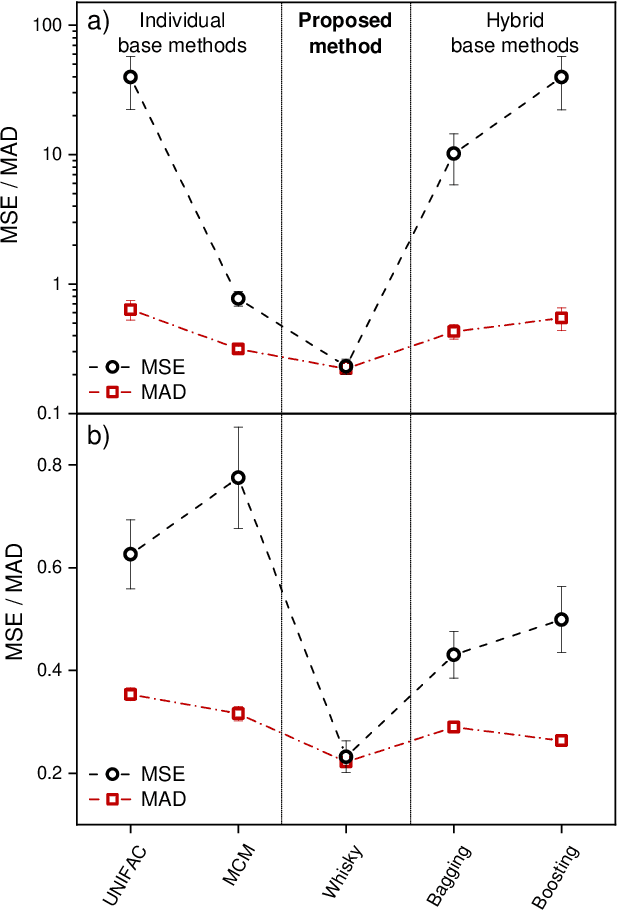
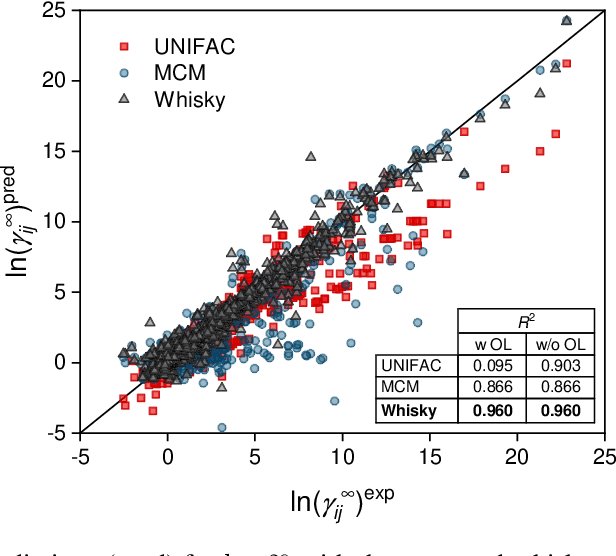
We present a generic way to hybridize physical and data-driven methods for predicting physicochemical properties. The approach `distills' the physical method's predictions into a prior model and combines it with sparse experimental data using Bayesian inference. We apply the new approach to predict activity coefficients at infinite dilution and obtain significant improvements compared to the data-driven and physical baselines and established ensemble methods from the machine learning literature.

Attribute-based Explanations of Non-Linear Embeddings of High-Dimensional Data

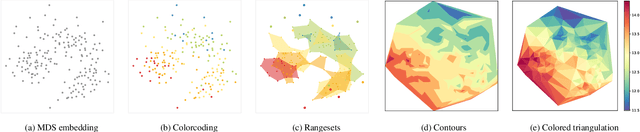
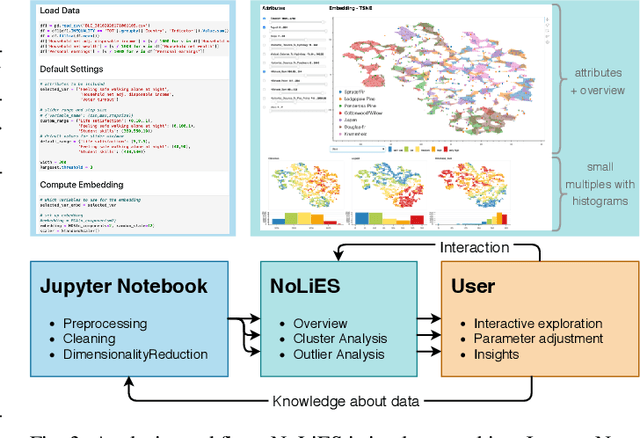
Embeddings of high-dimensional data are widely used to explore data, to verify analysis results, and to communicate information. Their explanation, in particular with respect to the input attributes, is often difficult. With linear projects like PCA the axes can still be annotated meaningfully. With non-linear projections this is no longer possible and alternative strategies such as attribute-based color coding are required. In this paper, we review existing augmentation techniques and discuss their limitations. We present the Non-Linear Embeddings Surveyor (NoLiES) that combines a novel augmentation strategy for projected data (rangesets) with interactive analysis in a small multiples setting. Rangesets use a set-based visualization approach for binned attribute values that enable the user to quickly observe structure and detect outliers. We detail the link between algebraic topology and rangesets and demonstrate the utility of NoLiES in case studies with various challenges (complex attribute value distribution, many attributes, many data points) and a real-world application to understand latent features of matrix completion in thermodynamics.

Machine Learning in Thermodynamics: Prediction of Activity Coefficients by Matrix Completion

Activity coefficients, which are a measure of the non-ideality of liquid mixtures, are a key property in chemical engineering with relevance to modeling chemical and phase equilibria as well as transport processes. Although experimental data on thousands of binary mixtures are available, prediction methods are needed to calculate the activity coefficients in many relevant mixtures that have not been explored to-date. In this report, we propose a probabilistic matrix factorization model for predicting the activity coefficients in arbitrary binary mixtures. Although no physical descriptors for the considered components were used, our method outperforms the state-of-the-art method that has been refined over three decades while requiring much less training effort. This opens perspectives to novel methods for predicting physico-chemical properties of binary mixtures with the potential to revolutionize modeling and simulation in chemical engineering.