Flipping Against All Odds: Reducing LLM Coin Flip Bias via Verbalized Rejection Sampling

Large language models (LLMs) can often accurately describe probability distributions using natural language, yet they still struggle to generate faithful samples from them. This mismatch limits their use in tasks requiring reliable stochasticity, such as Monte Carlo methods, agent-based simulations, and randomized decision-making. We investigate this gap between knowledge and sampling in the context of Bernoulli distributions. We introduce Verbalized Rejection Sampling (VRS), a natural-language adaptation of classical rejection sampling that prompts the LLM to reason about and accept or reject proposed samples. Despite relying on the same Bernoulli mechanism internally, VRS substantially reduces sampling bias across models. We provide theoretical analysis showing that, under mild assumptions, VRS improves over direct sampling, with gains attributable to both the algorithm and prompt design. More broadly, our results show how classical probabilistic tools can be verbalized and embedded into LLM workflows to improve reliability, without requiring access to model internals or heavy prompt engineering.

Reducing Storage of Pretrained Neural Networks by Rate-Constrained Quantization and Entropy Coding

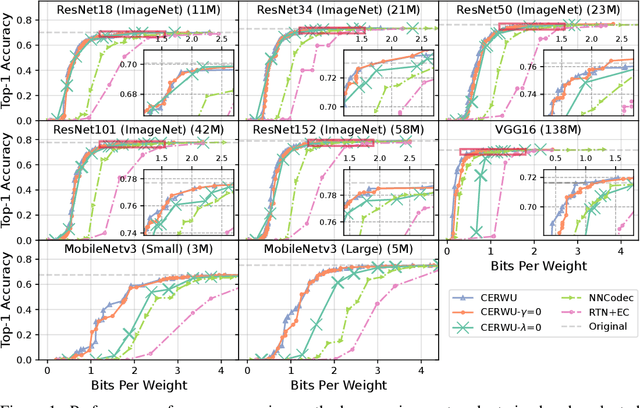
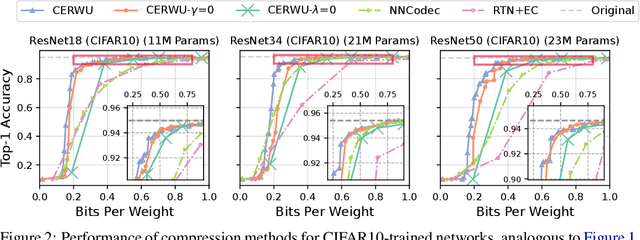
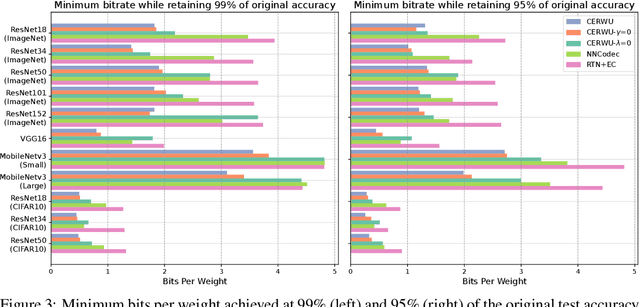
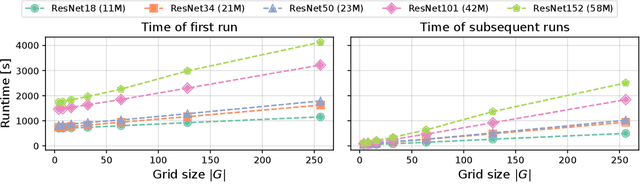
The ever-growing size of neural networks poses serious challenges on resource-constrained devices, such as embedded sensors. Compression algorithms that reduce their size can mitigate these problems, provided that model performance stays close to the original. We propose a novel post-training compression framework that combines rate-aware quantization with entropy coding by (1) extending the well-known layer-wise loss by a quadratic rate estimation, and (2) providing locally exact solutions to this modified objective following the Optimal Brain Surgeon (OBS) method. Our method allows for very fast decoding and is compatible with arbitrary quantization grids. We verify our results empirically by testing on various computer-vision networks, achieving a 20-40\% decrease in bit rate at the same performance as the popular compression algorithm NNCodec. Our code is available at https://github.com/Conzel/cerwu.

FSP-Laplace: Function-Space Priors for the Laplace Approximation in Bayesian Deep Learning

Laplace approximations are popular techniques for endowing deep networks with epistemic uncertainty estimates as they can be applied without altering the predictions of the neural network, and they scale to large models and datasets. While the choice of prior strongly affects the resulting posterior distribution, computational tractability and lack of interpretability of weight space typically limit the Laplace approximation to isotropic Gaussian priors, which are known to cause pathological behavior as depth increases. As a remedy, we directly place a prior on function space. More precisely, since Lebesgue densities do not exist on infinite-dimensional function spaces, we have to recast training as finding the so-called weak mode of the posterior measure under a Gaussian process (GP) prior restricted to the space of functions representable by the neural network. Through the GP prior, one can express structured and interpretable inductive biases, such as regularity or periodicity, directly in function space, while still exploiting the implicit inductive biases that allow deep networks to generalize. After model linearization, the training objective induces a negative log-posterior density to which we apply a Laplace approximation, leveraging highly scalable methods from matrix-free linear algebra. Our method provides improved results where prior knowledge is abundant, e.g., in many scientific inference tasks. At the same time, it stays competitive for black-box regression and classification tasks where neural networks typically excel.

Balancing Molecular Information and Empirical Data in the Prediction of Physico-Chemical Properties

Predicting the physico-chemical properties of pure substances and mixtures is a central task in thermodynamics. Established prediction methods range from fully physics-based ab-initio calculations, which are only feasible for very simple systems, over descriptor-based methods that use some information on the molecules to be modeled together with fitted model parameters (e.g., quantitative-structure-property relationship methods or classical group contribution methods), to representation-learning methods, which may, in extreme cases, completely ignore molecular descriptors and extrapolate only from existing data on the property to be modeled (e.g., matrix completion methods). In this work, we propose a general method for combining molecular descriptors with representation learning using the so-called expectation maximization algorithm from the probabilistic machine learning literature, which uses uncertainty estimates to trade off between the two approaches. The proposed hybrid model exploits chemical structure information using graph neural networks, but it automatically detects cases where structure-based predictions are unreliable, in which case it corrects them by representation-learning based predictions that can better specialize to unusual cases. The effectiveness of the proposed method is demonstrated using the prediction of activity coefficients in binary mixtures as an example. The results are compelling, as the method significantly improves predictive accuracy over the current state of the art, showcasing its potential to advance the prediction of physico-chemical properties in general.

Regularized KL-Divergence for Well-Defined Function-Space Variational Inference in Bayesian neural networks

Bayesian neural networks (BNN) promise to combine the predictive performance of neural networks with principled uncertainty modeling important for safety-critical systems and decision making. However, posterior uncertainty estimates depend on the choice of prior, and finding informative priors in weight-space has proven difficult. This has motivated variational inference (VI) methods that pose priors directly on the function generated by the BNN rather than on weights. In this paper, we address a fundamental issue with such function-space VI approaches pointed out by Burt et al. (2020), who showed that the objective function (ELBO) is negative infinite for most priors of interest. Our solution builds on generalized VI (Knoblauch et al., 2019) with the regularized KL divergence (Quang, 2019) and is, to the best of our knowledge, the first well-defined variational objective for function-space inference in BNNs with Gaussian process (GP) priors. Experiments show that our method incorporates the properties specified by the GP prior on synthetic and small real-world data sets, and provides competitive uncertainty estimates for regression, classification and out-of-distribution detection compared to BNN baselines with both function and weight-space priors.

Verbalized Machine Learning: Revisiting Machine Learning with Language Models

Motivated by the large progress made by large language models (LLMs), we introduce the framework of verbalized machine learning (VML). In contrast to conventional machine learning models that are typically optimized over a continuous parameter space, VML constrains the parameter space to be human-interpretable natural language. Such a constraint leads to a new perspective of function approximation, where an LLM with a text prompt can be viewed as a function parameterized by the text prompt. Guided by this perspective, we revisit classical machine learning problems, such as regression and classification, and find that these problems can be solved by an LLM-parameterized learner and optimizer. The major advantages of VML include (1) easy encoding of inductive bias: prior knowledge about the problem and hypothesis class can be encoded in natural language and fed into the LLM-parameterized learner; (2) automatic model class selection: the optimizer can automatically select a concrete model class based on data and verbalized prior knowledge, and it can update the model class during training; and (3) interpretable learner updates: the LLM-parameterized optimizer can provide explanations for why each learner update is performed. We conduct several studies to empirically evaluate the effectiveness of VML, and hope that VML can serve as a stepping stone to stronger interpretability and trustworthiness in ML.

Your Finetuned Large Language Model is Already a Powerful Out-of-distribution Detector

We revisit the likelihood ratio between a pretrained large language model (LLM) and its finetuned variant as a criterion for out-of-distribution (OOD) detection. The intuition behind such a criterion is that, the pretrained LLM has the prior knowledge about OOD data due to its large amount of training data, and once finetuned with the in-distribution data, the LLM has sufficient knowledge to distinguish their difference. Leveraging the power of LLMs, we show that, for the first time, the likelihood ratio can serve as an effective OOD detector. Moreover, we apply the proposed LLM-based likelihood ratio to detect OOD questions in question-answering (QA) systems, which can be used to improve the performance of specialized LLMs for general questions. Given that likelihood can be easily obtained by the loss functions within contemporary neural network frameworks, it is straightforward to implement this approach in practice. Since both the pretrained LLMs and its various finetuned models are available, our proposed criterion can be effortlessly incorporated for OOD detection without the need for further training. We conduct comprehensive evaluation across on multiple settings, including far OOD, near OOD, spam detection, and QA scenarios, to demonstrate the effectiveness of the method.

Predictive, scalable and interpretable knowledge tracing on structured domains

Intelligent tutoring systems optimize the selection and timing of learning materials to enhance understanding and long-term retention. This requires estimates of both the learner's progress (''knowledge tracing''; KT), and the prerequisite structure of the learning domain (''knowledge mapping''). While recent deep learning models achieve high KT accuracy, they do so at the expense of the interpretability of psychologically-inspired models. In this work, we present a solution to this trade-off. PSI-KT is a hierarchical generative approach that explicitly models how both individual cognitive traits and the prerequisite structure of knowledge influence learning dynamics, thus achieving interpretability by design. Moreover, by using scalable Bayesian inference, PSI-KT targets the real-world need for efficient personalization even with a growing body of learners and learning histories. Evaluated on three datasets from online learning platforms, PSI-KT achieves superior multi-step predictive accuracy and scalable inference in continual-learning settings, all while providing interpretable representations of learner-specific traits and the prerequisite structure of knowledge that causally supports learning. In sum, predictive, scalable and interpretable knowledge tracing with solid knowledge mapping lays a key foundation for effective personalized learning to make education accessible to a broad, global audience.

On the Challenges and Opportunities in Generative AI

The field of deep generative modeling has grown rapidly and consistently over the years. With the availability of massive amounts of training data coupled with advances in scalable unsupervised learning paradigms, recent large-scale generative models show tremendous promise in synthesizing high-resolution images and text, as well as structured data such as videos and molecules. However, we argue that current large-scale generative AI models do not sufficiently address several fundamental issues that hinder their widespread adoption across domains. In this work, we aim to identify key unresolved challenges in modern generative AI paradigms that should be tackled to further enhance their capabilities, versatility, and reliability. By identifying these challenges, we aim to provide researchers with valuable insights for exploring fruitful research directions, thereby fostering the development of more robust and accessible generative AI solutions.

A Compact Representation for Bayesian Neural Networks By Removing Permutation Symmetry

Bayesian neural networks (BNNs) are a principled approach to modeling predictive uncertainties in deep learning, which are important in safety-critical applications. Since exact Bayesian inference over the weights in a BNN is intractable, various approximate inference methods exist, among which sampling methods such as Hamiltonian Monte Carlo (HMC) are often considered the gold standard. While HMC provides high-quality samples, it lacks interpretable summary statistics because its sample mean and variance is meaningless in neural networks due to permutation symmetry. In this paper, we first show that the role of permutations can be meaningfully quantified by a number of transpositions metric. We then show that the recently proposed rebasin method allows us to summarize HMC samples into a compact representation that provides a meaningful explicit uncertainty estimate for each weight in a neural network, thus unifying sampling methods with variational inference. We show that this compact representation allows us to compare trained BNNs directly in weight space across sampling methods and variational inference, and to efficiently prune neural networks trained without explicit Bayesian frameworks by exploiting uncertainty estimates from HMC.